Benützer:


Beispiele für elektrische Felder
Storyboard

Abhängig von der Geometrie der Ladungsverteilung werden unterschiedliche elektrische Felder erhalten.

>Modell

ID:(1564, 0)


Gaußsches Gesetz für eine Oberfläche (1)
Gleichung

>Top, >Modell


Mit dem Gaußschen Gesetz

$\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$



für den Fall, dass das Feld auf nur einer Oberfläche normal und konstant ist, haben wir

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$

ID:(11456, 0)


Gaußsches Gesetz für zwei Oberfläche (2)
Gleichung

>Top, >Modell


Mit dem Gaußschen Gesetz

$\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$



für den Fall, dass das Feld auf zwei Oberflächen normal und konstant, haben wir

$ E_1 S_1 + E_2 S_2 = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$

ID:(11458, 0)


Gaußsches Gesetz für drei Flächen (3)
Gleichung

>Top, >Modell


Mit dem Gaußschen Gesetz

$\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$



für den Fall, dass das Feld auf drei Oberflächen normal und konstant ist, haben wir

$ E_1 S_1 + E_2 S_2 + E_3 S_3 = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$

ID:(11457, 0)


Leiterkugel mit Ladung
Bild

>Top


In einer leitenden Kugel mit Ladungen sind diese auf der Oberfläche verteilt und damit ist das Feld im Inneren null. Draußen verhält es sich wie eine Punktladung, die sich in der Mitte der Kugel befindet:

ID:(11451, 0)


Oberfläche einer Kugel
Gleichung

>Top, >Modell


La superficie de una esfera es con igual a

$ S = 4 \pi r ^2$

ID:(4731, 0)


Eine Einzelpunktladung
Gleichung

>Top, >Modell


Im Fall einer sphärischen Gaußschen Oberfläche ist das Feld konstant, so dass es berechnet werden kann durch

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



mit der Oberfläche einer Kugel

$ S = 4 \pi r ^2$



In einem Abstand r einer Last Q ist gleich:

$ E_p =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}$

ID:(11442, 0)


Kugel mit Ladung
Gleichung

>Top, >Modell


Para el caso de una superficie gausseana esférica el campo es constante por lo que se puede calcular con constante de campo eléctrico $C^2/m^2N$, constante dieléctrica $-$, elektrisches Feld $V/m$, ladung $C$ und oberfläche $m^2$ mediante

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



con la superficie de una esfera con pi $rad$, radius eines Kreises $m$ und superficie $m^2$

$ S = 4 \pi r ^2$



A una distancia r de una esfera de carga Q de radio R es igual con pi $rad$, radius eines Kreises $m$ und superficie $m^2$ a:

$ E_f =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}\theta( r - R )$

ID:(11443, 0)


Geladener unendlicher Draht oder Zylinder im Vakuum
Bild

>Top


In einem Leiterdraht oder Zylinder mit Ladungen sind diese über das Objekt verteilt und verhalten sich wie eine lange Kette von Punktlasten, die auf der Achse ausgerichtet sind:

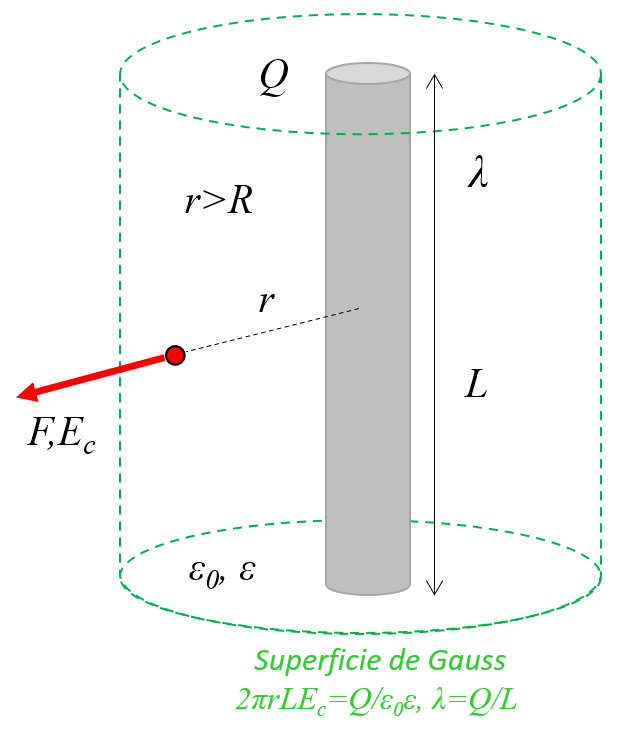
ID:(11452, 0)


Oberfläche eines Zylinders
Hypothese

>Top


Die Oberfläche eines Zylinders mit dem Radius r und der Höhe h wird berechnet nach:

ID:(10464, 0)


Lineare Ladungsdichte
Gleichung

>Top, >Modell


La densidad lineal de carga se calcula como la carga dividida por la carga que contiene el conductor lineal con es:

$ \lambda = \displaystyle\frac{ Q }{ L }$

ID:(11459, 0)


Unendlicher Draht
Gleichung

>Top, >Modell


Im Fall einer zylindrische Gaußschen Oberfläche ist das Feld konstant, so dass es berechnet werden kann durch

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



mit der Oberfläche eines Zylinders

$ $



und die lineare Dichte



In einem Abstand r einer Last pro Länge \lambda ist gleich:

$ E_w =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }$

ID:(11444, 0)


Unendlicher leitender Zylinder
Gleichung

>Top, >Modell


Para el caso de una superficie gausseana cilíndrica el campo es constante por lo que se puede calcular con constante de campo eléctrico $C^2/m^2N$, constante dieléctrica $-$, elektrisches Feld $V/m$, ladung $C$ und oberfläche $m^2$ mediante

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



con la superficie de un cilindro con

$ S =2 \pi r h $



y la densidad lineal con ladung $C$, leitungslänge $m$ und lineare Ladungsdichte $C/m$

$ \lambda = \displaystyle\frac{ Q }{ L }$



A una distancia r de un cilindro infinito de radio R con carga por largo \lambda es con ladung $C$, leitungslänge $m$ und lineare Ladungsdichte $C/m$ igual a:

$ E_c =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }\theta( r - R )$

ID:(11445, 0)


Isolierkugel mit homogener Ladung
Bild

>Top


Eine isolierende Kugel, in der Ladungen homogen verteilt wurden und die nicht bewegt werden kann, weil es sich um ein isolierendes Material handelt, hat ein elektrisches Feld, das im Inneren linear wächst und mit der Umkehrung des quadratischen Radius abnimmt:

ID:(11450, 0)


Isolierkugel mit voller Volumenladung, außen
Gleichung

>Top, >Modell


Para el caso de una superficie gausseana esférica el campo es constante por lo que se puede calcular con constante de campo eléctrico $C^2/m^2N$, constante dieléctrica $-$, elektrisches Feld $V/m$, ladung $C$ und oberfläche $m^2$ mediante

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



con la superficie de una esfera con pi $rad$, radius eines Kreises $m$ und superficie $m^2$

$ S = 4 \pi r ^2$



A una distancia r de una esfera aislante con carga Q en todo el volumen de radio R es con pi $rad$, radius eines Kreises $m$ und superficie $m^2$ igual a:

$ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$

ID:(11446, 0)


Ladungsanteil
Gleichung

>Top, >Modell


Im Fall einer Kugel mit dem Radius R mit homogener Ladung enthält die Gauß-Oberfläche für einen kleineren Radius r eine Ladung gleich

$ q =\displaystyle\frac{ r_i ^3 }{ R ^3 } Q $

ID:(11461, 0)


Isolierkugel mit voller Volumenladung, innen
Gleichung

>Top, >Modell


Para el caso de una superficie gausseana esférica el campo es constante por lo que se puede calcular con constante de campo eléctrico $C^2/m^2N$, constante dieléctrica $-$, elektrisches Feld $V/m$, ladung $C$ und oberfläche $m^2$ mediante

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



con la superficie de una esfera con pi $rad$, radius eines Kreises $m$ und superficie $m^2$

$ S = 4 \pi r ^2$



y la carga encerrada en la superficie gaussiana con eingekapselte Ladung auf der Gauß-Oberfläche $C$, inneres Radius $m$, kugelradius $m$ und ladung $C$

$ q =\displaystyle\frac{ r_i ^3 }{ R ^3 } Q $



A una distancia r del centro de una esfera aislante con carga Q en todo el volumen de radio R es igual con eingekapselte Ladung auf der Gauß-Oberfläche $C$, inneres Radius $m$, kugelradius $m$ und ladung $C$ a:

$ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_i }{ R ^3 }$

ID:(11447, 0)


Unendliche Leiterebene mit Last
Bild

>Top


In einer leitenden Ebene kann eine Gaußsche Oberfläche als Zylinder definiert werden. Die Seitenwände sind orthogonal zum Feld, so dass der einzige Teil, der dazu beiträgt, die Oberflächen parallel zur Ebene sind:

ID:(11453, 0)


Oberflächenladungsdichte
Gleichung

>Top, >Modell


La densidad superficial de carga se calcula como la carga dividida por la superficie con es:

$ \sigma = \displaystyle\frac{ Q }{ S }$

ID:(11460, 0)


Unendliche Platte
Gleichung

>Top, >Modell


Im Fall einer flachen Gaußschen Oberfläche ist das Feld konstant, so dass es berechnet werden kann durch

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



mit der Oberflächendichte der Ladungen

$ \sigma = \displaystyle\frac{ Q }{ S }$



Das Feld für eine unendliche Platte mit einer Ladungsdichte pro Fläche \sigma für den Vakuumfall (\epsilon = 1) ist:

$ E_s =\displaystyle\frac{ \sigma }{ 2 \epsilon_0 \epsilon }$

ID:(11448, 0)


Zwei Platten mit entgegengesetzten Ladungen
Bild

>Top


Bei zwei Platten mit entgegengesetzten Ladungen besteht zwischen ihnen ein Feld größerer Intensität. Es gibt jedoch ein kleines Feld, das mit Feldlinien beschrieben werden kann, die aus einer der Platten austreten und durch eine äußere Drehung der gegenüberliegenden Platte zurückkehren:

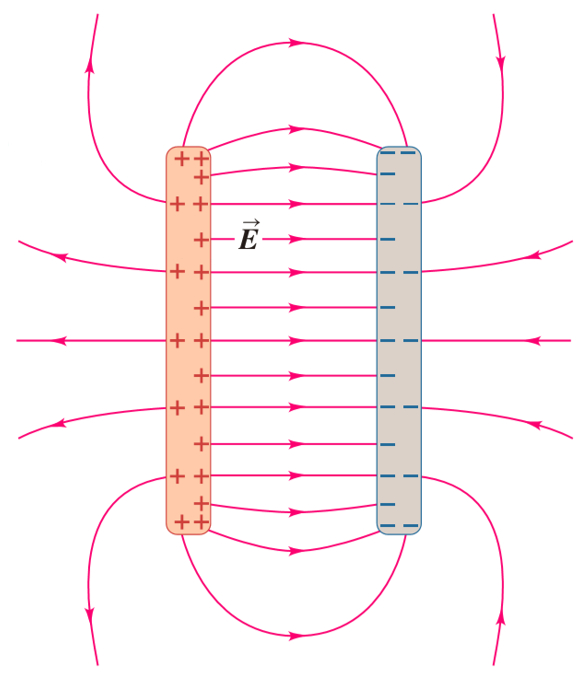
ID:(11454, 0)


Einfaches Modell für zwei Platten mit entgegengesetzten Ladungen
Bild

>Top


Um das Feld zwischen den beiden Platten auf einfache Weise berechnen zu können, kann davon ausgegangen werden, dass das externe Feld kompensiert wird und dass sich das meiste nur zwischen den Platten befindet:

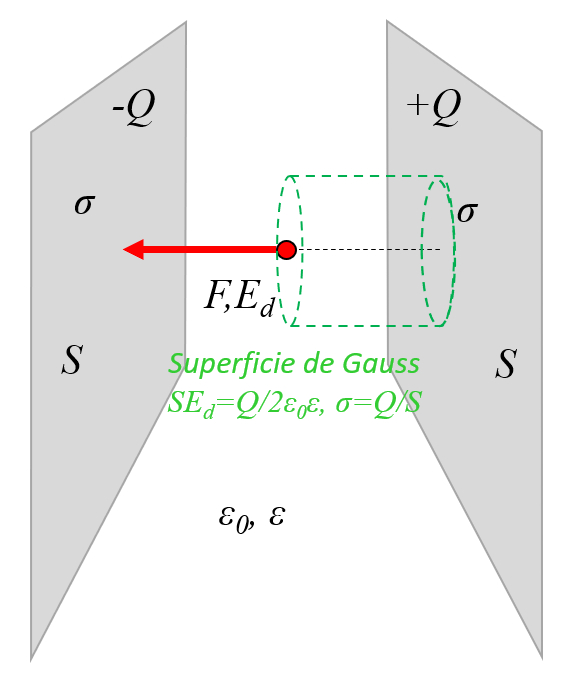
ID:(11455, 0)


Zwei Unendlichkeitsplatten mit gegenüberliegenden Platten
Gleichung

>Top, >Modell


Para el caso de una superficie gausseana plana el campo es constante por lo que se puede con constante de campo eléctrico $C^2/m^2N$, constante dieléctrica $-$, elektrisches Feld $V/m$, ladung $C$ und oberfläche $m^2$ se calcular mediante

$ E S = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$



con la densidad de superficie de cargas con ladung $C$, ladungsdichte nach Fläche $C/m^2$ und oberfläche der Leiters $m^2$

$ \sigma = \displaystyle\frac{ Q }{ S }$



El campo para de dos placa infinita con cargas opuestas con una densidad de carga por área \sigma para el caso del vacío (\epsilon = 1) es con ladung $C$, ladungsdichte nach Fläche $C/m^2$ und oberfläche der Leiters $m^2$:

$ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$

ID:(11449, 0)


0
Video

Video: Beispiele für elektrische Felder