Efecto Stall
Storyboard 
Si el angulo de ataque es muy grande los torbellinos que se forman en la parte superior trasera del ala tienden a avanzar hasta que alcanzan el borde superior al inicio del ala cubriendo toda la parte superior con torbellinos. En esta condición la sustentación desciende dramáticamente generando lo que se denomina el efecto Stall y que puede llevar a una caída descontrolada del objeto (avión/ave).
Existen situaciones en que tanto aviones como aves han usado este efecto para realizar ataques sorpresa desde gran altura desarrollando una técnica para volver a controlar el vuelo y no estrellare en tierra.
ID:(1462, 0)
Efecto Stall
Storyboard 
Si el angulo de ataque es muy grande los torbellinos que se forman en la parte superior trasera del ala tienden a avanzar hasta que alcanzan el borde superior al inicio del ala cubriendo toda la parte superior con torbellinos. En esta condición la sustentación desciende dramáticamente generando lo que se denomina el efecto Stall y que puede llevar a una caída descontrolada del objeto (avión/ave). Existen situaciones en que tanto aviones como aves han usado este efecto para realizar ataques sorpresa desde gran altura desarrollando una técnica para volver a controlar el vuelo y no estrellare en tierra.
Variables
Cálculos
Cálculos
Ecuaciones
La fuerza de sustentación ($F_L$), junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$), se encuentra en
Si consideramos la superficie que genera sustentación ($S_w$), definido por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$),
y para el coeficiente de sustentación ($C_L$), definido como
obtenemos
La fuerza de sustentación ($F_L$) junto con la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) se representa como
lo cual, junto con la masa del cuerpo ($m$) y la aceleración gravitacional ($g$), debe ser igual a:
es decir:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
lo que resulta en:
El coeficiente de sustentación ($C_L$) se calcula con la masa del cuerpo ($m$), la aceleración gravitacional ($g$), la superficie que genera sustentación ($S_w$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) de la siguiente manera:
As , con la constante de proporcionalidad del coeficiente de sustentación ($c$) y el angulo de ataque del ala ($\alpha$)
se obtiene
Ejemplos
El coeficiente de sustentación ($C_L$) es una funci n del ERROR:6121,0 y generalmente sigue la tendencia indicada en la siguiente figura:
En el caso representado, la pendiente es del orden de 1.5 por cada 15 grados, es decir, 0.1 1/grado o 5.73 1/radian.
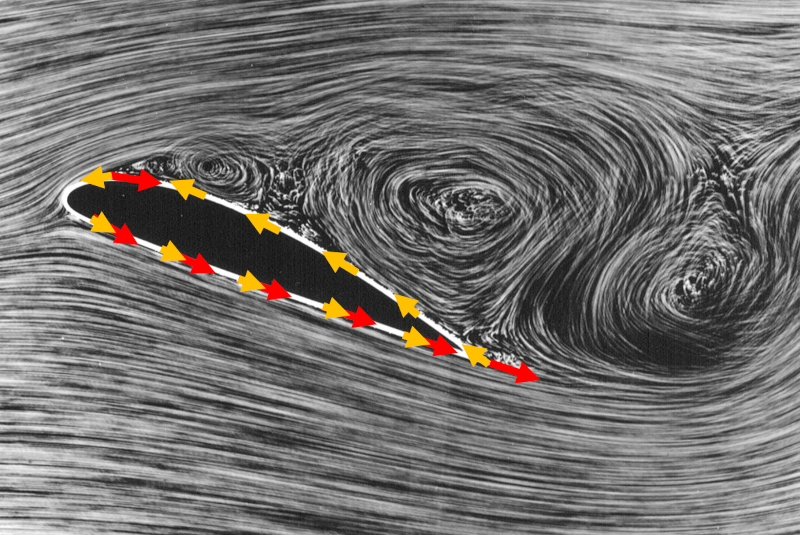
En una maqueta de ala en un t nel de viento, se puede observar c mo al principio el flujo es laminar y, a medida que avanza hacia el extremo del ala, se desarrolla un flujo turbulento:
Cuando el ngulo de ataque supera un valor cr tico (generalmente entre 15 y 30 grados, dependiendo del dise o), la superficie del ala se cubre de v rtices y la sustentaci n disminuye abruptamente hasta llegar a cero.
En este punto, se produce un fen meno conocido como entrada en p rdida (stall), donde el flujo de aire sobre el ala se separa y se forman v rtices turbulentos. Estos v rtices interrumpen el flujo suave del aire, reduciendo dr sticamente la sustentaci n y afectando la capacidad de control de la aeronave. Es fundamental evitar que el ngulo de ataque supere este valor cr tico para mantener la aeronave en vuelo estable y seguro.
A baja velocidad en que el flujo es predominantemente laminar se puede definir y calcular la circulación aerodinamica ($\Gamma$) en torno del objeto.
la circulación aerodinamica ($\Gamma$) permite calcular con el teorema de KuttaJoukowski la fuerza de sustentación ($F_L$) que es con la densidad ($\rho$) y la velocidad respecto del medio ($v$) igual a
El ala genera torbellinos pero estos se arrastran detras del ala sin afectar la circulaci n. Cuando aumenta el angulo de ataque del ala ($\alpha$) los torbellinos comienzan a literalmente subir sobre el ala distorcionando el flujo y con ello la la circulación aerodinamica ($\Gamma$).
En forma simplificada se puede considerar que el tramo con torbellinos no contribueye a la circulaci n reduciendose dramaticamente la fuerza de sustentación ($F_L$) o en su efecto el coeficiente de sustentación ($C_L$).
El vuelo de National Airlines 102, un carguero del tipo Boeing 747-400 que despegaba de Bagram en Afganist n, sufri un tr gico accidente el 29 de abril de 2013 debido al desplazamiento de la carga durante el despegue. Este desplazamiento de la carga provoc un aumento en el ngulo de ataque que llev al ala a perder su capacidad de generar sustentaci n, lo que se conoce como el efecto de entrada en p rdida (stall). Adem s, el desplazamiento de la carga caus da os al sistema hidr ulico de los timones de cola, dejando la aeronave completamente fuera de control. Tr gicamente, los 7 miembros de la tripulaci n perdieron la vida instant neamente en el impacto.
Aqu tienes una simulaci n que muestra el fat dico despegue: Simulaci n
Para crear una presi n mayor debajo que encima del ala y generar sustentaci n, se emplea la Ley de Bernoulli, corrigiendo la falta de conservaci n de la densidad de energ a mediante un coeficiente de sustentación ($C_L$). La presi n sobre el ala, la fuerza de sustentación ($F_L$), se puede estimar utilizando la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) mediante la siguiente f rmula:
A partir de mediciones, se concluye que el coeficiente de sustentación ($C_L$) es proporcional al ERROR:6121,0 siendo la constante de proporcionalidad del coeficiente de sustentación ($c$):
Despu s de cierto ngulo, la curva disminuye hasta llegar a cero. Esto se debe a que sobre dicho ngulo cr tico, los v rtices cubren completamente la superficie superior del ala, lo que resulta en la p rdida de sustentaci n. Este fen meno se conoce como "stall" (entrada en p rdida).
La condici n para lograr el vuelo se cumple cuando la fuerza de sustentación ($F_L$) es igual al peso de la aeronave o ave, calculado a partir de la masa del cuerpo ($m$) y la aceleración gravitacional ($g$). Esto se consigue con suficientes valores adecuados de ERROR:6110,0, la superficie que genera sustentación ($S_w$) y el coeficiente de sustentación ($C_L$), donde este ltimo coeficiente es el factor que se puede ajustar. En el caso de las aeronaves, el piloto puede modificar el valor de el coeficiente de sustentación ($C_L$) utilizando los llamados flaps, cuyo valor debe cumplir con:
Los flaps se ajustan al variar el ngulo que el ala forma con la direcci n de vuelo, conocido como ngulo de ataque.
Como el coeficiente de sustentación ($C_L$) es proprocional al el angulo de ataque del ala ($\alpha$), donde el factor de proprocionalidad es la constante de proporcionalidad del coeficiente de sustentación ($c$) se puede calcular el angulo necesario para volar con la masa del cuerpo ($m$), la aceleración gravitacional ($g$), la superficie que genera sustentación ($S_w$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) mediante:
Es importante considerar que la lienalidad esta limitada a un angulo menor que unos 35 a 40 sobre el cual colapsa en forma catastrofica la sustentaci n. Por ello el angulo de ataque nunca se elige mayor a 30 o en la gerga de la aviaci n flap 30.
ID:(1462, 0)