Usuario:
Introducción a la Geometría
Storyboard 
Muchas de las situaciones se dejan representar geometricamente por lo que es importante conocer los principales elementos y las relaciones que existen entre estos.
ID:(419, 0)
Geometría Básica
Definición
Mediante la geomertia podremos describir la ubicación de objetos en el espacio, de líneas, angulos y figuras geometricas como circulos y tríangulos.
ID:(494, 0)
Puntos y sus Coordenadas
Nota
Cada punto se representa por coordenadas que son las distancias o ángulos por eje para definir la posición:
ID:(1821, 0)
Linea que cruza lineas Paralelas
Script
En el caso de una linea que cruza dos líneas paralelas los ángulos correspondientes son iguales:
ID:(1839, 0)
Triángulos relacionados
Audio
Triángulos en que los lados son paralelos se dicen semejantes:
ID:(1819, 0)
Cuerda
Flujo
Un segmento entre dos dos puntos en la circunferencia de un circulo forma una cuerda:
ID:(1837, 0)
Tangente a un Circulo
Matriz
Una tangente es una recta que tiene solo un punto en común con un circulo.
La tangente es ortogonal al radio el circulo.
ID:(1835, 0)
Introducción a la Geometría
Descripción
Muchas de las situaciones se dejan representar geometricamente por lo que es importante conocer los principales elementos y las relaciones que existen entre estos.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 3323)
(ID 3324)
Ejemplos
Mediante la geomertia podremos describir la ubicaci n de objetos en el espacio, de l neas, angulos y figuras geometricas como circulos y tr angulos.
(ID 494)
Angulo
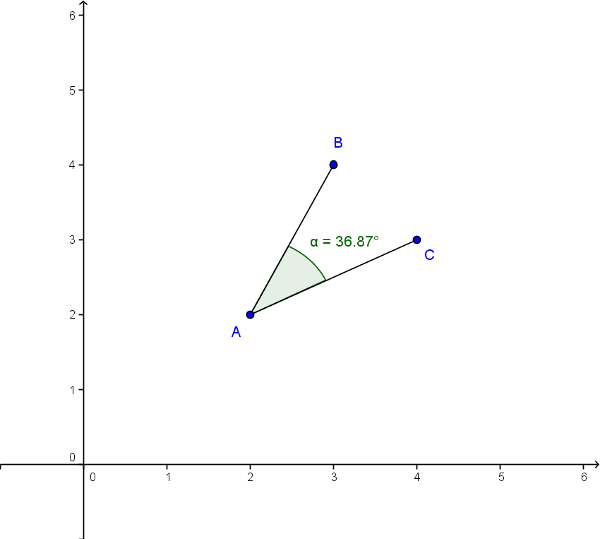
(ID 1834)
Como el per metro de un c rculo es $2\pi r$, ERROR:6294 a lo largo del c rculo corresponder al arco recorrido en el angulo que soporta el Arco ($\theta$), por lo que:
| $ s = r \theta $ |
(ID 3324)
Cada punto se representa por coordenadas que son las distancias o ngulos por eje para definir la posici n:
(ID 1821)
El segmento es una recta finita:
(ID 1822)
La recta es una linea infinita:
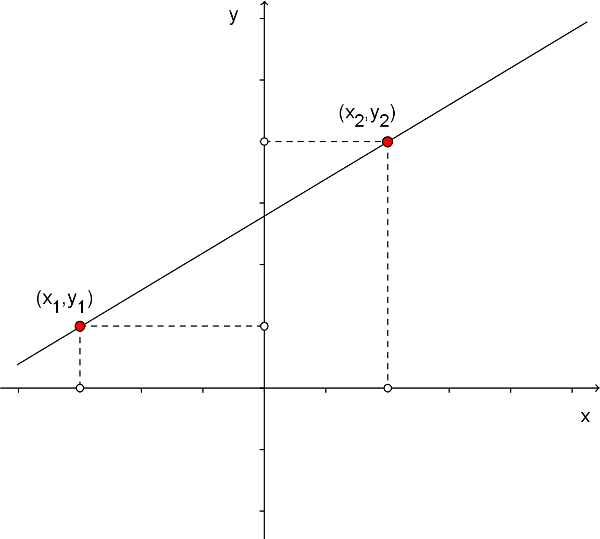
(ID 1832)
En un plano la recta se puede describir por la relaci n
| $ y = m x + b $ |
en donde
(ID 3323)
En un plano la recta se puede describir por la relaci n
| $y = y_0 + m(x - x_0)$ |
en donde
(ID 10838)
L neas paralelas son dos rectas que no se intersectan:
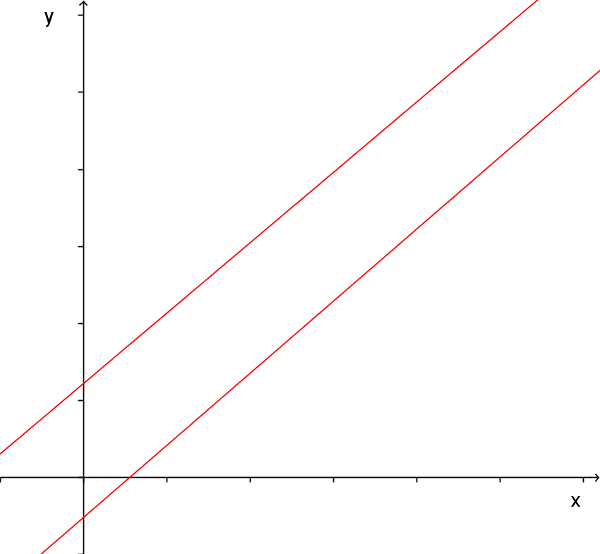
(ID 1838)
En el caso de una linea que cruza dos l neas paralelas los ngulos correspondientes son iguales:
(ID 1839)
Tres lineas que no son paralelas entre ellas forman un triangulo:
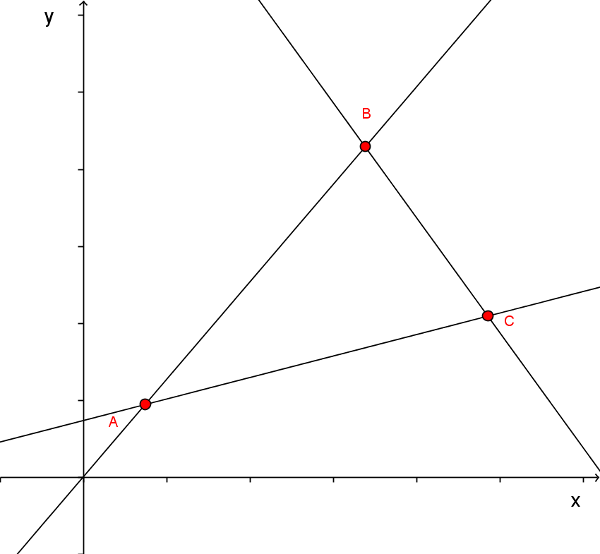
(ID 1820)
Si los ngulos son
| $ \alpha + \beta + \gamma = \pi $ |
(ID 3322)
Dos tri ngulos
| $\displaystyle\frac{\bar{AB}}{\bar{AC}}=\displaystyle\frac{\bar{DE}}{\bar{DF}}$ |
(ID 3263)
Tri ngulos en que los lados son paralelos se dicen semejantes:
(ID 1819)
Relaci n de semejanza de tri ngulos
(ID 1823)
El circulo esta definido por su centro y radio:
(ID 1833)
Si el centro del circulo tiene las coordenadas
| $( x - x_0 )^2+( y - y_0 )^2= r ^2$ |
La ecuaci n corresponde a la ecuaci n de un circulo.
(ID 3325)
Una recta que intersecta un circulo forma una secante:
(ID 1836)
Un segmento entre dos dos puntos en la circunferencia de un circulo forma una cuerda:
(ID 1837)
Una tangente es una recta que tiene solo un punto en com n con un circulo.
La tangente es ortogonal al radio el circulo.
(ID 1835)
ID:(419, 0)