Interceptar em velocidade angular constante
Storyboard 
Os objetos podem se interceptar quando coincidem em ângulo em um mesmo momento. Para alcançar isso, eles devem se deslocar a partir de seus respectivos ângulos iniciais com velocidades angulares que lhes permitam coincidir em ângulo e tempo no final da viagem.
ID:(1450, 0)
Conceito de interceptação
Imagem 
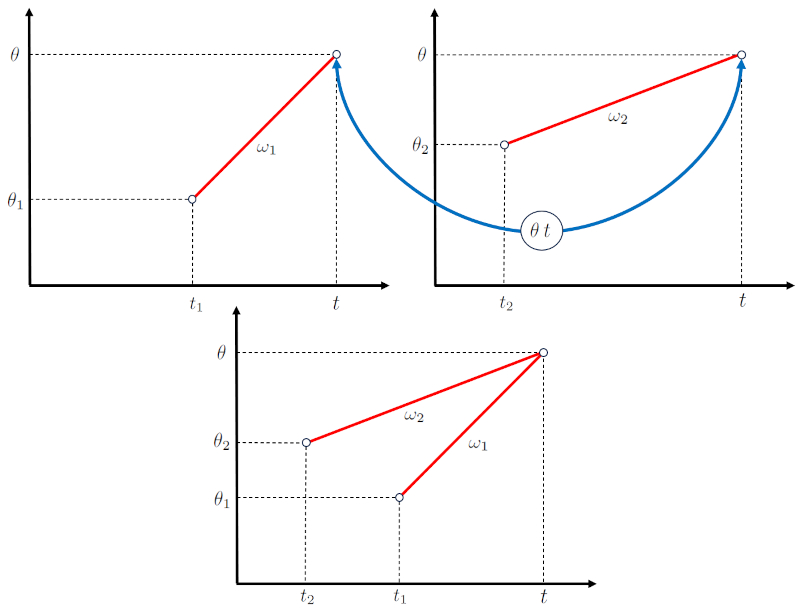
No caso de uma interseção, trata-se de dois corpos que se movem de tal forma que se encontrarão em ERROR:10307,0 no tempo um tempo de interseção ($t$).
Para alcançar isso, cada corpo:
• Começa seu deslocamento em o tempo inicial do primeiro objeto ($t_1$) em o ângulo inicial do primeiro corpo ($\theta_1$) com uma velocidade angular do corpo 1 ($\omega_1$).
• Começa seu deslocamento em o tempo inicial do segundo objeto ($t_2$) em o ângulo inicial do segundo corpo ($\theta_2$) com uma velocidade angular do corpo 2 ($\omega_2$).
Essas condições devem ser cumpridas para alcançar a interseção.
Com isso, os diagramas de ângulo-tempo podem ser sobrepostos como mostrado na seguinte representação:
ID:(15517, 0)
Ângulos e durações de viagem
Nota 
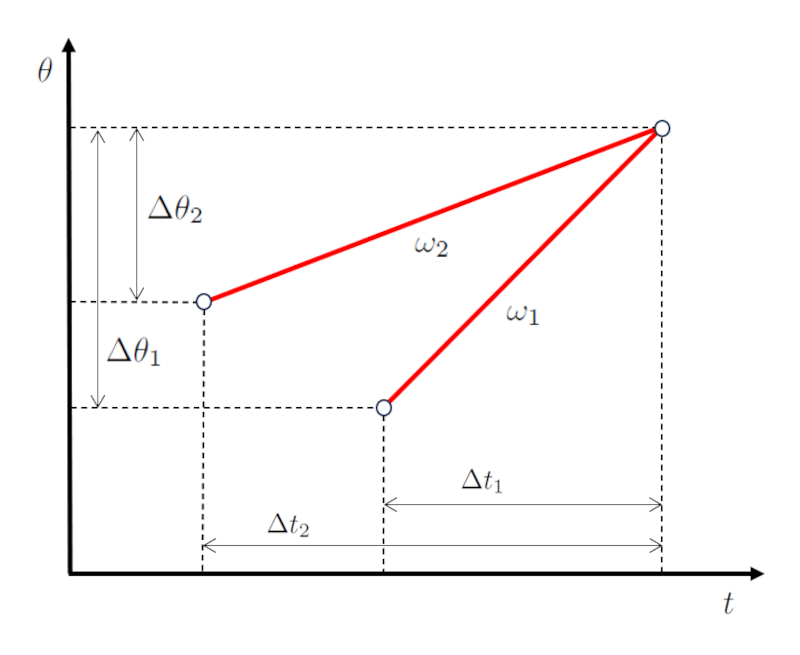
No caso de uma interseção ou colisão entre dois objetos, é comum que la velocidade angular do corpo 1 ($\omega_1$) e la velocidade angular do corpo 2 ($\omega_2$) precisem ser configurados de forma que coincidam.
Isso significa que o ângulo percorrido pelo primeiro corpo ($\Delta\theta_1$) e la tempo de percurso do primeiro objeto ($\Delta t_1$) devem resultar em uma velocidade angular do corpo 1 ($\omega_1$),
| $ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$ |
de modo que com o ângulo percorrido pelo segundo corpo ($\Delta\theta_2$) e la tempo de percurso do segundo objeto ($\Delta t_2$) obtemos uma velocidade angular do corpo 2 ($\omega_2$),
| $ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$ |
para que finalmente coincidam em tempo e espaço (posição):
ID:(15516, 0)
Ângulo e tempo de interceptação
Citar 
No caso de um movimento em que dois objetos se interceptam, como la ângulo de intersecção ($\theta$) e o tempo de interseção ($t$), é comum para ambos. Portanto, se para o primeiro objeto o tempo inicial do primeiro objeto ($t_1$) e o ângulo inicial do primeiro corpo ($\theta_1$) com la velocidade angular do corpo 1 ($\omega_1$) forem atendidos:
| $ \theta = \theta_1 + \omega_1 ( t - t_1 )$ |
e para o segundo objeto o tempo inicial do segundo objeto ($t_2$) e o ângulo inicial do segundo corpo ($\theta_2$) com la velocidade angular do corpo 2 ($\omega_2$) forem atendidos:
| $ \theta = \theta_2 + \omega_2 ( t - t_2 )$ |
que é representado como:

ID:(15518, 0)
Interceptar em velocidade angular constante
Descrição 
Os objetos podem se interceptar quando coincidem em ângulo em um mesmo momento. Para alcançar isso, eles devem se deslocar a partir de seus respectivos ângulos iniciais com velocidades angulares que lhes permitam coincidir em ângulo e tempo no final da viagem.
Variáveis
Cálculos
Cálculos
Equações
No caso em que la velocidade angular inicial ($\omega_0$) igual a la velocidade angular média ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Portanto, com la diferença de ângulos ($\Delta\theta$), que igual a o ângulo ($\theta$) dividido por o ângulo inicial ($\theta_0$), obtemos:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
E com o tempo decorrido ($\Delta t$), que igual a o tempo ($t$) dividido por o tempo inicial ($t_0$), obtemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescrever a equa o para la velocidade angular média ($\bar{\omega}$) como:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Isso pode ser expresso como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Ao resolver, obtemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
No caso em que la velocidade angular inicial ($\omega_0$) igual a la velocidade angular média ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Portanto, com la diferença de ângulos ($\Delta\theta$), que igual a o ângulo ($\theta$) dividido por o ângulo inicial ($\theta_0$), obtemos:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
E com o tempo decorrido ($\Delta t$), que igual a o tempo ($t$) dividido por o tempo inicial ($t_0$), obtemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescrever a equa o para la velocidade angular média ($\bar{\omega}$) como:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Isso pode ser expresso como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Ao resolver, obtemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Como la velocidade média ($\bar{v}$) com la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$), igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
e com la distância percorrida em um tempo ($\Delta s$) expresso como arco de um c rculo, e o rádio ($r$) e la variação de ângulo ($\Delta\theta$) s o
| $ \Delta s=r \Delta\theta $ |
e a defini o de la velocidade angular média ($\bar{\omega}$)
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
ent o,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como a rela o geral, pode ser aplicada para valores instant neos, resultando em
| $ v = r \omega $ |
(ID 3233)
Como la velocidade média ($\bar{v}$) com la distância percorrida em um tempo ($\Delta s$) e o tempo decorrido ($\Delta t$), igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
e com la distância percorrida em um tempo ($\Delta s$) expresso como arco de um c rculo, e o rádio ($r$) e la variação de ângulo ($\Delta\theta$) s o
| $ \Delta s=r \Delta\theta $ |
e a defini o de la velocidade angular média ($\bar{\omega}$)
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
ent o,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como a rela o geral, pode ser aplicada para valores instant neos, resultando em
| $ v = r \omega $ |
(ID 3233)
A defini o de la velocidade angular média ($\bar{\omega}$) considerada como la variação de ângulo ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
e o tempo decorrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
A rela o entre ambos definida como la velocidade angular média ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
A defini o de la velocidade angular média ($\bar{\omega}$) considerada como la variação de ângulo ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
e o tempo decorrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
A rela o entre ambos definida como la velocidade angular média ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Exemplos
(ID 15411)
No caso de uma interse o, trata-se de dois corpos que se movem de tal forma que se encontrar o em ERROR:10307,0 no tempo um tempo de interseção ($t$).
Para alcan ar isso, cada corpo:
• Come a seu deslocamento em o tempo inicial do primeiro objeto ($t_1$) em o ângulo inicial do primeiro corpo ($\theta_1$) com uma velocidade angular do corpo 1 ($\omega_1$).
• Come a seu deslocamento em o tempo inicial do segundo objeto ($t_2$) em o ângulo inicial do segundo corpo ($\theta_2$) com uma velocidade angular do corpo 2 ($\omega_2$).
Essas condi es devem ser cumpridas para alcan ar a interse o.
Com isso, os diagramas de ngulo-tempo podem ser sobrepostos como mostrado na seguinte representa o:

(ID 15517)
No caso de uma interse o ou colis o entre dois objetos, comum que la velocidade angular do corpo 1 ($\omega_1$) e la velocidade angular do corpo 2 ($\omega_2$) precisem ser configurados de forma que coincidam.
Isso significa que o ângulo percorrido pelo primeiro corpo ($\Delta\theta_1$) e la tempo de percurso do primeiro objeto ($\Delta t_1$) devem resultar em uma velocidade angular do corpo 1 ($\omega_1$),
| $ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$ |
de modo que com o ângulo percorrido pelo segundo corpo ($\Delta\theta_2$) e la tempo de percurso do segundo objeto ($\Delta t_2$) obtemos uma velocidade angular do corpo 2 ($\omega_2$),
| $ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$ |
para que finalmente coincidam em tempo e espa o (posi o):

(ID 15516)
No caso de um movimento em que dois objetos se interceptam, como la ângulo de intersecção ($\theta$) e o tempo de interseção ($t$), comum para ambos. Portanto, se para o primeiro objeto o tempo inicial do primeiro objeto ($t_1$) e o ângulo inicial do primeiro corpo ($\theta_1$) com la velocidade angular do corpo 1 ($\omega_1$) forem atendidos:
| $ \theta = \theta_1 + \omega_1 ( t - t_1 )$ |
e para o segundo objeto o tempo inicial do segundo objeto ($t_2$) e o ângulo inicial do segundo corpo ($\theta_2$) com la velocidade angular do corpo 2 ($\omega_2$) forem atendidos:
| $ \theta = \theta_2 + \omega_2 ( t - t_2 )$ |
que representado como:

(ID 15518)
(ID 15422)
Para descrever a rota o de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso feito subtraindo o ângulo inicial ($\theta_0$) do valor alcan ado pelo objeto durante sua rota o, que o ângulo ($\theta$):
| $ \Delta\theta = \theta_2 - \theta_1 $ |
(ID 3680)
Para descrever a rota o de um objeto, precisamos determinar la variação de ângulo ($\Delta\theta$). Isso feito subtraindo o ângulo inicial ($\theta_0$) do valor alcan ado pelo objeto durante sua rota o, que o ângulo ($\theta$):
| $ \Delta\theta = \theta_2 - \theta_1 $ |
(ID 3680)
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
| $ \Delta t \equiv t - t_0 $ |
(ID 4353)
Para descrever o movimento de um objeto, precisamos calcular o tempo decorrido ($\Delta t$). Essa magnitude obtida medindo o tempo inicial ($t_0$) e o o tempo ($t$) desse movimento. A dura o determinada subtraindo o tempo inicial do tempo final:
| $ \Delta t \equiv t - t_0 $ |
(ID 4353)
No caso em que a velocidade angular constante, la velocidade angular média ($\bar{\omega}$) coincide com o valor de la velocidade angular inicial ($\omega_0$), ent o
| $ \bar{\omega} = \omega_0 $ |
Nesse cen rio, podemos calcular o ngulo percorrido em fun o do tempo lembrando que ele est associado diferen a entre os ngulos atual e inicial, bem como o tempo atual e o inicial. Portanto, o ângulo ($\theta$) igual a o ângulo inicial ($\theta_0$), la velocidade angular inicial ($\omega_0$), o tempo ($t$) e o tempo inicial ($t_0$) conforme mostrado abaixo:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
A equa o representa uma reta no espa o ngulo-tempo.
(ID 1023)
No caso em que a velocidade angular constante, la velocidade angular média ($\bar{\omega}$) coincide com o valor de la velocidade angular inicial ($\omega_0$), ent o
| $ \bar{\omega} = \omega_0 $ |
Nesse cen rio, podemos calcular o ngulo percorrido em fun o do tempo lembrando que ele est associado diferen a entre os ngulos atual e inicial, bem como o tempo atual e o inicial. Portanto, o ângulo ($\theta$) igual a o ângulo inicial ($\theta_0$), la velocidade angular inicial ($\omega_0$), o tempo ($t$) e o tempo inicial ($t_0$) conforme mostrado abaixo:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
A equa o representa uma reta no espa o ngulo-tempo.
(ID 1023)
Para estimar o deslocamento de um objeto, necess rio conhecer sua la velocidade angular ($\omega$) em fun o de o tempo ($t$). Portanto, introduz-se a la velocidade angular média ($\bar{\omega}$), definida como a propor o entre la variação de ângulo ($\Delta\theta$) e o tempo decorrido ($\Delta t$).
Para medir isso, pode-se utilizar um sistema como o mostrado na imagem:

Para determinar a velocidade angular m dia, um elemento refletor colocado no eixo ou em um disco com v rios elementos refletores, e o movimento registrado para estimar o comprimento do arco $\Delta s$ e o ngulo associado ao raio $r$. Em seguida, a diferen a de tempo quando a marca passa diante do sensor registrada como $\Delta t$. A velocidade angular m dia determinada dividindo-se o ngulo percorrido pelo tempo decorrido.
A equa o que descreve a velocidade angular m dia :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Deve-se notar que a velocidade m dia uma estimativa da velocidade angular real. O principal problema que:
Se a velocidade angular varia durante o tempo decorrido, o valor da velocidade angular m dia pode ser muito diferente da velocidade angular m dia.
Portanto, a chave :
Determinar a velocidade em um tempo decorrido suficientemente curto para minimizar sua varia o.
(ID 3679)
Para estimar o deslocamento de um objeto, necess rio conhecer sua la velocidade angular ($\omega$) em fun o de o tempo ($t$). Portanto, introduz-se a la velocidade angular média ($\bar{\omega}$), definida como a propor o entre la variação de ângulo ($\Delta\theta$) e o tempo decorrido ($\Delta t$).
Para medir isso, pode-se utilizar um sistema como o mostrado na imagem:

Para determinar a velocidade angular m dia, um elemento refletor colocado no eixo ou em um disco com v rios elementos refletores, e o movimento registrado para estimar o comprimento do arco $\Delta s$ e o ngulo associado ao raio $r$. Em seguida, a diferen a de tempo quando a marca passa diante do sensor registrada como $\Delta t$. A velocidade angular m dia determinada dividindo-se o ngulo percorrido pelo tempo decorrido.
A equa o que descreve a velocidade angular m dia :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Deve-se notar que a velocidade m dia uma estimativa da velocidade angular real. O principal problema que:
Se a velocidade angular varia durante o tempo decorrido, o valor da velocidade angular m dia pode ser muito diferente da velocidade angular m dia.
Portanto, a chave :
Determinar a velocidade em um tempo decorrido suficientemente curto para minimizar sua varia o.
(ID 3679)
Se dividirmos a rela o entre la distância percorrida em um tempo ($\Delta s$) e o rádio ($r$) por la variação de ângulo ($\Delta\theta$),
| $ \Delta s=r \Delta\theta $ |
e ent o dividirmos isso por o tempo decorrido ($\Delta t$), obtemos a rela o que nos permite calcular la velocidade ($v$) ao longo da rbita, conhecida como velocidade tangencial, que est associada a la velocidade angular ($\omega$):
| $ v = r \omega $ |
(ID 3233)
Se dividirmos a rela o entre la distância percorrida em um tempo ($\Delta s$) e o rádio ($r$) por la variação de ângulo ($\Delta\theta$),
| $ \Delta s=r \Delta\theta $ |
e ent o dividirmos isso por o tempo decorrido ($\Delta t$), obtemos a rela o que nos permite calcular la velocidade ($v$) ao longo da rbita, conhecida como velocidade tangencial, que est associada a la velocidade angular ($\omega$):
| $ v = r \omega $ |
(ID 3233)
ID:(1450, 0)
