Aceleração angular instantânea
Storyboard 
Para descrever como a velocidade angular evolui ao longo do tempo, é necessário estudar a variação desta em relação ao tempo.
A relação da variação da velocidade angular equivale à mudança na velocidade angular ao longo do tempo decorrido, que, quando dividida por esse tempo, corresponde à aceleração angular.
Para um intervalo de tempo infinitesimal, a aceleração angular corresponde à aceleração angular instantânea.
ID:(1452, 0)
Aceleração angular como derivada
Imagem 
Se um intervalo de tempo $t$ é considerado com uma velocidade angular $\omega(t)$ e um ponto é observado em um tempo futuro $t+\Delta t$ com uma velocidade angular $\omega(t+\Delta t)$, a aceleração angular pode ser estimada como a variação
$\omega(t+\Delta t)-\omega(t)$
ao longo do tempo $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
À medida que o valor de $\Delta t$ diminui, a aceleração assume o papel da tangente à curva de velocidade naquele momento:
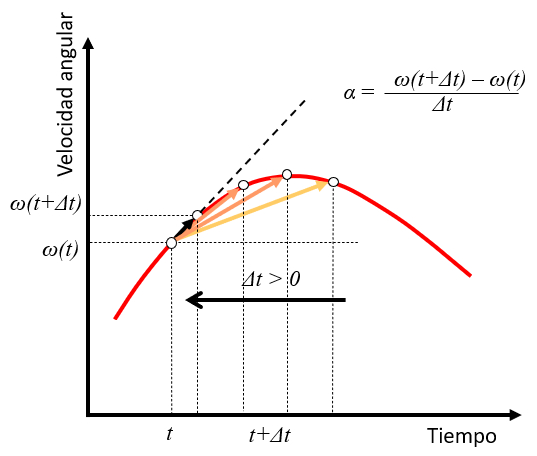
Isso generaliza o que já foi visto para o caso da aceleração angular constante.
ID:(11413, 0)
Velocidade Angular como Integral da Aceleração
Nota 
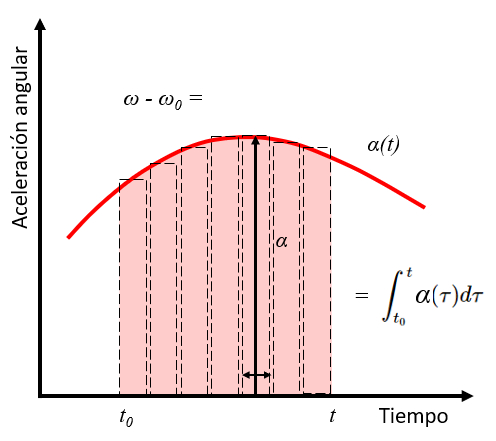
A integral de uma função corresponde à área sob a curva que define essa função. Portanto, a integral da aceleração angular entre os tempos $t_0$ e $t$ corresponde à variação da velocidade angular entre a velocidade angular inicial $\omega_0$ e $\omega$.
Assim, utilizando aceleração angular instantânea $rad/s^2$, tempo $s$, tempo inicial $s$, velocidade angular $rad/s$ e velocidade angular inicial $rad/s$, obtemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Isso é ilustrado no seguinte gráfico:
ID:(11415, 0)
Aceleração tangencial, regra da mão direita
Citar 
A orientação da aceleração tangencial pode ser obtida utilizando a regra da mão direita, onde os dedos apontam em direção ao eixo e depois giram em direção ao raio:

ID:(11600, 0)
Aceleração angular instantânea
Descrição 
Para descrever como a velocidade angular evolui ao longo do tempo, é necessário estudar a variação desta em relação ao tempo. A relação da variação da velocidade angular equivale à mudança na velocidade angular ao longo do tempo decorrido, que, quando dividida por esse tempo, corresponde à aceleração angular. Para um intervalo de tempo infinitesimal, a aceleração angular corresponde à aceleração angular instantânea.
Variáveis
Cálculos
Cálculos
Equações
Dado que a acelera o tangencial
| $ a = r \alpha $ |
Se o vetor unit rio do eixo $\hat{n}$ e o vetor unit rio radial $\hat{r}$, o vetor unit rio tangencial pode ser calculado usando o produto cruz:
$\hat{t} = \hat{n} \times \hat{r}$
Consequentemente, considerando que
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
e
$\vec{\alpha} = \alpha \hat{n}$
,
podemos deduzir que
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
o que se traduz em
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
.
(ID 11598)
Exemplos
(ID 15415)
Se um intervalo de tempo $t$ considerado com uma velocidade angular $\omega(t)$ e um ponto observado em um tempo futuro $t+\Delta t$ com uma velocidade angular $\omega(t+\Delta t)$, a acelera o angular pode ser estimada como a varia o
$\omega(t+\Delta t)-\omega(t)$
ao longo do tempo $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
medida que o valor de $\Delta t$ diminui, a acelera o assume o papel da tangente curva de velocidade naquele momento:

Isso generaliza o que j foi visto para o caso da acelera o angular constante.
(ID 11413)
A integral de uma fun o corresponde rea sob a curva que define essa fun o. Portanto, a integral da acelera o angular entre os tempos $t_0$ e $t$ corresponde varia o da velocidade angular entre a velocidade angular inicial $\omega_0$ e $\omega$.
Assim, utilizando aceleração angular instantânea $rad/s^2$, tempo $s$, tempo inicial $s$, velocidade angular $rad/s$ e velocidade angular inicial $rad/s$, obtemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Isso ilustrado no seguinte gr fico:

(ID 11415)
A orienta o da acelera o tangencial pode ser obtida utilizando a regra da m o direita, onde os dedos apontam em dire o ao eixo e depois giram em dire o ao raio:

(ID 11600)
(ID 15426)
Assim como na acelera o de transla o, existe o conceito de acelera o angular instant nea, que a acelera o angular com
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
que existe em um momento espec fico. Isso calculado na aproxima o de intervalos de tempo muito pequenos $(\Delta t\rightarrow 0)$, ou seja
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
onde
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
(ID 3235)
Se integrarmos a defini o da velocidade angular em rela o ao tempo, utilizando aceleração angular instantânea $rad/s^2$, tempo $s$ e velocidade angular instantânea $rad/s$, obtemos:
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
Isso significa que, para um intervalo de tempo $dt$, o ngulo percorrido dado por:
$d\omega = \alpha dt$
Se considerarmos $N$ intervalos $dt_i$ com velocidades angulares correspondentes $\alpha_i$, o ngulo total percorrido ser :
$\omega - \omega_0 = \sum_i \alpha_i dt_i$
Considerando a curva de velocidade angular-tempo, os elementos $\alpha_i dt_i$ correspondem a ret ngulos com altura $\alpha_i$ e largura $dt_i$. A soma, portanto, corresponde rea sob a curva de velocidade angular-tempo. Assim, a soma pode ser expressa como uma integral utilizando aceleração angular instantânea $rad/s^2$, tempo $s$ e velocidade angular instantânea $rad/s$:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
(ID 11416)
Podemos entender a acelera o de forma geral como uma entidade em tr s dimens es, ou seja, vetorial. Isso significa que sua velocidade precisa ser descrita por um vetor de velocidade angular $\vec{\omega}$, para o qual podemos definir um componente de acelera o com aceleração angular instantânea $rad/s^2$, tempo $s$ e velocidade angular instantânea $rad/s$
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
Com isso, podemos generalizar a acelera o com:
| $ \vec{alpha} =\displaystyle\frac{d \vec{\omega} }{d t }$ |
(ID 6742)
A integra o da defini o diferencial, ou seja, das varia es temporais infinitesimais, com rela o equa o resulta em:
| $ a =\displaystyle\frac{ d v }{ d t }$ |
Podemos realizar a integra o entre o tempo $t_0$ e $t$ da acelera o $a(\tau)$ para obter a velocidade $v(t)$ se a velocidade inicial for $v_0$, utilizando a equa o:
| $ v = v_0 +\displaystyle\int_{t_0}^t a(\tau) d\tau $ |
(ID 11414)
A acelera o angular representada como um vetor na dire o do eixo de rota o. Como o raio de rota o e a acelera o angular s o ortogonais acelera o tangencial, temos:
| $ a = r \alpha $ |
Essa rela o pode ser expressa como o produto cruz entre a acelera o angular e o raio, representado da seguinte forma:
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
(ID 11598)
ID:(1452, 0)
