Flotación
Storyboard 
Cuando un cuerpo está sumergido en un medio líquido, experimenta la presión de este entorno. Dado que la presión aumenta con la profundidad, esta será mayor en la parte inferior del cuerpo que en la superior, lo que genera una fuerza dirigida hacia la superficie, conocida como fuerza de sustentación. Si esta fuerza es mayor que la gravedad del cuerpo, éste se elevará a la superficie y flotará. Si es menor, reducirá la velocidad con la que se hunde, pero seguirá descendiendo hasta tocar fondo.
ID:(1609, 0)
Sustentación
Concepto 
Cuando se sumerge un objeto que cuelga de un dinamómetro en un líquido, se observa que la fuerza indicada por este se reduce, lo que indica la existencia de una fuerza de empuje una fuerza de flotación ($F_b$) generada por el líquido.

Cuando un objeto flota, la fuerza de empuje la fuerza de flotación ($F_b$) tiene que ser igual la fuerza gravitacional ($F_g$), lo que explica que no se hunda ni emerja.
ID:(11951, 0)
Presión en torno de un cuerpo sumergido
Concepto 
Para explicar la sustentación experimentada por un cuerpo sumergido, es necesario estudiar las presiones verticales a las que está expuesto. Dado que la cara inferior del cuerpo se encuentra a una mayor profundidad que la cara superior, la presión en la parte inferior es mayor que en la parte superior, lo que resulta en una fuerza neta hacia arriba que genera la sustentación observada. Este fenómeno es similar cuando un cuerpo flota en la superficie, donde no hay presión del agua sobre él; nuevamente, es la presión en la parte inferior la que genera la sustentación.

Por lo tanto, en el caso en que el cuerpo esté sumergido, se obtiene:
$\Delta p = p_2 - p_1 = \rho_w g h_2-\rho_w g h_1=\rho_w g (h_2 - h_1) = \rho_w g d$
O de manera similar en la superficie:
| $ \Delta p = \rho_w g d $ |
Finalmente, la fuerza de sustentación se obtiene utilizando la definición de presión, que para la presión en la base ($\Delta p$) con la fuerza de flotación ($F_b$) y la sección del cuerpo que flota ($S_s$) corresponde a:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
ID:(11952, 0)
Principio de Arquímedes
Concepto 
Un cuerpo flota si la fuerza de empuje la fuerza de flotación ($F_b$) es igual al peso del cuerpo la fuerza gravitacional ($F_g$):
| $ F_b = F_g $ |
Lo cual implica que la relación entre la masa del objeto que flota ($M_s$) y la masa de líquido desplazado ($M_b$) establece:
| $ M_b = M_s $ |
Lo cual corresponde al principio de Arquímedes [1].

que dice
Todo objeto flotante desplaza su propio peso en liquido.
![]() [1] "Peri ton ochoumenon" (Sobre cuerpos flotantes), Arquímedes, 287 a 212 a.C.
[1] "Peri ton ochoumenon" (Sobre cuerpos flotantes), Arquímedes, 287 a 212 a.C.
ID:(11956, 0)
Volumen de aire bajo el nivel de flotación
Concepto 
Dado que con la masa del objeto que flota ($M_s$) y la masa de líquido desplazado ($M_b$)
| $ M_b = M_s $ |
se relaciona con la densidad del objeto ($\rho_s$) y el volumen del objeto ($V_s$) por
| $ \rho_s \equiv\displaystyle\frac{ M_s }{ V_s }$ |
mientras que se cumple que con la densidad del líquido ($\rho_w$) y el volumen de lastre ($V_w$) tenemos
| $ M_b = \rho_w ( V_s + V_w )$ |
se obtiene la relación
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
De esta manera, un objeto con una densidad mayor que la del agua puede flotar siempre que tenga un volumen de aire por debajo del nivel de flotación (superficie del agua). En el caso de un barco, esto corresponde a los espacios que ocupan la carga y/o los pasajeros, mientras que en un submarino son los tanques de lastre, y en un pez es la vejiga natatoria.
Es importante destacar que:
Para un objeto sumergido, la suspensión, ascenso o descenso no dependen de la profundidad en la que se encuentre. Sin embargo, la capacidad de bombear aire al tanque de lastre o vejiga natatoria sí depende de la presión circundante.
La densidad del agua no es homogénea en el mar, lo que hace que un objeto sumergido tenga que ajustar el volumen utilizado en el tanque de lastre o vejiga natatoria a medida que se desplaza.
ID:(15706, 0)
Métodos de flotación
Concepto 
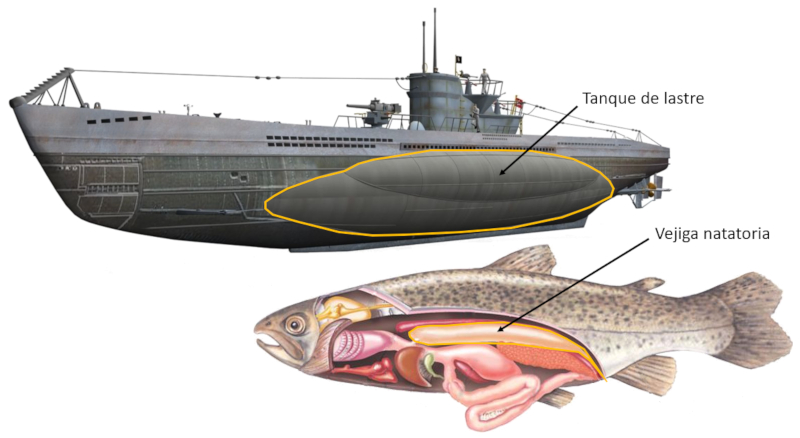
Los submarinos y los peces tienen la capacidad de ajustar la profundidad a la que se mantienen en el agua. Pueden ascender hacia la superficie (flotar) o descender, limitados solo por la presión que pueden soportar. Esto lo logran mediante el uso de lastres (en submarinos) y vejigas natatorias (en peces), que son espacios donde se puede expandir el aire, ocupando así un mayor volumen de agua desplazada.
Para lograr esto, la igualdad entre la masa de líquido desplazado ($M_b$) y la masa del objeto que flota ($M_s$) se puede reescribir en función de la densidad del líquido ($\rho_w$), la densidad del objeto ($\rho_s$) y el volumen del objeto ($V_s$), lo que permite ajustar el volumen de lastre ($V_w$):
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
permitiendo que una de las dos sea igual o supere a la otra. En resumen, si se aumenta el volumen de lastre ($V_w$), se aumenta la sustentación y se asciende; si se reduce el volumen, se hunde. Si se mantiene el volumen igual, se mantienen en suspensión.
Un estudio interesante sobre cómo las ballenas usan el órgano de espermaceti para controlar la flotabilidad mediante calor y grasas se puede leer en el estudio "Control de flotabilidad como función del órgano de espermaceti en el cachalote" de Malcolm R. Clarke, publicado en J.mar.bio.Ass U.K. (1978) 58, 27-71.
ID:(11958, 0)
Flotación
Descripción 
Cuando un cuerpo está sumergido en un medio líquido, experimenta la presión de este entorno. Dado que la presión aumenta con la profundidad, esta será mayor en la parte inferior del cuerpo que en la superior, lo que genera una fuerza dirigida hacia la superficie, conocida como fuerza de sustentación. Si esta fuerza es mayor que la gravedad del cuerpo, éste se elevará a la superficie y flotará. Si es menor, reducirá la velocidad con la que se hunde, pero seguirá descendiendo hasta tocar fondo.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3241)
(ID 3792)
La presi n se define como:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
La diferencia de presi n es:
| $ \Delta p = \rho_w g \Delta h $ |
La secci n por la altura del cuerpo es igual al volumen:
| $ V_b = S_s d $ |
Por lo tanto, la fuerza de sustentaci n de un cuerpo sumergido es:
$F_b = S \Delta p = \rho S \Delta h g = \rho V_s g$
Es decir:
| $ F_b = \rho_w V_b g $ |
(ID 11953)
La fuerza de flotación ($F_b$) est determinada por la densidad del líquido ($\rho_w$), el volumen desplazado ($V_b$) y la aceleración gravitacional ($g$) como:
| $ F_b = \rho_w V_b g $ |
lo cual se opone a la fuerza gravitacional ($F_g$) con la masa del objeto que flota ($M_s$) seg n:
| $ F_g = M_s g $ |
por lo tanto, con la masa de líquido desplazado ($M_b$) y la masa del objeto que flota ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
se tiene que
| $ M_b = M_s $ |
(ID 11955)
Dado que con la masa del objeto que flota ($M_s$) y la masa de líquido desplazado ($M_b$)
| $ M_b = M_s $ |
se relaciona con la densidad del objeto ($\rho_s$) y el volumen del objeto ($V_s$) por
| $ \rho_s \equiv\displaystyle\frac{ M_s }{ V_s }$ |
mientras que se cumple que con la densidad del líquido ($\rho_w$) y el volumen de lastre ($V_w$) tenemos
| $ M_b = \rho_w ( V_s + V_w )$ |
se obtiene la relaci n
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
(ID 11978)
(ID 12015)
Dado que el volumen desplazado ($V_b$) es el volumen sumergido ($V_s$), pero incluyendo el volumen de lastre ($V_w$), se obtiene
| $ V_b = V_s + V_w $ |
y la ecuaci n de la densidad del líquido ($\rho_w$) representada por
| $ \rho_w \equiv\displaystyle\frac{ M_b }{ V_b }$ |
se puede calcular la masa de líquido desplazado ($M_b$) como
| $ M_b = \rho_w ( V_s + V_w )$ |
(ID 12016)
La fuerza de flotación ($F_b$) est determinada por la densidad del líquido ($\rho_w$), el volumen desplazado ($V_b$) y la aceleración gravitacional ($g$) seg n:
| $ F_b = \rho_w V_b g $ |
lo cual se opone a la fuerza gravitacional ($F_g$) con la masa del objeto que flota ($M_s$) seg n:
| $ F_g = M_s g $ |
Si ambas fuerzas son iguales:
| $ F_b = F_g $ |
el objeto flotar .
(ID 13406)
Ejemplos
(ID 15480)
Cuando se sumerge un objeto que cuelga de un dinam metro en un l quido, se observa que la fuerza indicada por este se reduce, lo que indica la existencia de una fuerza de empuje una fuerza de flotación ($F_b$) generada por el l quido.

Cuando un objeto flota, la fuerza de empuje la fuerza de flotación ($F_b$) tiene que ser igual la fuerza gravitacional ($F_g$), lo que explica que no se hunda ni emerja.
(ID 11951)
Para explicar la sustentaci n experimentada por un cuerpo sumergido, es necesario estudiar las presiones verticales a las que est expuesto. Dado que la cara inferior del cuerpo se encuentra a una mayor profundidad que la cara superior, la presi n en la parte inferior es mayor que en la parte superior, lo que resulta en una fuerza neta hacia arriba que genera la sustentaci n observada. Este fen meno es similar cuando un cuerpo flota en la superficie, donde no hay presi n del agua sobre l; nuevamente, es la presi n en la parte inferior la que genera la sustentaci n.

Por lo tanto, en el caso en que el cuerpo est sumergido, se obtiene:
$\Delta p = p_2 - p_1 = \rho_w g h_2-\rho_w g h_1=\rho_w g (h_2 - h_1) = \rho_w g d$
O de manera similar en la superficie:
| $ \Delta p = \rho_w g d $ |
Finalmente, la fuerza de sustentaci n se obtiene utilizando la definici n de presi n, que para la presión en la base ($\Delta p$) con la fuerza de flotación ($F_b$) y la sección del cuerpo que flota ($S_s$) corresponde a:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
(ID 11952)
Un cuerpo flota si la fuerza de empuje la fuerza de flotación ($F_b$) es igual al peso del cuerpo la fuerza gravitacional ($F_g$):
| $ F_b = F_g $ |
Lo cual implica que la relaci n entre la masa del objeto que flota ($M_s$) y la masa de líquido desplazado ($M_b$) establece:
| $ M_b = M_s $ |
Lo cual corresponde al principio de Arqu medes [1].

que dice
Todo objeto flotante desplaza su propio peso en liquido.
![]() [1] "Peri ton ochoumenon" (Sobre cuerpos flotantes), Arqu medes, 287 a 212 a.C.
[1] "Peri ton ochoumenon" (Sobre cuerpos flotantes), Arqu medes, 287 a 212 a.C.
(ID 11956)
Dado que con la masa del objeto que flota ($M_s$) y la masa de líquido desplazado ($M_b$)
| $ M_b = M_s $ |
se relaciona con la densidad del objeto ($\rho_s$) y el volumen del objeto ($V_s$) por
| $ \rho_s \equiv\displaystyle\frac{ M_s }{ V_s }$ |
mientras que se cumple que con la densidad del líquido ($\rho_w$) y el volumen de lastre ($V_w$) tenemos
| $ M_b = \rho_w ( V_s + V_w )$ |
se obtiene la relaci n
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
De esta manera, un objeto con una densidad mayor que la del agua puede flotar siempre que tenga un volumen de aire por debajo del nivel de flotaci n (superficie del agua). En el caso de un barco, esto corresponde a los espacios que ocupan la carga y/o los pasajeros, mientras que en un submarino son los tanques de lastre, y en un pez es la vejiga natatoria.
Es importante destacar que:
Para un objeto sumergido, la suspensi n, ascenso o descenso no dependen de la profundidad en la que se encuentre. Sin embargo, la capacidad de bombear aire al tanque de lastre o vejiga natatoria s depende de la presi n circundante.
La densidad del agua no es homog nea en el mar, lo que hace que un objeto sumergido tenga que ajustar el volumen utilizado en el tanque de lastre o vejiga natatoria a medida que se desplaza.
(ID 15706)
Los submarinos y los peces tienen la capacidad de ajustar la profundidad a la que se mantienen en el agua. Pueden ascender hacia la superficie (flotar) o descender, limitados solo por la presi n que pueden soportar. Esto lo logran mediante el uso de lastres (en submarinos) y vejigas natatorias (en peces), que son espacios donde se puede expandir el aire, ocupando as un mayor volumen de agua desplazada.
Para lograr esto, la igualdad entre la masa de líquido desplazado ($M_b$) y la masa del objeto que flota ($M_s$) se puede reescribir en funci n de la densidad del líquido ($\rho_w$), la densidad del objeto ($\rho_s$) y el volumen del objeto ($V_s$), lo que permite ajustar el volumen de lastre ($V_w$):
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
permitiendo que una de las dos sea igual o supere a la otra. En resumen, si se aumenta el volumen de lastre ($V_w$), se aumenta la sustentaci n y se asciende; si se reduce el volumen, se hunde. Si se mantiene el volumen igual, se mantienen en suspensi n.

Un estudio interesante sobre c mo las ballenas usan el rgano de espermaceti para controlar la flotabilidad mediante calor y grasas se puede leer en el estudio "Control de flotabilidad como funci n del rgano de espermaceti en el cachalote" de Malcolm R. Clarke, publicado en J.mar.bio.Ass U.K. (1978) 58, 27-71.
(ID 11958)
(ID 15482)
ID:(1609, 0)
