Causa de variación en salinidad
Definición 
Al analizar la salinidad y el balance entre la precipitación y la evaporación, se pueden observar las siguientes relaciones:
A: En áreas donde hay una mayor reducción de agua debido a una mayor tasa de evaporación en comparación con la lluvia, se observa una mayor salinidad. Esto se debe a que a medida que el agua se evapora, los minerales y las sales disueltas en el agua se concentran, lo que aumenta la salinidad en la zona. Esta situación ocurre en regiones áridas o semiáridas, donde la evaporación es alta y la precipitación es limitada.
B: Por otro lado, en áreas donde hay una mayor contribución de agua debido a una mayor tasa de lluvia en comparación con la evaporación, se observa una menor salinidad. Esto se debe a que la lluvia aporta agua fresca que diluye las sales y reduce la concentración de minerales disueltos en el suelo y los cuerpos de agua. Estas áreas suelen ser regiones con una alta precipitación o cercanas a fuentes de agua dulce, como ríos o lagos.
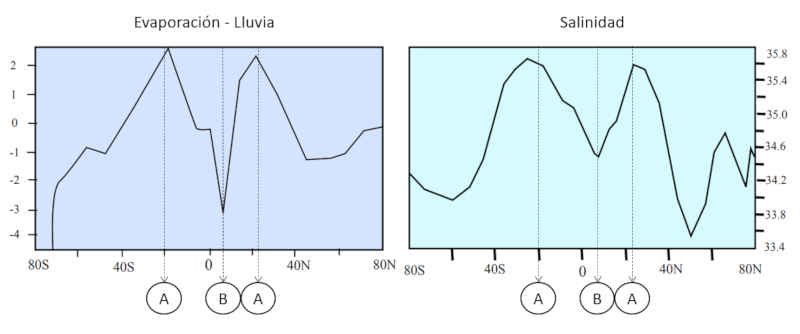
Esta imagen ilustra la relación entre la salinidad y el balance de lluvia y evaporación. En las áreas donde la evaporación es mayor que la lluvia, la salinidad tiende a ser alta, mientras que en las áreas donde la lluvia supera a la evaporación, la salinidad tiende a ser baja.
Es importante tener en cuenta que otros factores, como la geología, la circulación de aguas subterráneas y la presencia de corrientes oceánicas, también pueden influir en la salinidad de una región específica. Sin embargo, el balance entre la lluvia y la evaporación es un factor clave para comprender las variaciones de salinidad en diferentes áreas.
ID:(12370, 0)
Relación salinidad y temperatura
Imagen 
Si se miden la salinidad y las temperaturas en diferentes profundidades, se observa (en este caso, en una latitud de 9 grados sur) que la relación presenta dos puntos de inflexión:
- Desde la superficie hasta una profundidad de 800 m, se observa un aumento simultáneo de la temperatura y la salinidad.
- Si se continúa descendiendo hasta los 2000 m, la temperatura se mantiene mientras que la salinidad disminuye.
- Pasados los 2000 m, tanto la temperatura como la salinidad continúan aumentando con la profundidad.

Lo interesante es que los 4 grados en los que ocurre este comportamiento corresponden a la temperatura en la que el agua dulce alcanza su máxima densidad. Por ello, se puede interpretar el rango de 800 m a 2000 m como una profundidad en la que el agua 'expulsa la sal', similar a un cambio de fase. Para entender este comportamiento, es necesario primero estudiar cómo se comporta la entropía.
ID:(12371, 0)
Ecuación del estado simple del agua de mar
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
El coeficiente de expansi n t rmica esta definido mediante
Para el caso del agua oce nica se trabaja con el volumen espec fico
en vez del volumen $V$. Por ello se puede realizar un cambio de variable quedando el coeficiente de dilataci n t rmica como
El coeficiente de compresibilidad con $k_p$ esta definido mediante
Para el caso del agua oce nica se trabaja con el volumen espec fico
en vez del volumen $V$. Por ello se puede realizar un cambio de variable quedando el coeficiente de compresibilidad como
El signo negativo refleja que un aumento en la salinidad provoca un incremento en la densidad. Como el volumen específico es el inverso de la densidad, un aumento en la densidad implica necesariamente una disminución del volumen específico.
el coeficiente de contracción halina ($k_i$) adopta una forma análoga a el compresividad isotermica ($k_p$) y el coeficiente de dilatación térmica ($k_T$), en función de cómo el volumen ($V$) varía respecto de el salinidad ($i$), lo cual se define mediante:
En el contexto oceánico, utilizamos el volumen especifico ($\alpha$) en lugar de el volumen ($V$), definido a través de la siguiente expresión:
Por lo tanto, el coeficiente de contracción correspondiente debe expresarse de la siguiente forma:
La variaci n de la temperatura $T$ est regida por la ecuaci n del coeficiente de expansi n t rmica $k_T$:
La variaci n de la salinidad $i$ est regida por la ecuaci n del coeficiente de concentraci n de sal:
Finalmente, la variaci n de la presi n $p$ est regida por la ecuaci n del coeficiente de compresibilidad:
Por lo tanto, la variaci n total del volumen espec fico $\alpha$ se puede estimar como la suma de las variaciones individuales:
$d\alpha = d\alpha_T + d\alpha_s +d\alpha_p$
De esta manera, se puede generalizar la variaci n total como:
Ejemplos
Al analizar la salinidad y el balance entre la precipitaci n y la evaporaci n, se pueden observar las siguientes relaciones:
A: En reas donde hay una mayor reducci n de agua debido a una mayor tasa de evaporaci n en comparaci n con la lluvia, se observa una mayor salinidad. Esto se debe a que a medida que el agua se evapora, los minerales y las sales disueltas en el agua se concentran, lo que aumenta la salinidad en la zona. Esta situaci n ocurre en regiones ridas o semi ridas, donde la evaporaci n es alta y la precipitaci n es limitada.
B: Por otro lado, en reas donde hay una mayor contribuci n de agua debido a una mayor tasa de lluvia en comparaci n con la evaporaci n, se observa una menor salinidad. Esto se debe a que la lluvia aporta agua fresca que diluye las sales y reduce la concentraci n de minerales disueltos en el suelo y los cuerpos de agua. Estas reas suelen ser regiones con una alta precipitaci n o cercanas a fuentes de agua dulce, como r os o lagos.
Esta imagen ilustra la relaci n entre la salinidad y el balance de lluvia y evaporaci n. En las reas donde la evaporaci n es mayor que la lluvia, la salinidad tiende a ser alta, mientras que en las reas donde la lluvia supera a la evaporaci n, la salinidad tiende a ser baja.
Es importante tener en cuenta que otros factores, como la geolog a, la circulaci n de aguas subterr neas y la presencia de corrientes oce nicas, tambi n pueden influir en la salinidad de una regi n espec fica. Sin embargo, el balance entre la lluvia y la evaporaci n es un factor clave para comprender las variaciones de salinidad en diferentes reas.
Si se miden la salinidad y las temperaturas en diferentes profundidades, se observa (en este caso, en una latitud de 9 grados sur) que la relaci n presenta dos puntos de inflexi n:
- Desde la superficie hasta una profundidad de 800 m, se observa un aumento simult neo de la temperatura y la salinidad.
- Si se contin a descendiendo hasta los 2000 m, la temperatura se mantiene mientras que la salinidad disminuye.
- Pasados los 2000 m, tanto la temperatura como la salinidad contin an aumentando con la profundidad.
Lo interesante es que los 4 grados en los que ocurre este comportamiento corresponden a la temperatura en la que el agua dulce alcanza su m xima densidad. Por ello, se puede interpretar el rango de 800 m a 2000 m como una profundidad en la que el agua 'expulsa la sal', similar a un cambio de fase. Para entender este comportamiento, es necesario primero estudiar c mo se comporta la entrop a.
El problema de trabajar con el volumen en el caso del agua marina es que este depende de las variaciones de temperatura, salinidad y presi n. Por otro lado, la masa es menos sensible a dichas variaciones, por lo que tiene sentido trabajar con lo que llamamos el volumen espec fico, que se calcula dividiendo el volumen $V$ por la masa $M$:
$\displaystyle\frac{V}{M}$
Sin embargo, $M/V$ representa la densidad, por lo que el volumen espec fico se define como:
El coeficiente de dilatación térmica ($k_T$) presenta una forma similar a el compresividad isotermica ($k_p$) y el coeficiente de contracción halina ($k_i$). Sin embargo, en lugar de depender de ERROR:8848, asociado a la variación de la presión ($\Delta p$) o la variación del volumen especifico por cambio en la temperartura ($\Delta\alpha_T$), en este caso está vinculado a la derivada parcial de la volumen respecto de la salinidad a temperatura y presión constante ($\Delta V_{i,pT}$).
En el contexto oceánico, trabajamos con el volumen especifico ($\alpha$) en lugar de ERROR:8848. Por lo tanto, el coeficiente de contracción asociado debe expresarse de la siguiente manera:
El signo negativo refleja el hecho de que un aumento en la salinidad produce un incremento en la densidad. Dado que el volumen específico es el inverso de la densidad, un aumento en la densidad implica necesariamente una disminución del volumen específico.
En el caso del oc ano, se utiliza el concepto de volumen espec fico $\alpha$ en lugar del coeficiente de compresibilidad $k_p$. Por lo tanto, es necesario convertir el coeficiente de compresibilidad, que normalmente se define en funci n de la variaci n de volumen, en funci n de la variaci n del volumen espec fico. De esta manera, ante una variaci n de la presi n $p$, el coeficiente de compresi n en funci n del volumen espec fico $\alpha$ se puede expresar como:
El coeficiente de contracción halina ($k_i$) puede calcularse como la proporción entre la fracción la variación del volumen específico por cambios en la salinidad ($\Delta\alpha_i$) y el volumen especifico ($\alpha$) respecto de el salinidad ($i$), de modo que:
El volumen espec fico $\alpha$ var a en funci n de los cambios individuales de temperatura $T$, salinidad $i$ y presi n $p$. Si asumimos que el cambio total debido a variaciones simult neas en varias de estas variables se puede expresar como la suma de los cambios individuales:
La magnitud la variación del volumen especifico ($\Delta\alpha$) se puede calcular como la suma de la variación del volumen específico por cambios en la presión ($\Delta\alpha_p$), la variación del volumen específico por cambios en la salinidad ($\Delta\alpha_i$) y la variación del volumen especifico por cambio en la temperartura ($\Delta\alpha_T$), de acuerdo con la siguiente expresión:
ID:(1532, 0)
