Benützer:


Ursache für Schwankungen im Salzgehalt
Definition

Wenn man die Salinität und das Verhältnis von Niederschlag und Verdunstung analysiert, lassen sich folgende Zusammenhänge feststellen:

A: In Gebieten, in denen es aufgrund einer höheren Verdunstungsrate im Vergleich zum Niederschlag zu einem stärkeren Wasserverlust kommt, wird eine höhere Salinität beobachtet. Dies liegt daran, dass bei der Verdunstung das Wasser verdunstet, während die darin enthaltenen Mineralien und gelösten Salze konzentriert zurückbleiben, was zu einer erhöhten Salinität in der Region führt. Diese Situation tritt häufig in ariden oder halbariden Gebieten auf, in denen die Verdunstung hoch und der Niederschlag begrenzt ist.

B: Andererseits wird in Gebieten, in denen der Niederschlag im Vergleich zur Verdunstung höher ist, eine geringere Salinität beobachtet. Dies liegt daran, dass der Regen frisches Wasser bringt, das die Salze verdünnt und die Konzentration der gelösten Mineralien im Boden und in den Gewässern verringert. Diese Gebiete sind in der Regel Regionen mit hohem Niederschlag oder in der Nähe von Süßwasserquellen wie Flüssen oder Seen.

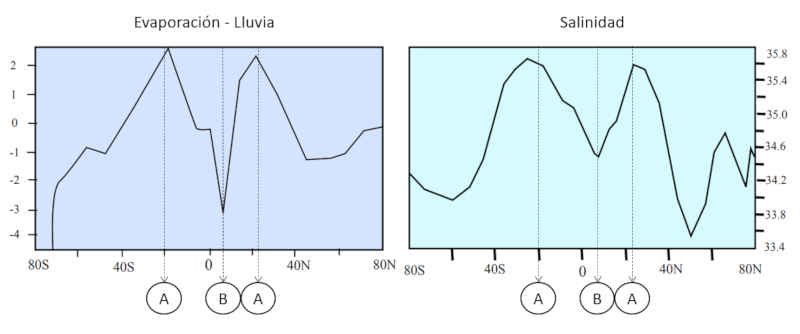
Dieses Bild verdeutlicht die Beziehung zwischen Salinität und dem Verhältnis von Niederschlag und Verdunstung. In Gebieten, in denen die Verdunstung den Niederschlag übersteigt, ist die Salinität tendenziell hoch, während in Gebieten, in denen der Niederschlag die Verdunstung übersteigt, die Salinität tendenziell niedrig ist.

Es ist wichtig zu beachten, dass auch andere Faktoren wie Geologie, Grundwasserzirkulation und Meeresströmungen die Salinität in bestimmten Regionen beeinflussen können. Das Verhältnis von Niederschlag und Verdunstung ist jedoch ein entscheidender Faktor, um die Variationen der Salinität in verschiedenen Gebieten zu verstehen.

ID:(12370, 0)


Beziehung zwischen Salzgehalt und Temperatur
Bild

Wenn Salinität und Temperaturen in verschiedenen Tiefen gemessen werden, zeigt sich (in diesem Fall bei einer Breitengrad von 9 Grad Süd), dass die Beziehung zwei Wendepunkte aufweist:

- Von der Oberfläche bis zu einer Tiefe von 800 m beobachtet man einen gleichzeitigen Anstieg von Temperatur und Salinität.
- Bei weiterem Abstieg bis zu einer Tiefe von 2000 m bleibt die Temperatur konstant, während die Salinität abnimmt.
- Jenseits von 2000 m steigen Temperatur und Salinität mit zunehmender Tiefe weiter an.

Interessanterweise liegen die 4 Grad, in denen dieses Verhalten auftritt, in dem Temperaturbereich, in dem Süßwasser seine maximale Dichte erreicht. Man kann daher den Bereich von 800 m bis 2000 m als eine Tiefe interpretieren, in der das Wasser 'Salz abgibt', ähnlich einem Phasenübergang. Um dieses Verhalten zu verstehen, muss man zuerst das Verhalten der Entropie analysieren.

ID:(12371, 0)


Gleichung des einfachen Zustands des Meerwassers
Beschreibung

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$k_i$
k_i
Coeficiente de contracción halina
-
$k_p$
k_p
Compresividad isotermica
1/Pa
$\rho$
rho
Densidad
kg/m^3
$\Delta p$
Dp
Druckschwankungen
Pa
$k_T$
k_T
Koeffizient der thermischen Ausdehnung
1/K
$\Delta V_{i,pT}$
DV_i_pT
Partielle Ableitung des Volumens in Bezug auf den Salzgehalt bei konstanter Temperatur und konstantem Druck
m^3
$\Delta T$
DT
Temperaturschwankungen
K
$dp$
dp
Variación de la presión
Pa
$di$
di
Variación de la salinidad
-
$dT$
dT
Variación de la temperatura
K
$d\alpha$
dalpha
Variación del volumen especifico
m^3/kg
$\Delta\alpha$
Dalpha
Variation des spezifischen Volumens
m^3/kg
$\Delta\alpha_p$
Dalpha_p
Variation des spezifischen Volumens aufgrund von Druckänderungen
m^3/kg
$\Delta\alpha_i$
Dalpha_i
Variation des spezifischen Volumens aufgrund von Salzgehaltänderung
m^3/kg
$\Delta\alpha_T$
Dalpha_T
Variation des spezifischen Volumens aufgrund von Temperaturänderungen
m^3/kg
$\alpha$
alpha
Volumen especifico
m^3/kg
$\alpha_0$
alpha_0
Volumen especifico base
m^3/kg

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Der thermische Ausdehnungskoeffizient ist definiert durch

$ k_T = +\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial T }\displaystyle\right)_ p $



Im Fall von ozeanischem Wasser arbeiten wir mit dem spezifischen Volumen

$ \alpha = \displaystyle\frac{1}{ \rho }$



anstelle des Volumens $V$. Daher kann eine Variablentransformation durchgef hrt werden, wodurch der thermische Ausdehnungskoeffizient wie folgt lautet:

$ k_T =\displaystyle\frac{1}{ \alpha_T }\left(\displaystyle\frac{ \partial\alpha_T }{ \partial T }\right)_{ p , i }$

.

(ID 11980)

Der Kompressibilit tskoeffizient mit $k_p$ ist definiert durch

$ k_p = -\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial p }\displaystyle\right)_ T $



Im Fall von ozeanischem Wasser arbeiten wir mit dem spezifischen Volumen

$ \alpha = \displaystyle\frac{1}{ \rho }$



anstelle des Volumens $V$. Daher kann eine Variablentransformation durchgef hrt werden, wodurch der Kompressibilit tskoeffizient wie folgt lautet:

$ k_p = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial p }\right)_{ T , S }$

.

(ID 11981)

Das negative Vorzeichen spiegelt wider, dass eine Erhöhung des Salzgehalts zu einer Erhöhung der Dichte führt. Da das spezifische Volumen der Kehrwert der Dichte ist, führt eine Erhöhung der Dichte zwangsläufig zu einer Verringerung des spezifischen Volumens.

der Coeficiente de contracción halina ($k_i$) hat eine ähnliche Form wie der Compresividad isotermica ($k_p$) und der Koeffizient der thermischen Ausdehnung ($k_T$), entsprechend der Art und Weise, wie sich der Volumen ($V$) in Abhängigkeit von der Salinidad ($i$) verändert, definiert durch:

$ k_i = -\displaystyle\frac{1}{ V }\displaystyle\left(\displaystyle\frac{\partial V }{\partial i }\displaystyle\right)_ { p , T } $



Im ozeanographischen Kontext verwenden wir der Volumen especifico ($\alpha$) anstelle von der Volumen ($V$), wie definiert durch:

$ \alpha = \displaystyle\frac{1}{ \rho }$



Daher sollte der entsprechende Kontraktionskoeffizient wie folgt ausgedrückt werden:

$ k_i = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha_i }{ \partial i }\right)_{ p , T }$

(ID 11982)

Die Variation der Temperatur $T$ wird durch die Gleichung des thermischen Ausdehnungskoeffizienten $k_T$ geregelt:

$ k_T =\displaystyle\frac{1}{ \alpha_T }\left(\displaystyle\frac{ \partial\alpha_T }{ \partial T }\right)_{ p , i }$



Die Variation der Salinit t $i$ wird durch die Gleichung des Salzkonzentrationskoeffizienten geregelt:

$ k_i = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha_i }{ \partial i }\right)_{ p , T }$



Schlie lich wird die Variation des Drucks $p$ durch die Gleichung des Kompressibilit tskoeffizienten geregelt:

$ k_p = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial p }\right)_{ T , S }$



Daher kann die Gesamtvariation des spezifischen Volumens $\alpha$ als Summe der individuellen Variationen gesch tzt werden:

$d\alpha = d\alpha_T + d\alpha_i +d\alpha_p$



Somit kann die Gesamtvariation verallgemeinert werden als:

$ \displaystyle\frac{ d\alpha }{ \alpha }= k_T dT - k_i di - k_p dp$

(ID 11983)

Beispiele

Wenn man die Salinit t und das Verh ltnis von Niederschlag und Verdunstung analysiert, lassen sich folgende Zusammenh nge feststellen:

A: In Gebieten, in denen es aufgrund einer h heren Verdunstungsrate im Vergleich zum Niederschlag zu einem st rkeren Wasserverlust kommt, wird eine h here Salinit t beobachtet. Dies liegt daran, dass bei der Verdunstung das Wasser verdunstet, w hrend die darin enthaltenen Mineralien und gel sten Salze konzentriert zur ckbleiben, was zu einer erh hten Salinit t in der Region f hrt. Diese Situation tritt h ufig in ariden oder halbariden Gebieten auf, in denen die Verdunstung hoch und der Niederschlag begrenzt ist.

B: Andererseits wird in Gebieten, in denen der Niederschlag im Vergleich zur Verdunstung h her ist, eine geringere Salinit t beobachtet. Dies liegt daran, dass der Regen frisches Wasser bringt, das die Salze verd nnt und die Konzentration der gel sten Mineralien im Boden und in den Gew ssern verringert. Diese Gebiete sind in der Regel Regionen mit hohem Niederschlag oder in der N he von S wasserquellen wie Fl ssen oder Seen.

Dieses Bild verdeutlicht die Beziehung zwischen Salinit t und dem Verh ltnis von Niederschlag und Verdunstung. In Gebieten, in denen die Verdunstung den Niederschlag bersteigt, ist die Salinit t tendenziell hoch, w hrend in Gebieten, in denen der Niederschlag die Verdunstung bersteigt, die Salinit t tendenziell niedrig ist.

Es ist wichtig zu beachten, dass auch andere Faktoren wie Geologie, Grundwasserzirkulation und Meeresstr mungen die Salinit t in bestimmten Regionen beeinflussen k nnen. Das Verh ltnis von Niederschlag und Verdunstung ist jedoch ein entscheidender Faktor, um die Variationen der Salinit t in verschiedenen Gebieten zu verstehen.

(ID 12370)

Wenn Salinit t und Temperaturen in verschiedenen Tiefen gemessen werden, zeigt sich (in diesem Fall bei einer Breitengrad von 9 Grad S d), dass die Beziehung zwei Wendepunkte aufweist:

- Von der Oberfl che bis zu einer Tiefe von 800 m beobachtet man einen gleichzeitigen Anstieg von Temperatur und Salinit t.
- Bei weiterem Abstieg bis zu einer Tiefe von 2000 m bleibt die Temperatur konstant, w hrend die Salinit t abnimmt.
- Jenseits von 2000 m steigen Temperatur und Salinit t mit zunehmender Tiefe weiter an.

Interessanterweise liegen die 4 Grad, in denen dieses Verhalten auftritt, in dem Temperaturbereich, in dem S wasser seine maximale Dichte erreicht. Man kann daher den Bereich von 800 m bis 2000 m als eine Tiefe interpretieren, in der das Wasser 'Salz abgibt', hnlich einem Phasen bergang. Um dieses Verhalten zu verstehen, muss man zuerst das Verhalten der Entropie analysieren.

(ID 12371)

Das Problem bei der Arbeit mit dem Volumen im Fall von Meerwasser ist, dass es von den Variationen in Temperatur, Salinit t und Druck abh ngt. Auf der anderen Seite ist die Masse weniger anf llig f r diese Variationen, daher macht es Sinn, mit dem sogenannten spezifischen Volumen zu arbeiten, das durch die Division des Volumens $V$ durch die Masse $M$ berechnet wird:

$\displaystyle\frac{V}{M}$



Allerdings repr sentiert $M/V$ die Dichte, daher wird das spezifische Volumen definiert als:

$ \alpha = \displaystyle\frac{1}{ \rho }$

(ID 11984)

Im Falle des Ozeans wird das Konzept des spezifischen Volumens $\alpha$ anstelle des thermischen Ausdehnungskoeffizienten $k_T$ verwendet. Daher ist es notwendig, den thermischen Ausdehnungskoeffizienten, der normalerweise in Bezug auf die Volumen nderung definiert ist, in Bezug auf die nderung des spezifischen Volumens umzuwandeln. Somit kann f r eine Temperatur nderung $T$ der thermische Ausdehnungskoeffizient in Bezug auf das spezifische Volumen $\alpha$ wie folgt ausgedr ckt werden:

$ k_T =\displaystyle\frac{1}{ \alpha_T }\left(\displaystyle\frac{ \partial\alpha_T }{ \partial T }\right)_{ p , i }$

(ID 11980)

Im Falle des Ozeans wird das Konzept des spezifischen Volumens $\alpha$ anstelle des Kompressibilit tskoeffizienten $k_p$ verwendet. Daher ist es notwendig, den Kompressibilit tskoeffizienten, der normalerweise in Bezug auf die Volumen nderung definiert ist, in Bezug auf die spezifische Volumen nderung umzuwandeln. Somit kann bei einer Druck nderung $p$ der Kompressionskoeffizient in Bezug auf das spezifische Volumen $\alpha$ wie folgt ausgedr ckt werden:

$ k_p = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha }{ \partial p }\right)_{ T , S }$

(ID 11981)

Der Coeficiente de contracción halina ($k_i$) kann als Verhältnis zwischen dem Bruch die Variation des spezifischen Volumens aufgrund von Salzgehaltänderung ($\Delta\alpha_i$) und der Volumen especifico ($\alpha$) relativ zu der Salinidad ($i$) berechnet werden, und zwar wie folgt:

$ k_i = -\displaystyle\frac{1}{ \alpha }\left(\displaystyle\frac{ \partial\alpha_i }{ \partial i }\right)_{ p , T }$

(ID 11982)

Das spezifische Volumen $\alpha$ variiert in Abh ngigkeit von den individuellen nderungen der Temperatur $T$, Salinit t $i$ und Druck $p$. Wenn wir davon ausgehen, dass die Gesamt nderung aufgrund gleichzeitiger Variationen mehrerer Variablen als Summe der einzelnen nderungen ausgedr ckt werden kann:

$ \displaystyle\frac{ d\alpha }{ \alpha }= k_T dT - k_i di - k_p dp$

(ID 11983)

Die Größe die Variation des spezifischen Volumens ($\Delta\alpha$) kann als die Summe von die Variation des spezifischen Volumens aufgrund von Druckänderungen ($\Delta\alpha_p$), die Variation des spezifischen Volumens aufgrund von Salzgehaltänderung ($\Delta\alpha_i$) und die Variation des spezifischen Volumens aufgrund von Temperaturänderungen ($\Delta\alpha_T$) berechnet werden, gemäß der folgenden Gleichung:

$ \Delta\alpha = \Delta\alpha_p + \Delta\alpha_i + \Delta\alpha_T $

(ID 16235)

ID:(1532, 0)