Transporte de calor en la superficie
Definición 
Las radiaciones que llegan a la superficie del océano o que son emitidas desde ella se resumen en el siguiente gráfico:
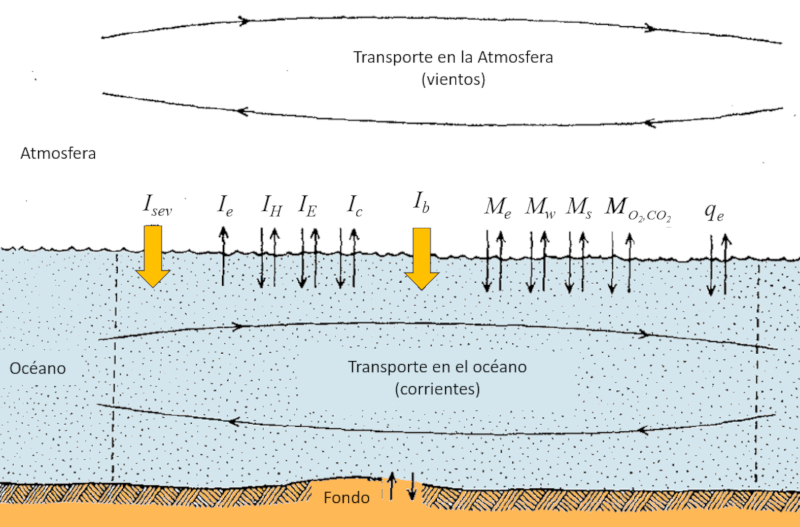
En resumen:
- $I_{sev}$: Radiación solar neta.
- $I_e$: Radiación emitida por la Tierra.
- $I_H$: Intercambio debido a la entrada/salida de gotas.
- $I_E$: Intercambio debido a la evaporación/condensación del agua.
- $I_c$: Intercambio debido a la conducción.
Este gráfico muestra de manera resumida las diferentes formas de radiación que interactúan en la superficie del océano y los intercambios de energía asociados.
ID:(13497, 0)
Rango de la radiación
Imagen 
La radiación se divide en dos tipos: la radiación del sol (principalmente visible) y la de la tierra (principalmente infrarroja). Si se representa en función de la longitud de onda, se obtiene:
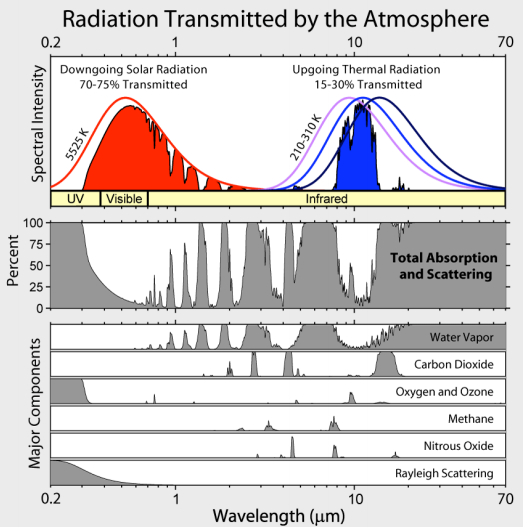
Rango de radiaciones (http://www.globalwarmingart.com/wiki)
Las mediciones típicas de los satélites, como las realizadas por el proyecto MODIS, se efectúan en diferentes canales.
La parte visible se mide con tres canales:
| Canales | Rangos [µm] | Pesos relativo |
| Blue | 0.459-0.479 | 0.4364 |
| Green | 0.545-0.565 | 0.2366 |
| Red | 0.620-0.670 | 0.3265 |
La parte infrarroja se estima con los siguientes canales:
| Canales | Rangos [µm] | Pesos relativo |
| NIR | 0.841-0.876 | 0.5447 |
| 1.2 | 1.230-1.250 | 0.1363 |
| 1.6 | 1.628-1.652 | 0.0469 |
| 2.1 | 2.105-2.155 | 0.2536 |
Los resultados del primer grupo se denominan VIS, mientras que los del segundo grupo se denominan NIR, aunque parte del espectro observado corresponde al rango visible.
Para entender por qué la separación se realiza en torno a los 750 nm en lugar de los 3 micrones, como normalmente se define el rango infrarrojo, es necesario considerar el comportamiento del albedo. Este muestra un aumento sustancial para longitudes de onda del orden de 750 nm y superiores, y no recién a partir de los 3 micrones (ver lámina del albedo en función de la longitud de onda).
ID:(9921, 0)
Flujo de radiación y transporte de energía desde la superficie
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Si la Tierra est a una temperatura $T_s$, emite radiaci n, principalmente con longitudes de onda $\lambda > 750$ nm, con una potencia dada por la ley de Stefan-Boltzmann:
donde $\sigma$ es la constante de Stefan-Boltzmann, $\epsilon$ es la emisividad y $S$ es la superficie de emisi n.
La intensidad de la radiaci n se define como la potencia por unidad de rea, por lo tanto, podemos expresarla como:
donde $S$ es el rea de emisi n.
Con ello la intensidad emitida desde la superficie de la Tierra $I_e$ es igual a
donde $T_e$ es la temperatura y $\epsilon$ es la emisividad de la superficie.
Dado que el flujo de evaporaci n se puede expresar como:
y queremos modelar el flujo como:
podemos determinar el factor constante como:
Ejemplos
Las radiaciones que llegan a la superficie del oc ano o que son emitidas desde ella se resumen en el siguiente gr fico:
En resumen:
- $I_{sev}$: Radiaci n solar neta.
- $I_e$: Radiaci n emitida por la Tierra.
- $I_H$: Intercambio debido a la entrada/salida de gotas.
- $I_E$: Intercambio debido a la evaporaci n/condensaci n del agua.
- $I_c$: Intercambio debido a la conducci n.
Este gr fico muestra de manera resumida las diferentes formas de radiaci n que interact an en la superficie del oc ano y los intercambios de energ a asociados.
La radiaci n se divide en dos tipos: la radiaci n del sol (principalmente visible) y la de la tierra (principalmente infrarroja). Si se representa en funci n de la longitud de onda, se obtiene:
Las mediciones t picas de los sat lites, como las realizadas por el proyecto MODIS, se efect an en diferentes canales.
La parte visible se mide con tres canales:
| Canales | Rangos [ m] | Pesos relativo |
| Blue | 0.459-0.479 | 0.4364 |
| Green | 0.545-0.565 | 0.2366 |
| Red | 0.620-0.670 | 0.3265 |
La parte infrarroja se estima con los siguientes canales:
| Canales | Rangos [ m] | Pesos relativo |
| NIR | 0.841-0.876 | 0.5447 |
| 1.2 | 1.230-1.250 | 0.1363 |
| 1.6 | 1.628-1.652 | 0.0469 |
| 2.1 | 2.105-2.155 | 0.2536 |
Los resultados del primer grupo se denominan VIS, mientras que los del segundo grupo se denominan NIR, aunque parte del espectro observado corresponde al rango visible.
Para entender por qu la separaci n se realiza en torno a los 750 nm en lugar de los 3 micrones, como normalmente se define el rango infrarrojo, es necesario considerar el comportamiento del albedo. Este muestra un aumento sustancial para longitudes de onda del orden de 750 nm y superiores, y no reci n a partir de los 3 micrones (ver l mina del albedo en funci n de la longitud de onda).
Si la Tierra est a una temperatura $T_e$, emite radiaci n de acuerdo con la ley de Stefan-Boltzmann con una intensidad dada por la siguiente f rmula:
donde $\sigma$ es la constante de Stefan-Boltzmann y $\epsilon$ es el coeficiente de emisividad. La constante de Stefan-Boltzmann $\sigma$ tiene un valor de aproximadamente $5.67 \times 10^{-8} W/m^2K^4$ y el coeficiente de emisividad $\epsilon$ representa la eficiencia con la que la superficie terrestre emite radiaci n, siendo un valor entre 0 y 1.
La energía transmitido por conducción y evaporación ($I_d$) depende de la diferencia entre la temperatura de la parte inferior de la atmósfera ($T_b$) y la temperatura de la superficie de la tierra ($T_e$), as como de la velocidad del viento ($u$) y las constantes el coeficiente de calor latente ($\kappa_l$) y el coeficiente de convección ($\kappa_c$), de la siguiente manera:
La superficie de la Tierra recibe energ a solar $I_{ev}$ y de la parte inferior de la atm sfera $I_b$. Toda esta energ a se irradia como $I_e$ y se pierde a trav s de convecci n y conducci n $I_d$ con:
El flujo de radiaci n debido a los elementos de transporte se expresa de la siguiente manera:
donde se puede demostrar que el coeficiente constante de evaporaci n tiene la forma:
Si asumimos una concentraci n molar del aire de $c_a\sim 42.4$, un calor latente molar de $L_v\sim 40.6,kJ/mol$, una velocidad del viento de $u_z\sim 8,m/s$, una constante de transporte de calor latente de $C_E\sim 5.0\times 10^{-4}$, una presi n de vapor de agua saturado de $p_{s,e}\sim 1519,Pa$, una humedad relativa de $RH_e\sim 85%$, una presi n atmosf rica de $p_a\sim 10^5,Pa$ y una cobertura visual de $\gamma_v\sim 42%$, la constante tiene un orden de magnitud de $\kappa_c\sim 5.66,J/m^3s$.
Dado que el flujo de transporte est dado por
y el flujo de evaporaci n es
y se busca modelar el flujo como
podemos determinar el factor de la temperatura como
Suponiendo que la densidad del aire es $\rho_a\sim 1.225,kg/m^3$, la concentraci n molar del aire es $c_a\sim 42.4$, el calor latente molar es $L_v\sim 40.6,kJ/mol$, la velocidad del viento es $u_z\sim 8,m/s$, la constante de transporte de calor es $C_H\sim 1.13\times 10^{-4}$ y la constante de transporte de calor latente es $C_E\sim 5.0\times 10^{-4}$, la presi n de vapor de agua saturado es $p_{s,e}\sim 1519,Pa$, la humedad relativa es $RH_e\sim 85%$, la presi n atmosf rica es $p_a\sim 10^5,Pa$ y la cobertura visible es $\gamma_v\sim 42%$, el incremento de flujo por grado de diferencia de temperatura es del orden de $\kappa_c\sim 0.47,J/m^3s,K$.
Adem s de la radiaci n infrarroja, existe un transporte de calor a trav s de la convecci n o el flujo de calor sensible (SHF). Ambos fen menos son, en primera aproximaci n, proporcionales a la diferencia de temperatura entre la Tierra $T_e$ y la parte inferior de la atm sfera $T_b$:
Si el flujo de calor t pico transportado por convecci n es del orden de $I_H\sim 17 W/m^2$, y considerando que la densidad es del orden de $\rho_a\sim 1.225 kg/m^3$, la capacidad calor fica espec fica es $c_p\sim 1006.43 J/kg K$, y la velocidad del viento es del orden de $u_z\sim 8 m/s$, entonces, con una diferencia de temperatura de $T_e-T_b\sim 15.2 K$, el coeficiente de transferencia de calor es del orden de $C_H\sim 1.13\times 10^{-4}$.
Dado que la concentraci n molar $c_a$ es proporcional a la presi n $p_a$ seg n:
podemos reescribir
como
ID:(1753, 0)
