Benützer:
Wärmetransport an der Oberfläche
Definition 
Die Strahlungen, die die Oberfläche des Ozeans erreichen oder von ihr abgegeben werden, lassen sich in der folgenden Grafik zusammenfassen:
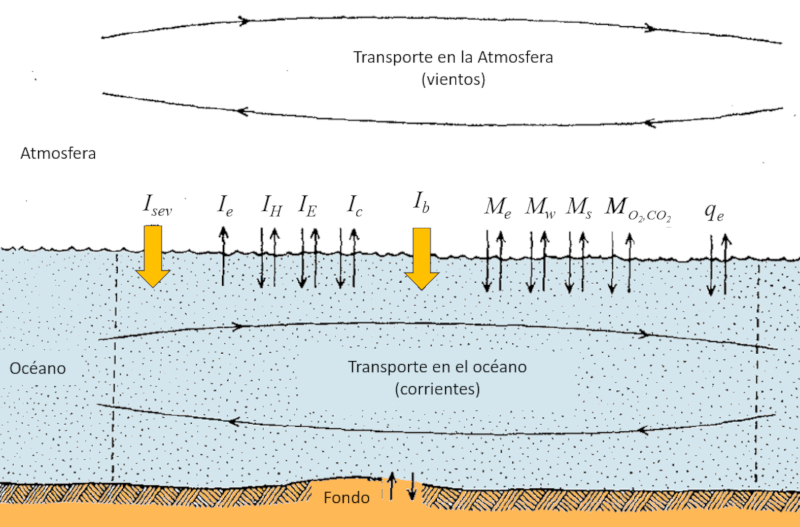
Zusammenfassend:
- $I_{sev}$: Netto-Sonnenstrahlung.
- $I_e$: Von der Erde abgegebene Strahlung.
- $I_H$: Austausch aufgrund von Ein-/Ausgang von Wassertropfen.
- $I_E$: Austausch aufgrund von Wasser verdampfung/Kondensation.
- $I_c$: Austausch aufgrund von Wärmeleitung.
Diese Grafik gibt einen zusammenfassenden Überblick über die verschiedenen Formen der Strahlung, die an der Oberfläche des Ozeans interagieren, sowie über die damit verbundenen Energieaustausche.
ID:(13497, 0)
Flujo de radiación y trasporte de energía desde la superficie
Beschreibung
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Wenn die Erde eine Temperatur von $T_s$ hat, emittiert sie Strahlung, haupts chlich bei Wellenl ngen $\lambda > 750$ nm, mit einer Leistung, die durch das Stefan-Boltzmann-Gesetz gegeben ist:
| $ P = \sigma \epsilon S T_s ^4$ |
Hierbei ist $\sigma$ die Stefan-Boltzmann-Konstante, $\epsilon$ die Emissionsf higkeit und $S$ die Strahlungsfl che.
Die Intensit t der Strahlung wird als Leistung pro Fl che definiert, daher k nnen wir sie wie folgt ausdr cken:
| $ I =\displaystyle\frac{ P }{ S }$ |
Hierbei ist $S$ die Fl che der Strahlung.
Die von der Oberfl che der Erde emittierte Intensit t $I_e$ wird daher durch folgende Gleichung beschrieben:
| $ I_e = \epsilon \sigma T_e ^4 $ |
Hierbei ist $T_e$ die Temperatur und $\epsilon$ die Emissionsf higkeit der Oberfl che.
(ID 4676)
Da der Verdampfungsfluss wie folgt ausgedr ckt werden kann:
| $I_E=c_aL_vC_Eu_z\displaystyle\frac{(p_{v,e}-p_{v,a})}{p_a}$ |
und wir den Fluss wie folgt modellieren m chten:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
k nnen wir den konstanten Faktor bestimmen als:
| $ \kappa_l = L_v C_E \displaystyle\frac{ p_{s,e} }{ R T_e }( RH_e - \gamma_v )$ |
(ID 9271)
Beispiele
Die Strahlungen, die die Oberfl che des Ozeans erreichen oder von ihr abgegeben werden, lassen sich in der folgenden Grafik zusammenfassen:
Zusammenfassend:
- $I_{sev}$: Netto-Sonnenstrahlung.
- $I_e$: Von der Erde abgegebene Strahlung.
- $I_H$: Austausch aufgrund von Ein-/Ausgang von Wassertropfen.
- $I_E$: Austausch aufgrund von Wasser verdampfung/Kondensation.
- $I_c$: Austausch aufgrund von W rmeleitung.
Diese Grafik gibt einen zusammenfassenden berblick ber die verschiedenen Formen der Strahlung, die an der Oberfl che des Ozeans interagieren, sowie ber die damit verbundenen Energieaustausche.
(ID 13497)
Die Strahlung wird in die des Sonnenlichts ( berwiegend sichtbar) und die der Erde ( berwiegend infrarot) unterteilt. Wenn man sie als Funktion der Wellenl nge darstellt, erh lt man folgendes Bild:
Typische Satellitenmessungen, wie sie beispielsweise im MODIS-Projekt durchgef hrt werden, erfolgen in verschiedenen Kan len.
Der sichtbare Teil wird mit drei Kan len gemessen:
| Kan le | Bereiche [ m] | Relative Gewichte |
| Blau | 0.459-0.479 | 0.4364 |
| Gr n | 0.545-0.565 | 0.2366 |
| Rot | 0.620-0.670 | 0.3265 |
Der infrarote Teil wird mit den folgenden Kan len gesch tzt:
| Kan le | Bereiche [ m] | Relative Gewichte |
| NIR | 0.841-0.876 | 0.5447 |
| 1.2 | 1.230-1.250 | 0.1363 |
| 1.6 | 1.628-1.652 | 0.0469 |
| 2.1 | 2.105-2.155 | 0.2536 |
Die Ergebnisse der ersten Gruppe werden als VIS bezeichnet, w hrend die der zweiten Gruppe als NIR bezeichnet werden, obwohl ein Teil des beobachteten Spektrums in den sichtbaren Bereich f llt.
Um zu verstehen, warum die Trennung bei etwa 750 nm und nicht bei 3 Mikrometern erfolgt, wie es normalerweise f r den Infrarotbereich definiert ist, muss man das Verhalten des Albedos betrachten. Dieses zeigt einen deutlichen Anstieg f r Wellenl ngen im Bereich von 750 nm und dar ber, nicht erst ab 3 Mikrometern (siehe Albedo-Diagramm in Abh ngigkeit von der Wellenl nge).
(ID 9921)
ID:(1753, 0)