Utilizador:
Pressão sonora
Descrição
À medida que o som se propaga, ele provoca o deslocamento das moléculas na borda do sistema, levando a impactos contra a parede. Esses impactos transferem momento para a parede, resultando em uma força. Como a força é gerada por um grande número de partículas, seu efeito depende da área de superfície do sistema, o que gera uma pressão.
É importante entender que a pressão sonora não é igual à pressão ambiente. No ar, esta última está na ordem de $10^5,Pa$, enquanto a pressão sonora geralmente é muito menor que $1,Pa$.
ID:(134, 0)
Formação de pressão
Descrição
Se deslocarmos a face de um cubo, geramos um aumento ou diminuição da concentração, o que leva a uma diminuição ou aumento das colisões das moléculas com a face do volume:
Como a pressão é a transferência de momento devido às colisões das moléculas com a parede, a variação do volume leva a um aumento ou diminuição da pressão.
ID:(1865, 0)
Pressão sonora
Descrição
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
A varia o do momento $dp$ est associada massa das mol culas $m$ e velocidade do som $u$ das mol culas atrav s de:
$dp = 2mu \approx mu$
Assim, em um intervalo de tempo igual ao per odo $dt \approx T$, temos:
$F=\displaystyle\frac{dp}{dt}=\displaystyle\frac{mu}{T}$
Portanto, la pressão sonora ($p_s$) pode ser calculado usando a press o
| $$ |
la concentração molar ($c$)
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
e o volume com moléculas ($\Delta V$) que varia
| $ \Delta V = S \lambda $ |
da seguinte forma:
$p=\displaystyle\frac{1}{S} \displaystyle\frac{dp}{dt}=\displaystyle\frac{1}{S}\displaystyle\frac{mu}{T}=\displaystyle\frac{muc}{ScT}=\displaystyle\frac{muc}{S\lambda}=\displaystyle\frac{muc}{\Delta V}=\rho u c$
No ltimo termo, tanto o numerador quanto o denominador s o multiplicados por $c$. A express o no denominador representa o volume do g s deslocado pelo som em $T$, ent o podemos substituir a massa dividida por este volume pela densidade, resultando em:
| $ p = \rho c u $ |
(ID 3391)
Como ERROR:5104 calculado a partir de la pressão sonora ($p_s$) e la velocidade da molécula ($u$) usando
| $ Z =\displaystyle\frac{ p }{ u }$ |
junto com a express o para la pressão sonora ($p_s$) em termos de la densidade média ($\rho$) e la concentração molar ($c$),
| $ p = \rho c u $ |
n s obtemos
| $ Z = \rho c $ |
(ID 12413)
Exemplos
(ID 15458)
medida que o som se propaga, ele provoca o deslocamento das mol culas na borda do sistema, levando a impactos contra a parede. Esses impactos transferem momento para a parede, resultando em uma for a. Como a for a gerada por um grande n mero de part culas, seu efeito depende da rea de superf cie do sistema, o que gera uma press o.
importante entender que a press o sonora n o igual press o ambiente. No ar, esta ltima est na ordem de $10^5,Pa$, enquanto a press o sonora geralmente muito menor que $1,Pa$.
(ID 134)
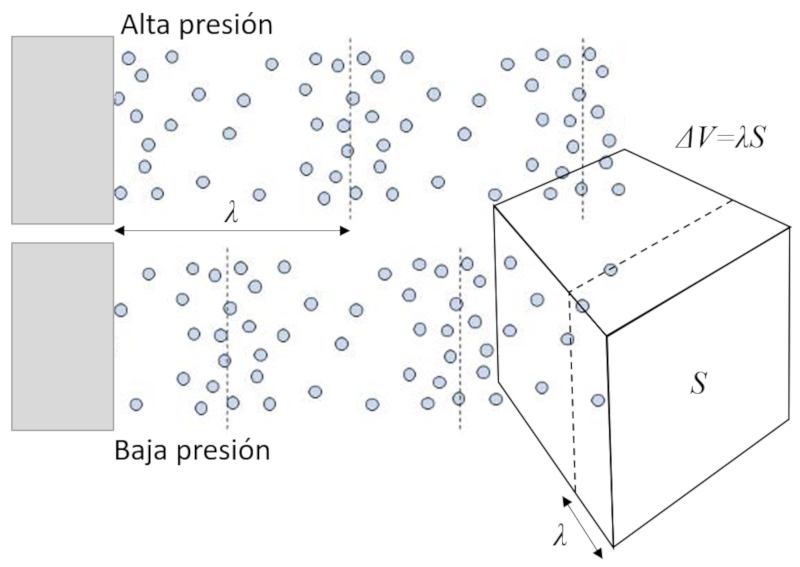
Se deslocarmos a face de um cubo, geramos um aumento ou diminui o da concentra o, o que leva a uma diminui o ou aumento das colis es das mol culas com a face do volume:
Como a press o a transfer ncia de momento devido s colis es das mol culas com a parede, a varia o do volume leva a um aumento ou diminui o da press o.
(ID 1865)
(ID 15453)
La pressão da coluna de água ($p$) calculado a partir de la força da coluna ($F$) e la altura da coluna líquida ($S$) da seguinte forma:
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
(ID 4342)
Quando uma onda sonora atravessa um volume com moléculas ($\Delta V$), ela se expande e contrai ao longo de uma dist ncia da ordem de um comprimento da onda sonora ($\lambda$), resultando em uma varia o de volume que depende de la seção ou superfície ($S$) perpendicular dire o de propaga o.
Portanto, a varia o de volume igual a:
| $ \Delta V = S \lambda $ |
(ID 3398)
La pressão sonora ($p_s$) pode ser entendido como a densidade de momento calculada a partir de la densidade média ($\rho$) e la velocidade da molécula ($u$), que ent o multiplicada por la concentração molar ($c$) atrav s de
| $ p = \rho c u $ |
(ID 3391)
La pressão de referência ($L$) abrange uma ampla gama de la pressão sonora ($p_s$), tornando til definir uma escala que mitigue essa dificuldade. Para isso, podemos trabalhar com o logaritmo da press o normalizado por um valor que corresponda a zero nesta escala. Se tomarmos a press o m nima que uma pessoa pode detectar, definida como la pressão de referência ($p_{ref}$), podemos definir uma escala usando:
| $ L = 20 \log_{10}\left(\displaystyle\frac{ p_s }{ p_{ref} }\right)$ |
que come a em 0 para o intervalo aud vel. No caso do ar, la pressão de referência ($p_{ref}$) de $20 \mu Pa$.
(ID 3407)
O conceito de ERROR:5104,0 fornece uma medida da resist ncia do sistema para transmitir a onda sonora. Ele considera uma press o atuante e estabelece uma medida na qual o meio exposto deslocado. Dessa forma, la pressão sonora ($p_s$) comparado com la velocidade da molécula ($u$).
Portanto, ERROR:5104 definido como:
| $ Z =\displaystyle\frac{ p }{ u }$ |
(ID 3414)
Para calcular ERROR:5104 a partir de la densidade média ($\rho$) e la concentração molar ($c$), utiliza-se a f rmula:
| $ Z = \rho c $ |
(ID 12413)
ID:(1589, 0)