Benützer:


Kreuzprodukt oder Vektorprodukt
Storyboard

Das sogenannte Kreuzprodukt oder Vektorprodukt ermöglicht die Bestimmung eines orthogonalen Vektors zu den Vektoren, die ihn erzeugen. Ihre Größe entspricht dem doppelten der Fläche, die ein Rechteck mit Seiten haben würde, die den Größen der einzelnen Vektoren entsprechen.

>Modell

ID:(1259, 0)


Grafische Darstellung des Kreuzproduktes
Definition

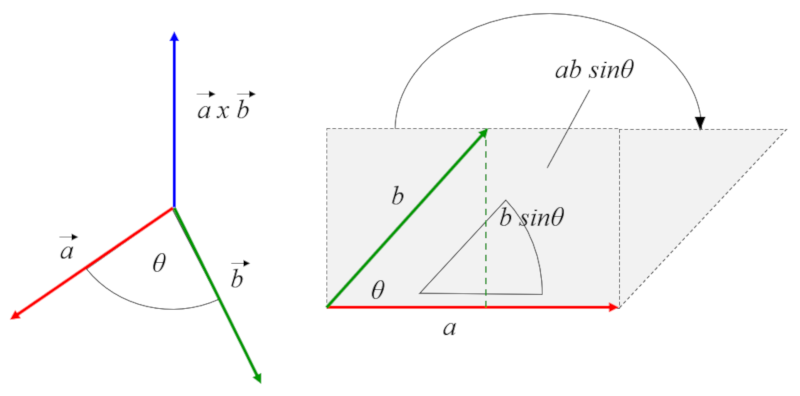
Das Kreuzprodukt erzeugt einen Vektor, der orthogonal zu denjenigen ist, die es erzeugen, und dessen Größe die Multiplikation der Größen jedes Vektors und des Sinus des Winkels zwischen ihnen ist.

Die Länge des resultierenden Vektors entspricht der Fläche des Parallelepipeds, die von den beiden Vektoren gebildet wird, die es erzeugen:

ID:(4582, 0)


Kreuzprodukt oder Vektorprodukt
Beschreibung

Das sogenannte Kreuzprodukt oder Vektorprodukt ermöglicht die Bestimmung eines orthogonalen Vektors zu den Vektoren, die ihn erzeugen. Ihre Größe entspricht dem doppelten der Fläche, die ein Rechteck mit Seiten haben würde, die den Größen der einzelnen Vektoren entsprechen.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$\theta$
theta
Angulo entre los vectores
rad
$\vec{a}$
&a
Komponente des Vektors $\vec{a}$ in $\hat{x}$
m
$\mid\vec{a}\mid$
a
Magnitud del vector
m
$\mid\vec{b}\mid$
b
Magnitud del vector
m
$\mid\vec{a}\times\vec{b}\mid$
axb
Produkt Cruz und Winkel
-
$\vec{b}$
&b
Vector
m
$b_y$
b_y
Vector que resulta de la suma
m

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

Das Kreuzprodukt erzeugt einen Vektor, der orthogonal zu denjenigen ist, die es erzeugen, und dessen Gr e die Multiplikation der Gr en jedes Vektors und des Sinus des Winkels zwischen ihnen ist.

Die L nge des resultierenden Vektors entspricht der Fl che des Parallelepipeds, die von den beiden Vektoren gebildet wird, die es erzeugen:

(ID 4582)

El producto cruz se puede definir como una determinante de una matriz cuyas lineas son los versores del sistema \hat{n}=(e_x,e_y,e_z), en la segunda y tercera l neas las coordenadas de los vectores \vec{a}=(a_x,a_y,a_z) y \vec{b}=(b_x,b_y,b_z) por lo que se obtiene un vector

$ \vec{a}\times\vec{b} =( a_y b_z - a_z b_y , a_z b_x - a_x b_z , a_x b_y - a_y b_x )$

(ID 3676)

Si se expresa el producto cruz en funci n del versor \hat{e} ortogonal a los vectores \vec{a} y \vec{b} se tiene que

$ \mid\vec{a}\times\vec{b}\mid = \mid\vec{a}\mid \mid\vec{b}\mid \sin \theta $

donde \theta es el angulo entre ambos vectores.

(ID 3677)

ID:(1259, 0)