Transporte de Calor
Storyboard 
El transporte de calor a través de un sistema compuesto por múltiples medios se puede estimar analizando cómo se conduce el calor en cada medio y cómo se transfiere en cada interfaz. El cálculo se realiza utilizando los parámetros específicos de cada medio e interfaz, así como las temperaturas en ambos extremos del sistema, proporcionando así las temperaturas en cada interfaz.
ID:(1483, 0)
Transporte de calor
Concepto 
El sistema básico incluye una transferencia generada por la diferencia de temperatura ($\Delta T$), que consta de la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$). Por lo tanto:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Con la tasa de flujo de calor ($q$) siendo el responsable de la transferencia entre el interior y el conductor, mediante el coeficiente de transmisión interno ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
La conducción involucra a la conductividad térmica ($\lambda$) y el largo del conductor ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Y la transferencia del conductor al exterior, con el coeficiente de transmisión externo ($\alpha_e$) se representa por:
| $ q = \alpha_e \Delta T_e $ |
Todo esto está representado gráficamente por:
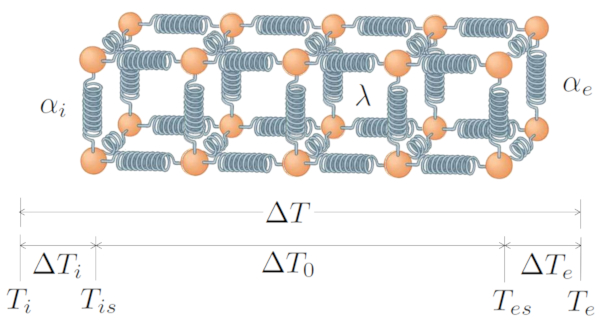
Transferencia de calor
ID:(7723, 0)
Transporte de calor entre dos sistemas vía un tercero medio
Concepto 
La tasa de flujo de calor ($q$) se calcula a partir de el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) y la diferencia de temperatura ($\Delta T$) utilizando la siguiente fórmula:
| $ q = k \Delta T $ |
donde el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) se obtiene a partir de el coeficiente de transmisión externo ($\alpha_e$), el coeficiente de transmisión interno ($\alpha_i$), la conductividad térmica ($\lambda$) y el largo del conductor ($L$) mediante la ecuación:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
Esto se ilustra en la siguiente imagen:
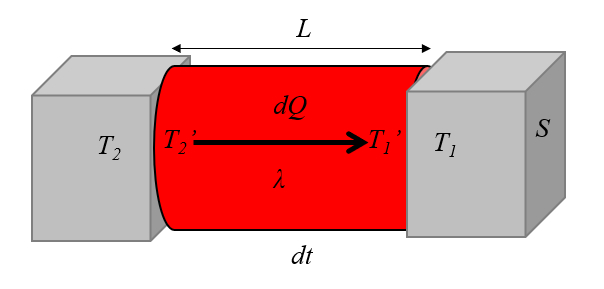
ID:(1675, 0)
Perfil de Temperatura
Concepto 
Por lo general, la variación de la temperatura dentro de un conductor es lineal. Sin embargo, en el caso de medios gaseosos y/o líquidos en contacto con el conductor, se produce una gradual variación de la temperatura desde el centro del medio hasta la superficie, como se representa en la siguiente imagen:
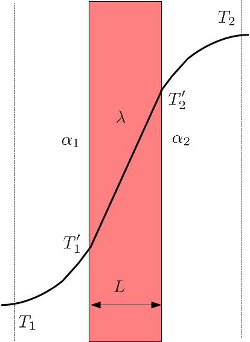
Perfil de temperatura alrededor de un conductor solido
la temperatura en la superficie exterior ($T_{es}$) depende de la temperatura exterior ($T_e$), el coeficiente de total de transporte ($k$), el coeficiente de transmisión externo ($\alpha_e$) y la diferencia de temperatura ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
la temperatura en la superficie interior ($T_{is}$) es una función de la temperatura en el interior ($T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
y la diferencia de temperatura ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
ID:(7722, 0)
Transporte total del flujo de calor
Concepto 
Cuando el material incluye múltiples conductores conectados en serie, el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) se calcula a partir de el coeficiente de transmisión externo ($\alpha_e$), el coeficiente de transmisión interno ($\alpha_i$), la conductividad térmica elemento i ($\lambda_i$) y el largo elemento i ($L_i$) utilizando la ecuación:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
Este proceso se ilustra en el diagrama siguiente:

Transporte por un medio
ID:(7721, 0)
