Wärmetransport
Storyboard 
Der Wärmetransport durch ein System, das aus mehreren Medien besteht, kann geschätzt werden, indem analysiert wird, wie die Wärme in jedem Medium geleitet und an jeder Schnittstelle übertragen wird. Die Berechnung erfolgt unter Verwendung der spezifischen Parameter jedes Mediums und jeder Schnittstelle sowie der Temperaturen an beiden Enden des Systems, wodurch die Temperaturen an jeder Schnittstelle ermittelt werden.
ID:(1483, 0)
Wärmetransport
Bild 
Das grundlegende System umfasst eine Übertragung, die durch die Temperaturdifferenz ($\Delta T$) generiert wird und aus die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) besteht. Daher:
Mit die Wärmestromrate ($q$) als Verantwortlichem für die Übertragung zwischen dem Inneren und dem Leiter, verwendet der Interner Übertragungskoeffizient ($\alpha_i$):
Die Leitung betrifft die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$):
Und der Transfer vom Leiter nach außen, mit der Externer Transmissionskoeffizient ($\alpha_e$), wird dargestellt durch:
All dies wird grafisch dargestellt durch:
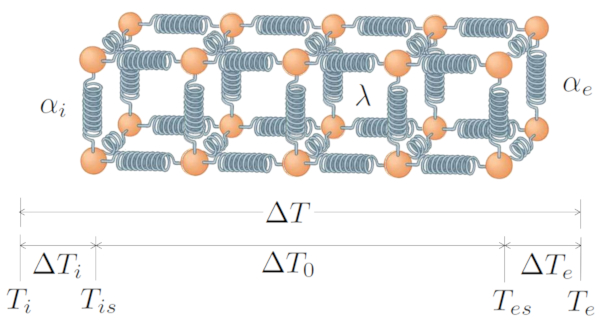
ID:(7723, 0)
Wärmetransport zwischen zwei Systemen über einen Drittmittel
Notiz 
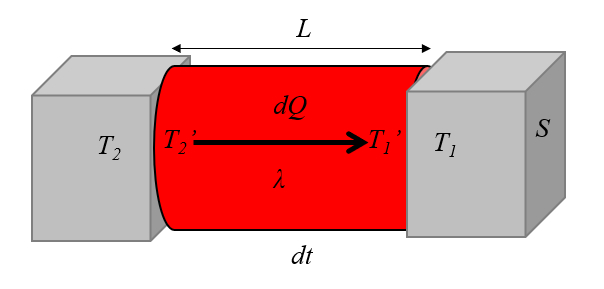
Die Wärmestromrate ($q$) wird aus der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) und die Temperaturdifferenz ($\Delta T$) mittels folgender Gleichung berechnet:
wobei der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) aus der Externer Transmissionskoeffizient ($\alpha_e$), der Interner Übertragungskoeffizient ($\alpha_i$), die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$) mit dieser Gleichung abgeleitet wird:
Dies wird in folgendem Bild dargestellt:
ID:(1675, 0)
Temperaturprofil
Zitat 
In der Regel variiert die Temperatur innerhalb eines Leiters linear. Dies gilt jedoch nicht für gasförmige und/oder flüssige Medien, die mit dem Leiter in Kontakt stehen. In diesem Fall gibt es eine allmähliche Temperaturänderung von der Mitte des Mediums zur Oberfläche, wie in folgender Abbildung dargestellt:
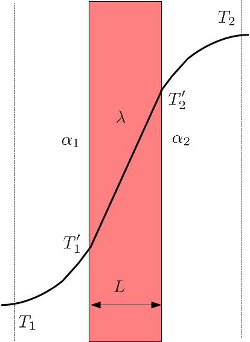
die Äußere Oberflächentemperatur ($T_{es}$) hängt ab von die Außentemperatur ($T_e$), der Koeffizient Gesamttransportation ($k$), der Externer Transmissionskoeffizient ($\alpha_e$) und die Temperaturdifferenz ($\Delta T$):
die Innenoberflächentemperatur ($T_{is}$) ist eine Funktion von die Innentemperatur ($T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$):
und die Temperaturdifferenz ($\Delta T$):
ID:(7722, 0)
Transport des gesamten Wärmeflusses
Übung 
Wenn das Material mehrere in Serie geschaltete Leiter enthält, wird der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) aus der Externer Transmissionskoeffizient ($\alpha_e$), der Interner Übertragungskoeffizient ($\alpha_i$), die Wärmeleitelement i ($\lambda_i$) und der Elementlänge i ($L_i$) mittels der Gleichung berechnet:
Dieser Prozess wird im folgenden Diagramm dargestellt:

ID:(7721, 0)
