O ciclo Stirling envolve quatro fases principais: aquecimento, expans o, resfriamento e compress o, conduzidas em um ambiente selado onde um g s como h lio ou hidrog nio atua como fluido de trabalho.

Durante a fase de aquecimento, o g s aquecido a volume constante, absorvendo calor de uma fonte externa, o que aumenta sua temperatura e press o. Isso seguido pela fase de expans o, onde o g s aquecido se expande e realiza trabalho sobre um pist o ou outro mecanismo, reduzindo sua temperatura e press o, mas convertendo o calor em energia mec nica.

Em seguida, ocorre a fase de resfriamento a volume constante. Aqui, o g s perde calor, o que diminui sua temperatura e press o, preparando-o para a fase final. O regenerador desempenha um papel cr tico ao absorver calor do g s, o que conserva energia e melhora a efici ncia.

O ciclo conclui com a compress o do g s resfriado, que requer menos energia do que a produzida durante a expans o. Essa compress o aumenta a temperatura do g s, embora n o tanto quanto na fase inicial de aquecimento, e o ciclo come a novamente.

O regenerador vital durante todo esse processo, armazenando calor da fase de resfriamento e devolvendo-o durante o aquecimento, reutilizando assim a energia dentro do sistema e aumentando significativamente a efici ncia t rmica do motor. Os motores Stirling s o valorizados por sua opera o silenciosa e pela flexibilidade de usar qualquer fonte de calor, tornando-os adapt veis e ben ficos ambientalmente para diversas aplica es.

mechanisms

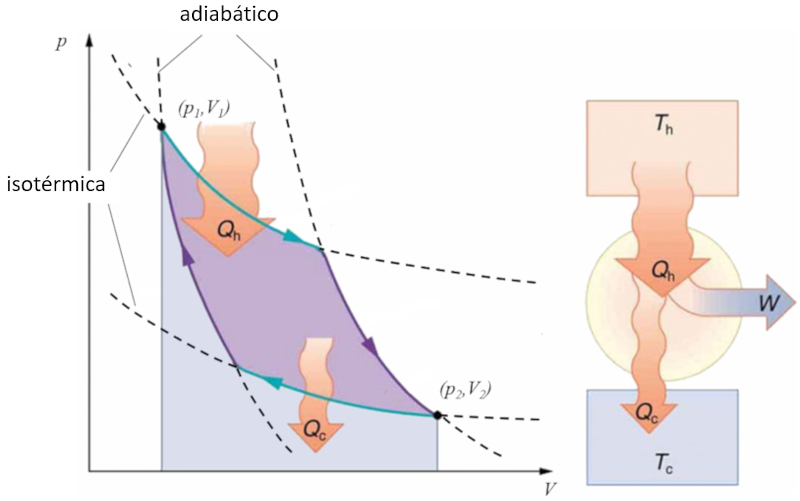
Sadi Carnot introduziu [1] o conceito te rico do primeiro projeto de m quina capaz de gerar trabalho mec nico com base em um gradiente de temperatura. Isso alcan ado por meio de um processo no espa o press o-volume, onde calor adicionado e extra do, conforme ilustrado na imagem:

image

A rea sob a curva o calor fornecido ($Q_H$), que se estende de 1 a 2, representa a energia necess ria para transitar do estado ($p_1, V_1$) para o estado ($p_2, V_2$). Por outro lado, a rea sob a curva o calor absorvido ($Q_C$), indo de 2 para 1, representa a extra o de energia necess ria para retornar do estado ($p_2, V_2$) ao estado ($p_1, V_1$). A diferen a entre essas reas corresponde regi o delimitada por ambas as curvas e representa o trabalho eficaz ($W$) que o sistema pode realizar.

Carnot tamb m demonstrou que, de acordo com a segunda lei da termodin mica, o calor fornecido ($Q_H$) n o pode ser igual a zero. Isso implica que n o existem m quinas capazes de converter todo o calor em trabalho.

[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflex es sobre a Pot ncia Motriz do Fogo e sobre M quinas Adequadas para Desenvolver Essa Pot ncia), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)

O ciclo Stirling [1] pode ser considerado uma solu o t cnica baseada no ciclo de Carnot, que consiste em quatro etapas bem definidas:

Fase 1 para 2: Compress o isoterma $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_1)$.
Fase 2 para 3: Aquecimento isoc rico $(p_2,V_2,T_1)\rightarrow(p_3,V_2,T_2)$.
Fase 3 para 4: Expans o isoterma $(p_3,V_2,T_2)\rightarrow(p_4,V_1,T_2)$.
Fase 4 para 1: Resfriamento isoc rico $(p_4,V_1,T_2)\rightarrow(p_1,V_1,T_1)$.

importante destacar que esse ciclo n o envolve uma fase adiab tica; em vez disso, ele se baseia na troca entre processos isoc ricos (a volume constante) e processos isot rmicos (a temperatura constante).

Essas fases podem ser visualizadas no seguinte diagrama:

image

[1] "An Economical Engine for the Purpose of Pumping Water by the Expansive Force of Steam" (Um motor econ mico para bombear gua pela for a expansiva do vapor), Robert Stirling, Patente Brit nica No. 4081 de 1816.

No primeiro est gio o número de moles ($n$) o g s comprimido com o trabalho realizado no sistema ($W_{in}$) de o volume expandido ($V_1$) a o volume compactado ($V_2$) isotermicamente a la temperatura no estado 1 ($T_1$) com o número de moles ($n$) e la pressão ($p$), integrada em o volume ($V$), de o volume expandido ($V_1$) a o volume compactado ($V_2$):

equation=10253

Se la pressão ($p$) for obtido usando la constante de gás universal ($R_C$), o número de moles ($n$) e la temperatura absoluta ($T$) com a equa o dos gases

equation=3183

a integral para la temperatura absoluta ($T$) igual a la temperatura no estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Portanto,

equation=15365

No segundo est gio adicionado o calor fornecido ($Q_H$) que, dependendo de la capacidade térmica em volume constante ($C_V$), aumenta a temperatura de la temperatura no estado 1 ($T_1$) para la temperatura no estado 2 ($T_2$):

image

Ao fornecer o calor fornecido ($Q_H$), a temperatura do g s aumenta de $T_2$ para $T_3$ em um processo isoc rico ( volume constante). Isso implica que podemos utilizar a rela o para ERROR:8085 com la capacidade térmica em volume constante ($C_V$) e ERROR:7510, expressa pela equa o:

equation=4862

Isso resulta nos valores de la temperatura no estado 2 ($T_2$) e la temperatura no estado 3 ($T_3$) da seguinte forma:

equation=15363

No terceiro est gio o número de moles ($n$) o g s se expande formando o trabalho realizado pelo sistema ($W_{out}$) enquanto o volume se expande de o volume compactado ($V_2$) para o volume expandido ($V_1$) isotermicamente para <. var>8490:

image

O trabalho calculado usando a integral de o trabalho realizado pelo sistema ($W_{out}$) com la pressão ($p$), integrada em o volume ($V$), de o volume expandido ($V_1$) a o volume compactado ($V_2$):

equation=10253

Se la pressão ($p$) obtido usando la constante de gás universal ($R_C$), o número de moles ($n$), e la temperatura absoluta ($T$) com a equa o dos gases

equation=3183

a integral para la temperatura absoluta ($T$) igual a la temperatura no estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Portanto,

equation=15366

No quarto est gio, o calor absorvido ($Q_C$) reduzido, o que, dependendo de la capacidade térmica em volume constante ($C_V$), diminui a temperatura de la temperatura no estado 2 ($T_2$) para la temperatura no estado 1 ($T_1$) :

kyon

Ao remover o calor absorvido ($Q_C$) quando o volume ($V$) igual a ERROR:8498,0, la temperatura absoluta ($T$) aumenta de la temperatura no estado 1 ($T_1$) para la temperatura no estado 2 ($T_2$). Isso implica que podemos utilizar a rela o para ERROR:8085 com la capacidade térmica em volume constante ($C_V$) e ERROR:7510, que expressa pela equa o:

equation=4862

isso nos leva express o:

equation=15364

La eficiência ($\eta$) definido como a propor o de o trabalho eficaz ($W$) para o o calor contribuiu para o sistema ($Q$):

equation=15756

onde o trabalho eficaz ($W$) est relacionado a o trabalho realizado pelo sistema ($W_{out}$) e o trabalho realizado no sistema ($W_{in}$) atrav s de:

equation=15758

enquanto o o calor contribuiu para o sistema ($Q$) est associado a o calor fornecido ($Q_H$), que definido como:

equation=15757

Considerando que o trabalho realizado pelo sistema ($W_{out}$) est relacionado a o número de moles ($n$), la temperatura no estado 2 ($T_2$), o volume expandido ($V_1$), o volume compactado ($V_2$) e la constante de gás universal ($R_C$) por meio de:

equation=15366

e o trabalho realizado no sistema ($W_{in}$) est associado a la temperatura no estado 1 ($T_1$) atrav s de:

equation=15365

e o calor fornecido ($Q_H$) est vinculado a la capacidade térmica em volume constante ($C_V$) por:

equation=15363

la eficiência ($\eta$) pode ser calculado, resultando em:

equation=15759

model

O calor fornecido ($Q_H$) a ser adicionado depende de la capacidade térmica em volume constante ($C_V$) e da diferen a de temperatura de la temperatura no estado 1 ($T_1$) a la temperatura no estado 2 ($T_2$):

kyon

O trabalho realizado pelo sistema ($W_{out}$) est com o número de moles ($n$), la constante de gás universal ($R_C$), la temperatura no estado 2 ($T_2$), o volume expandido ($V_1$) e o volume compactado ($V_2$) igual:

kyon

O calor absorvido ($Q_C$) a ser adicionado depende de la capacidade térmica em volume constante ($C_V$) e da diferen a de temperatura de la temperatura no estado 2 ($T_2$) para la temperatura no estado 1 ($T_1$):

kyon

O trabalho realizado no sistema ($W_{in}$) est com o número de moles ($n$), la constante de gás universal ($R_C$), la temperatura no estado 1 ($T_1$), o volume expandido ($V_1$) e o volume compactado ($V_2$) igual:

kyon

O trabalho eficaz ($W$) compreende o trabalho realizado no sistema ($W_{in}$) e o trabalho realizado pelo sistema ($W_{out}$):

kyon.

O o calor contribuiu para o sistema ($Q$) compreende o calor fornecido ($Q_H$) e o trabalho realizado no sistema ($W_{in}$):

kyon.

La eficiência ($\eta$) pode ser definido como a porcentagem que o trabalho eficaz ($W$) representa em o o calor contribuiu para o sistema ($Q$):

kyon.

La eficiência ($\eta$) do ciclo Stirling depende de la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), o volume expandido ($V_1$), o volume compactado ($V_2$), la capacidade térmica em volume constante ($C_V$), o número de moles ($n$) e la constante de gás universal ($R_C$):

kyon.