O ciclo consiste em quatro processos revers veis: dois isot rmicos (temperatura constante) e dois adiab ticos (sem troca de calor). Durante a expans o isot rmica, o sistema (geralmente um g s) absorve calor de um reservat rio de alta temperatura, expandindo-se e realizando trabalho sobre o ambiente. Isso seguido por uma expans o adiab tica, onde o sistema continua a realizar trabalho, mas sem trocar calor, resultando em seu resfriamento. O g s ent o passa por uma compress o isot rmica, liberando calor para um reservat rio mais frio enquanto trabalho realizado no g s para comprimi-lo. O ciclo termina com uma compress o adiab tica, que eleva ainda mais a temperatura do g s, retornando-o ao seu estado original.

A beleza do ciclo de Carnot reside na sua simplicidade e na vis o que oferece sobre os limites de efici ncia para todos os motores baseados em calor. A efici ncia de um motor de Carnot depende apenas das temperaturas dos reservat rios quente e frio e independente da subst ncia de trabalho ou dos detalhes do processo em si. Essa efici ncia expressa como a rela o entre a diferen a de temperatura entre os reservat rios e a temperatura mais alta, mostrando que nenhum motor real operando entre dois reservat rios de calor pode ser mais eficiente que um motor de Carnot operando entre os mesmos reservat rios.

mechanisms

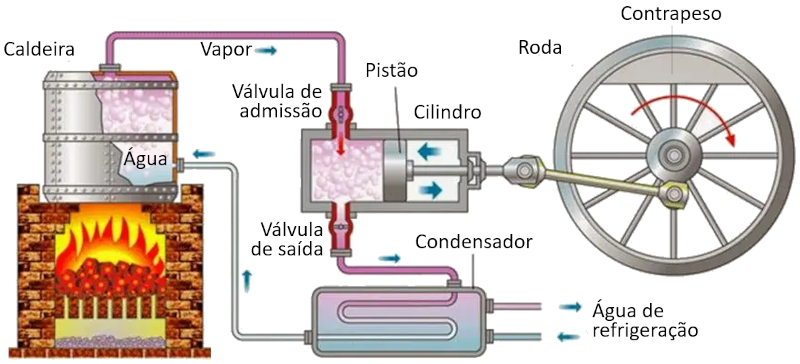
Em uma m quina que utiliza o conceito de Carnot, ocorrem os seguintes processos:

• O reservat rio com a temperatura mais alta criado usando um forno.
• O reservat rio com a temperatura mais baixa criado usando um sistema de refrigera o.
• O vapor gerado a partir do reservat rio se expande em forma de g s, deslocando o pist o e elevando a massa de compensa o. Na primeira etapa isoterma, a primeira v lvula est aberta enquanto a segunda est fechada. Na segunda etapa do processo, a primeira v lvula fechada e a expans o continua adiabaticamente.
• Na terceira etapa, a segunda v lvula aberta e, com a ajuda da massa de compensa o, o pist o retorna e o g s expelido de forma isoterma. Na quarta etapa, a v lvula fechada e o processo conclu do adiabaticamente.

image

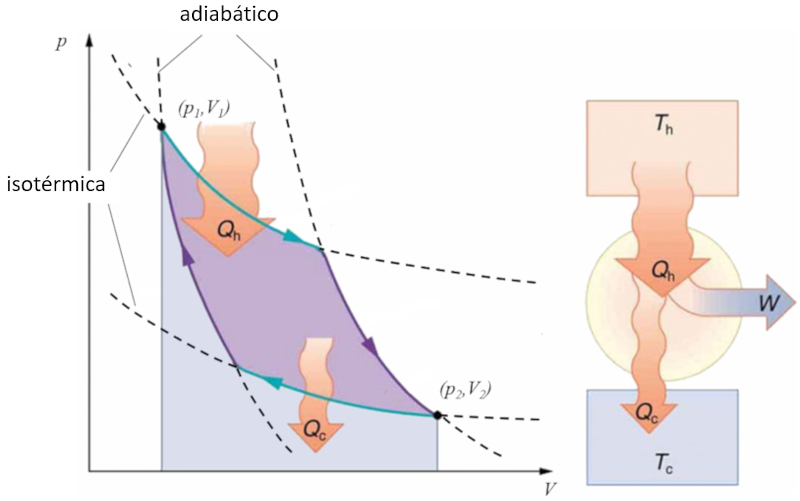
Sadi Carnot introduziu [1] o conceito te rico do primeiro projeto de m quina capaz de gerar trabalho mec nico com base em um gradiente de temperatura. Isso alcan ado por meio de um processo no espa o press o-volume, onde calor adicionado e extra do, conforme ilustrado na imagem:

image

A rea sob a curva o calor fornecido ($Q_H$), que se estende de 1 a 2, representa a energia necess ria para transitar do estado ($p_1, V_1$) para o estado ($p_2, V_2$). Por outro lado, a rea sob a curva o calor absorvido ($Q_C$), indo de 2 para 1, representa a extra o de energia necess ria para retornar do estado ($p_2, V_2$) ao estado ($p_1, V_1$). A diferen a entre essas reas corresponde regi o delimitada por ambas as curvas e representa o trabalho eficaz ($W$) que o sistema pode realizar.

Carnot tamb m demonstrou que, de acordo com a segunda lei da termodin mica, o calor fornecido ($Q_H$) n o pode ser igual a zero. Isso implica que n o existem m quinas capazes de converter todo o calor em trabalho.

[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflex es sobre a Pot ncia Motriz do Fogo e sobre M quinas Adequadas para Desenvolver Essa Pot ncia), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)

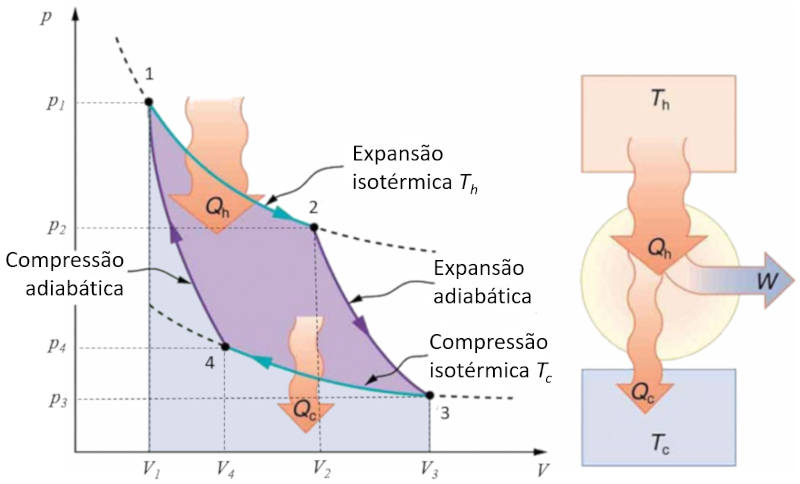
O ciclo de Carnot descrito de forma simples como um ciclo no qual o trabalho realizado alternadamente de maneira isot rmica e adiab tica. Em particular, s o estudados os diagramas press o-volume e temperatura-entropia. No primeiro caso, as quatro etapas que ocorrem podem ser identificadas da seguinte forma:

Etapa 1 para 2: Expans o isot rmica.
Etapa 2 para 3: Expans o adiab tica.
Etapa 3 para 4: Compress o isot rmica.
Etapa 4 para 1: Compress o adiab tica.
Essas etapas s o representadas abaixo:

image

No diagrama anexado, ilustrado o fluxo de energia, onde o calor fornecido ($Q_H$) (quente) sai do reservat rio em la alta temperatura ($T_H$), entra no sistema, realiza trabalho $W$, enquanto o complemento ERROR:8171,0 (frio) absorvido pelo reservat rio em la temperatura baixa ($T_C$).

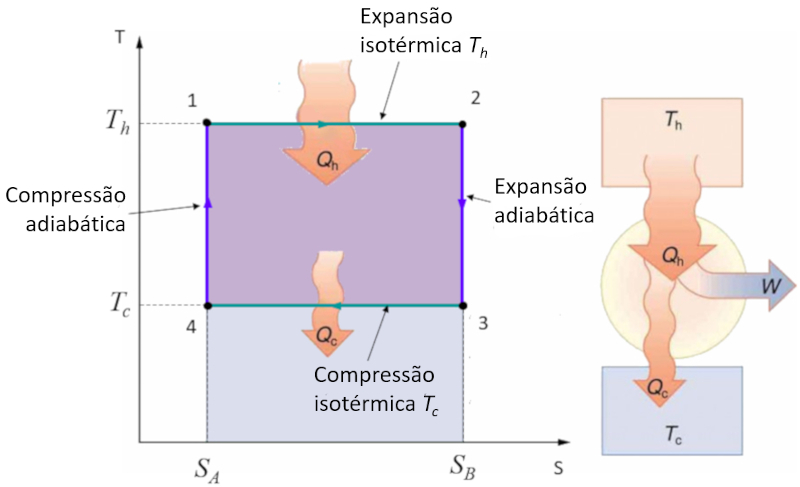
O ciclo de Carnot descrito de forma simples como um ciclo em que se trabalha alternadamente de forma isot rmica e adiab tica. Em particular, s o estudados os diagramas de press o-volume e temperatura-entropia. No caso do diagrama temperatura-entropia, o diagrama simplificado ao passar de est gios isot rmicos para est gios de entropia constante:

No diagrama temperatura-entropia, os est gios de entropia constante s o representados da seguinte forma:

image

Nessas etapas, la entropia ($S$) permanece constante, o que implica que n o h transfer ncia de calor, enquanto la temperatura absoluta ($T$) pode variar. Isso simplifica a representa o do ciclo e permite uma an lise mais direta das propriedades termodin micas do sistema.

Uma vez que o diferencial de trabalho impreciso ($\delta W$) definido em termos de la pressão ($p$) e la variação de volume ($\Delta V$) da seguinte forma:

equation=3468

Podemos calcular o trabalho eficaz ($W$) integrando ao longo das curvas do diagrama do ciclo:

$W = \displaystyle\oint pdV$

Usando a primeira lei da termodin mica com o diferencial de energia interna ($dU$) e o diferencial de calor impreciso ($\delta Q$):

equation=9632

E considerando o percurso no diagrama de la temperatura absoluta ($T$) e la entropia ($S$), obtemos com la variação de entropia ($dS$):

$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$

Uma vez que a integral ao longo de um caminho fechado de um diferencial exato igual a zero, temos:

equation=11139

Visto que la eficiência ($\eta$) com o trabalho eficaz ($W$) e o calor fornecido ($Q_H$)

equation=11154

ele pode ser substitu do por o trabalho eficaz ($W$), o que, junto com o calor fornecido ($Q_H$) e o calor absorvido ($Q_C$), resulta em

equation=11135

produzindo a seguinte rela o:

equation=11155

La eficiência ($\eta$) uma fun o de o calor fornecido ($Q_H$) e o calor absorvido ($Q_C$), dada por:

equation=11155

Podemos expressar o calor fornecido ($Q_H$) em termos de la temperatura baixa ($T_C$), la baixa entropia ($S_C$) e la alta entropia ($S_H$) como:

equation=11138

E usando la alta temperatura ($T_H$) como:

equation=11137

Se substituirmos essas express es, obtemos:

equation=11136

model

Se, no ciclo de Carnot, o calor fornecido ($Q_H$) retirado do reservat rio de temperatura mais alta e o calor absorvido ($Q_C$) entregue ao reservat rio de temperatura mais baixa, gerado um trabalho eficaz ($W$), que igual a:

kyon

O calor absorvido ($Q_C$) igual a la temperatura baixa ($T_C$) devido diferen a na entropia, ou seja, la alta entropia ($S_H$) e la baixa entropia ($S_C$):

kyon

O calor fornecido ($Q_H$) igual a la alta temperatura ($T_H$) devido diferen a de entropia, ou seja, la alta entropia ($S_H$) e la baixa entropia ($S_C$):

kyon

La eficiência ($\eta$) pode ser definido como a porcentagem que o trabalho eficaz ($W$) representa em rela o a o calor fornecido ($Q_H$):

kyon.

La eficiência ($\eta$) pode ser calculado a partir de o calor fornecido ($Q_H$) e o calor absorvido ($Q_C$) como

kyon

La eficiência ($\eta$) pode ser calculado com base em la alta temperatura ($T_H$) e la temperatura baixa ($T_C$) com:

kyon