Usuario:


Flujo de un líquido incompresible
Storyboard

Cuando un líquido se mueve, hablamos de flujo, y su medida se basa en el volumen que atraviesa una sección en un período de tiempo determinado. Si asumimos que el volumen se desplaza sin deformarse, la velocidad a la que el líquido pasa a través de la sección será constante. En este contexto, el flujo también se puede definir como el producto de la velocidad y la sección transversal.

>Modelo

ID:(875, 0)


Mecanismos
Concepto


ID:(15485, 0)


Flujo de volumen
Concepto

Durante un tiempo transcurrido ($\Delta t$), el fluido con una velocidad media del fluido ($v$) se desplaza un elemento del tubo ($\Delta s$). Si la sección ($S$) representa la cantidad de fluido que atraviesa dicha sección en el tiempo transcurrido ($\Delta t$), se calcula mediante:

$\Delta V = S \Delta s = Sv \Delta t$



Esta ecuación determina que el volumen de fluido que fluye a través de la sección la sección ($S$) durante un tiempo transcurrido ($\Delta t$) es igual al producto del área de la sección y la distancia que el fluido recorre en ese tiempo.



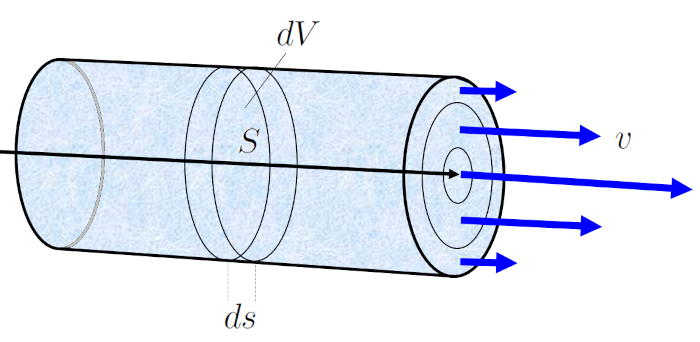
Esto facilita el cálculo de el elemento de volumen ($\Delta V$), que es el volumen de fluido que fluye por el canal en un período específico de el tiempo transcurrido ($\Delta t$), correspondiente a el flujo de volumen ($J_V$).

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

ID:(2212, 0)


Flujo de volumen y su velocidad
Concepto

El flujo se define como el volumen el elemento de volumen ($\Delta V$) dividido por el tiempo el tiempo transcurrido ($\Delta t$), lo cual se expresa en la siguiente ecuación:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



y el volumen es el producto de la sección la sección del tubo ($S$) por el desplazamiento el elemento del tubo ($\Delta s$):

$ \Delta V = S \Delta s $



Dado que el desplazamiento el elemento del tubo ($\Delta s$) dividido por el tiempo el tiempo transcurrido ($\Delta t$) equivale a la velocidad, se representa con:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Por lo tanto, el flujo es una densidad de flujo ($j_s$), que se calcula mediante:

$ j_s = \displaystyle\frac{ J_V }{ S }$



Es crucial destacar que en este modelo:

La densidad de flujo actúa como una velocidad promedio a través de toda la sección del flujo.

ID:(15715, 0)


Canal de sección variable
Concepto

Considerando un tubo que no filtra ni recibe adiciones de líquido, el flujo que entra en un punto 1 El flujo de volumen 1 ($J_{V1}$) será igual al flujo que sale en un punto 2 El flujo de volumen 2 ($J_{V2}$):

$ J_{V1} = J_{V2} $



Dentro de un canal o tubo, es posible que ocurra un cambio en la sección transversal, ya sea que se amplíe o reduzca.



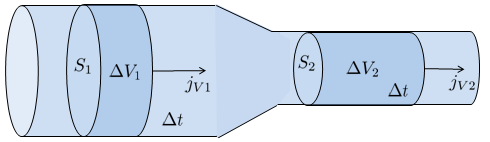
Esta variación impactará directamente en el flujo a través de la densidad de flujo ($j_s$), que representa la velocidad, aumentando (si se reduce la sección) o disminuyendo (si se amplía) de acuerdo con la sección del tubo ($S$) para mantener el flujo de volumen ($J_V$) constante, como lo indica la ecuación:

$ j_s = \displaystyle\frac{ J_V }{ S }$



La conservación del flujo, junto con la definición de densidad de flujo, resulta en la ley de conservación de modo que la sección en el punto 1 ($S_1$), la sección en el punto 2 ($S_2$), la densidad de flujo 1 ($j_{s1}$) y la densidad de flujo 2 ($j_{s2}$) cumplen:

$ S_1 j_{s1} = S_2 j_{s2} $

ID:(2213, 0)


Validez de la Ecuación de Continuidad
Concepto

La ecuación de continuidad es una herramienta fundamental para el análisis de los flujos de fluidos en tuberías y canales. Sin embargo, su aplicación requiere que el flujo sea estable y uniforme, sin la presencia de flujos en la dirección opuesta o turbulencias, que pueden afectar la precisión de los cálculos. Por lo tanto, es importante verificar que el flujo en el conducto sea realmente laminar y no presente turbulencias.Existen varias formas de detectar turbulencias en el flujo, como el uso de medidores de flujo o la observación visual del flujo. En cualquier caso, es esencial asegurarse de que el flujo sea estable antes de aplicar la ecuación de continuidad, ya que cualquier perturbación en el flujo puede alterar la precisión de los cálculos y afectar la eficiencia del sistema en general.

ID:(978, 0)


Modelo
Concepto


ID:(15488, 0)


Flujo de un líquido incompresible
Modelo

Cuando un líquido se mueve, hablamos de flujo, y su medida se basa en el volumen que atraviesa una sección en un período de tiempo determinado. Si asumimos que el volumen se desplaza sin deformarse, la velocidad a la que el líquido pasa a través de la sección será constante. En este contexto, el flujo también se puede definir como el producto de la velocidad y la sección transversal.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$j_{s1}$
j_s1
Densidad de flujo 1
m/s
$j_{s2}$
j_s2
Densidad de flujo 2
m/s
$J_{V1}$
J_V1
Flujo de volumen 1
m^3/s
$J_{V2}$
J_V2
Flujo de volumen 2
m^3/s
$\Delta s_1$
Ds_1
Largo del elemento 1
m
$\Delta s_2$
Ds_2
Largo del elemento 2
m
$r_1$
r_1
Radio de la sección 1
m
$r_2$
r_2
Radio de la sección 2
m
$S_1$
S_1
Sección en el punto 1
m^2
$S_2$
S_2
Sección en el punto 2
m^2
$\Delta t$
Dt
Tiempo transcurrido
s
$\Delta V_1$
DV_1
Volumen del elemento 1
m^3
$\Delta V_2$
DV_2
Volumen del elemento 2
m^3

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

El flujo se define como el volumen el elemento de volumen ($\Delta V$) dividido por el tiempo el tiempo transcurrido ($\Delta t$), lo cual se expresa en la siguiente ecuaci n:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



y el volumen es el producto de la secci n la sección del tubo ($S$) por el desplazamiento el elemento del tubo ($\Delta s$):

$ \Delta V = S \Delta s $



Dado que el desplazamiento el elemento del tubo ($\Delta s$) dividido por el tiempo el tiempo transcurrido ($\Delta t$) equivale a la velocidad, se representa con:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Por lo tanto, el flujo es una densidad de flujo ($j_s$), que se calcula mediante:

$ j_s = \displaystyle\frac{ J_V }{ S }$

(ID 4349)

El flujo se define como el volumen el elemento de volumen ($\Delta V$) dividido por el tiempo el tiempo transcurrido ($\Delta t$), lo cual se expresa en la siguiente ecuaci n:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



y el volumen es el producto de la secci n la sección del tubo ($S$) por el desplazamiento el elemento del tubo ($\Delta s$):

$ \Delta V = S \Delta s $



Dado que el desplazamiento el elemento del tubo ($\Delta s$) dividido por el tiempo el tiempo transcurrido ($\Delta t$) equivale a la velocidad, se representa con:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Por lo tanto, el flujo es una densidad de flujo ($j_s$), que se calcula mediante:

$ j_s = \displaystyle\frac{ J_V }{ S }$

(ID 4349)

La continuidad implica que el flujo de volumen 1 ($J_{V1}$) y el flujo de volumen 2 ($J_{V2}$) son iguales

$ J_{V1} = J_{V2} $



lleva a que la densidad de flujo 1 ($j_{s1}$) por la sección en el punto 1 ($S_1$)

$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$



y a que la densidad de flujo 2 ($j_{s2}$) por la velocidad máxima en el flujo por un cilindro ($v_{max}$)

$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$



se obtiene que

$ S_1 j_{s1} = S_2 j_{s2} $

(ID 4350)

Ejemplos


(ID 15485)

Durante un tiempo transcurrido ($\Delta t$), el fluido con una velocidad media del fluido ($v$) se desplaza un elemento del tubo ($\Delta s$). Si la sección ($S$) representa la cantidad de fluido que atraviesa dicha secci n en el tiempo transcurrido ($\Delta t$), se calcula mediante:

$\Delta V = S \Delta s = Sv \Delta t$



Esta ecuaci n determina que el volumen de fluido que fluye a trav s de la secci n la sección ($S$) durante un tiempo transcurrido ($\Delta t$) es igual al producto del rea de la secci n y la distancia que el fluido recorre en ese tiempo.



Esto facilita el c lculo de el elemento de volumen ($\Delta V$), que es el volumen de fluido que fluye por el canal en un per odo espec fico de el tiempo transcurrido ($\Delta t$), correspondiente a el flujo de volumen ($J_V$).

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

(ID 2212)

El flujo se define como el volumen el elemento de volumen ($\Delta V$) dividido por el tiempo el tiempo transcurrido ($\Delta t$), lo cual se expresa en la siguiente ecuaci n:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



y el volumen es el producto de la secci n la sección del tubo ($S$) por el desplazamiento el elemento del tubo ($\Delta s$):

$ \Delta V = S \Delta s $



Dado que el desplazamiento el elemento del tubo ($\Delta s$) dividido por el tiempo el tiempo transcurrido ($\Delta t$) equivale a la velocidad, se representa con:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Por lo tanto, el flujo es una densidad de flujo ($j_s$), que se calcula mediante:

$ j_s = \displaystyle\frac{ J_V }{ S }$



Es crucial destacar que en este modelo:

La densidad de flujo act a como una velocidad promedio a trav s de toda la secci n del flujo.

(ID 15715)

Considerando un tubo que no filtra ni recibe adiciones de l quido, el flujo que entra en un punto 1 El flujo de volumen 1 ($J_{V1}$) ser igual al flujo que sale en un punto 2 El flujo de volumen 2 ($J_{V2}$):

$ J_{V1} = J_{V2} $



Dentro de un canal o tubo, es posible que ocurra un cambio en la secci n transversal, ya sea que se ampl e o reduzca.



Esta variaci n impactar directamente en el flujo a trav s de la densidad de flujo ($j_s$), que representa la velocidad, aumentando (si se reduce la secci n) o disminuyendo (si se ampl a) de acuerdo con la sección del tubo ($S$) para mantener el flujo de volumen ($J_V$) constante, como lo indica la ecuaci n:

$ j_s = \displaystyle\frac{ J_V }{ S }$



La conservaci n del flujo, junto con la definici n de densidad de flujo, resulta en la ley de conservaci n de modo que la sección en el punto 1 ($S_1$), la sección en el punto 2 ($S_2$), la densidad de flujo 1 ($j_{s1}$) y la densidad de flujo 2 ($j_{s2}$) cumplen:

$ S_1 j_{s1} = S_2 j_{s2} $

(ID 2213)

La ecuaci n de continuidad es una herramienta fundamental para el an lisis de los flujos de fluidos en tuber as y canales. Sin embargo, su aplicaci n requiere que el flujo sea estable y uniforme, sin la presencia de flujos en la direcci n opuesta o turbulencias, que pueden afectar la precisi n de los c lculos. Por lo tanto, es importante verificar que el flujo en el conducto sea realmente laminar y no presente turbulencias.Existen varias formas de detectar turbulencias en el flujo, como el uso de medidores de flujo o la observaci n visual del flujo. En cualquier caso, es esencial asegurarse de que el flujo sea estable antes de aplicar la ecuaci n de continuidad, ya que cualquier perturbaci n en el flujo puede alterar la precisi n de los c lculos y afectar la eficiencia del sistema en general.

(ID 978)


(ID 15488)

ID:(875, 0)