Particle exchange
Storyboard 
The exchange of substances between the atmosphere and the ocean can include particles. This is particularly relevant when studying the transfer of CO2 molecules from the atmosphere to the ocean.Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014Chapter: Transfer Across the Air-Sea Interface
ID:(1630, 0)
CO2 diffusion
Description 
The absorption of CO2 by the oceans helps mitigate the effects of this gas in the atmosphere and therefore delays climate change. However, the processes involved are more complex and include:
- Gas exchange with the atmosphere: The ocean and the atmosphere are in constant exchange of CO2 through gas diffusion. Atmospheric CO2 dissolves in the surface of the ocean and forms carbonic acid (H2CO3), which then dissociates into hydrogen ions (H+) and bicarbonate ions (HCO3-). This process helps balance the CO2 levels between the ocean and the atmosphere.
- Photosynthesis and respiration: Marine organisms, such as phytoplankton and algae, perform photosynthesis and take up CO2 from the water to produce organic matter and release oxygen. This process, known as carbon fixation, helps extract CO2 from the ocean. On the other hand, marine organisms also respire, which means they release CO2 into the water during the decomposition of organic matter.
- Ocean circulation: The ocean is characterized by its global circulation, in which currents transport CO2-rich water from the surface to the depths and vice versa. This contributes to the distribution and mixing of CO2 throughout the ocean, allowing deep waters to store large amounts of dissolved CO2.
- Sedimentation and burial: Part of the organic matter produced by marine organisms, including CO2 captured through photosynthesis, can sink to the ocean floor. As sediments accumulate over geological time, the organic carbon can become buried and stored in the seafloor for long periods.
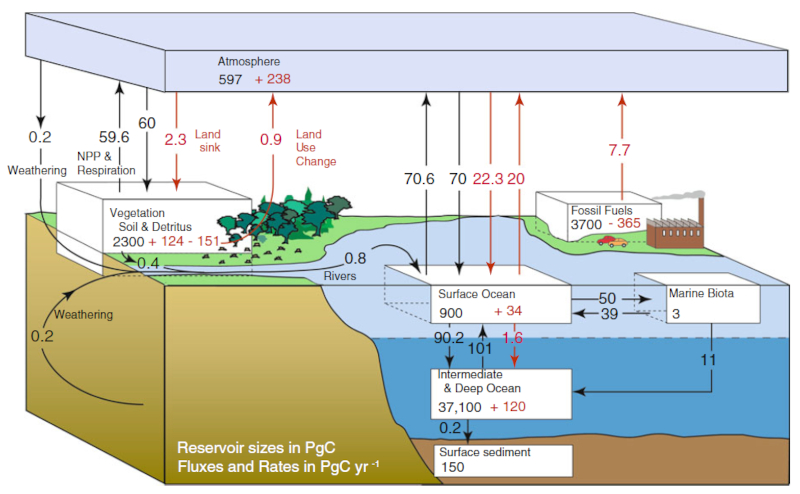
Annual carbon flux in PgC/yr. Numbers in black are pre-industrial revolution, in red are increases related to the industrial revolution. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss Martin T. Johnson (Editors), Springer, 2014
Depending on the area and time of the planet, there is a greater concentration of carbon in the atmosphere than in the ocean or vice versa, thus defining whether the flow of carbon is from air to water or vice versa.
ID:(12297, 0)
Transfer rate and relative speed
Description 
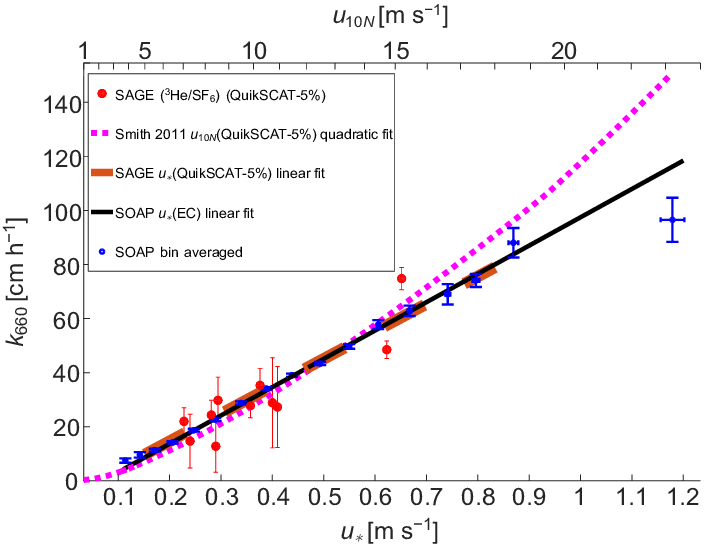
In a first approximation, the dependence of the gas transfer rate in water ($k_w$) in relation to the relative velocity, calculated by subtracting the velocidad del agua ($u_w$) from the velocidad del aire ($u_a$), is proportional to
$k_w \propto u_a - u_w$
as observed in the graph:
ID:(12298, 0)
Transfer rate and Schmidt number
Description 
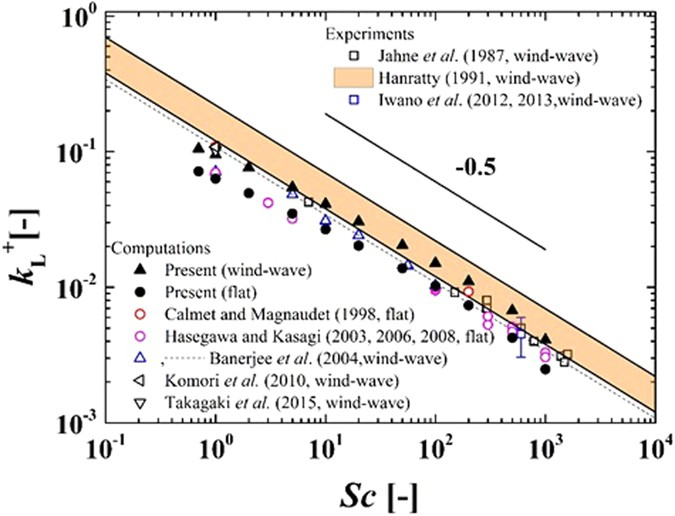
The relationship between the gas transfer rate in water ($k_w$) is inversely proportional to the schmidt number ($Sc$), so it is expressed as proportional to that number raised to ERROR:9926, which is negative:
$k_w\propto Sc^n$
which is represented with ERROR:9926 equal to -0.5:
ID:(12299, 0)
Solubility as a function of Schmidt number
Concept 
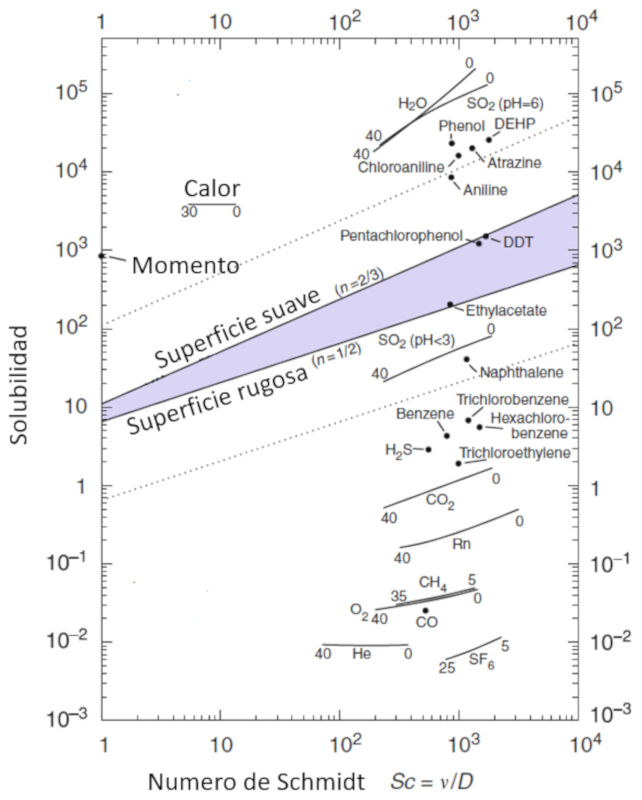
The mobility of molecules, represented by the gas solubility ($\alpha$), is modeled as a function of particle concentration, characterized by the schmidt number ($Sc$), which in turn is calculated from parameters the viscosidad en masa acuosa ($\eta$), the densidad en capa de masa acuosa ($\rho$), and the constante de difusión en masa acuosa ($D$) using the following expression:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
This relationship is visualized in the following diagram:
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12245, 0)
CO2 exchange, speed from water
Concept 
The gas transfer rate in water ($k_w$) can be modeled using measured data. Firstly, it depends on the rate at which the system removes carbon from the air-water interface, making the transport speed proportional to the relative velocity between the two mediums.
Secondly, there is an effect of ion mobility, which can be described by the schmidt number ($Sc$), representing the relationship between momentum diffusion and particles. However, this dependence is not linear and is influenced by a factor ERROR:9926 that varies between -1/2 and -2/3 depending on the surface roughness.
Finally, the gas transfer rate in water ($k_w$) also depends on the factor beta del transporte aire a agua de CO2 ($\beta$), which in turn is determined by the level of surface roughness.
In summary, the gas the gas transfer rate in water ($k_w$) is described as a function of the velocidad del agua ($u_w$), the velocidad del aire ($u_a$), the schmidt number ($Sc$), the factor beta del transporte aire a agua de CO2 ($\beta$), and ERROR:9926 as follows:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Particle exchange
Model 
The exchange of substances between the atmosphere and the ocean can include particles. This is particularly relevant when studying the transfer of CO2 molecules from the atmosphere to the ocean. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014 Chapter: Transfer Across the Air-Sea Interface
Variables
Calculations
Calculations
Equations
If we consider the gas flux as $F$ and the transport velocity as $k$, according to the general relationship:
| $ \Delta C = C_{w,0} - C_{a,0} $ |
By replacing the concentration difference $C_0 - C_b$ with the difference in partial pressure of the gas using the solubility $\alpha$, we have:
$C_0 - C_b = \alpha \Delta p_{CO2}$
we can obtain:
| $ F_w = k_w \Delta C $ |
(ID 12214)
In the Monin-Obukhov Similarity Theory (MOST) model, the flux of elements such as gases is estimated by considering the difference in concentrations between the air and water, represented by
$C_z - C_0$
and the flux is calculated using the transfer coefficient $D_C$ and the surface velocity $U_z$, as follows:
| $ F_z = D_C U_z ( C_z - C_{a,0} )$ |
This allows for the estimation of the flux of elements between the air and water.
(ID 12224)
The diffusive flux $F$ is described by Fick\'s law:
| $ F = - D \displaystyle\frac{d C }{d t }$ |
where $D$ is the diffusion constant and $dC/dx$ is the concentration gradient. By defining a transfer velocity as:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
we can establish a flow equation of the form:
| $ F_a =- k_a \Delta C $ |
(ID 12226)
Examples
(ID 15636)
The absorption of CO2 by the oceans helps mitigate the effects of this gas in the atmosphere and therefore delays climate change. However, the processes involved are more complex and include:
- Gas exchange with the atmosphere: The ocean and the atmosphere are in constant exchange of CO2 through gas diffusion. Atmospheric CO2 dissolves in the surface of the ocean and forms carbonic acid (H2CO3), which then dissociates into hydrogen ions (H+) and bicarbonate ions (HCO3-). This process helps balance the CO2 levels between the ocean and the atmosphere.
- Photosynthesis and respiration: Marine organisms, such as phytoplankton and algae, perform photosynthesis and take up CO2 from the water to produce organic matter and release oxygen. This process, known as carbon fixation, helps extract CO2 from the ocean. On the other hand, marine organisms also respire, which means they release CO2 into the water during the decomposition of organic matter.
- Ocean circulation: The ocean is characterized by its global circulation, in which currents transport CO2-rich water from the surface to the depths and vice versa. This contributes to the distribution and mixing of CO2 throughout the ocean, allowing deep waters to store large amounts of dissolved CO2.
- Sedimentation and burial: Part of the organic matter produced by marine organisms, including CO2 captured through photosynthesis, can sink to the ocean floor. As sediments accumulate over geological time, the organic carbon can become buried and stored in the seafloor for long periods.

Annual carbon flux in PgC/yr. Numbers in black are pre-industrial revolution, in red are increases related to the industrial revolution. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss Martin T. Johnson (Editors), Springer, 2014
Depending on the area and time of the planet, there is a greater concentration of carbon in the atmosphere than in the ocean or vice versa, thus defining whether the flow of carbon is from air to water or vice versa.
(ID 12297)
In a first approximation, the dependence of the gas transfer rate in water ($k_w$) in relation to the relative velocity, calculated by subtracting the velocidad del agua ($u_w$) from the velocidad del aire ($u_a$), is proportional to
$k_w \propto u_a - u_w$
as observed in the graph:

(ID 12298)
The relationship between the gas transfer rate in water ($k_w$) is inversely proportional to the schmidt number ($Sc$), so it is expressed as proportional to that number raised to ERROR:9926, which is negative:
$k_w\propto Sc^n$
which is represented with ERROR:9926 equal to -0.5:

(ID 12299)
The mobility of molecules, represented by the gas solubility ($\alpha$), is modeled as a function of particle concentration, characterized by the schmidt number ($Sc$), which in turn is calculated from parameters the viscosidad en masa acuosa ($\eta$), the densidad en capa de masa acuosa ($\rho$), and the constante de difusión en masa acuosa ($D$) using the following expression:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
This relationship is visualized in the following diagram:

Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
(ID 12245)
The gas transfer rate in water ($k_w$) can be modeled using measured data. Firstly, it depends on the rate at which the system removes carbon from the air-water interface, making the transport speed proportional to the relative velocity between the two mediums.
Secondly, there is an effect of ion mobility, which can be described by the schmidt number ($Sc$), representing the relationship between momentum diffusion and particles. However, this dependence is not linear and is influenced by a factor ERROR:9926 that varies between -1/2 and -2/3 depending on the surface roughness.
Finally, the gas transfer rate in water ($k_w$) also depends on the factor beta del transporte aire a agua de CO2 ($\beta$), which in turn is determined by the level of surface roughness.
In summary, the gas the gas transfer rate in water ($k_w$) is described as a function of the velocidad del agua ($u_w$), the velocidad del aire ($u_a$), the schmidt number ($Sc$), the factor beta del transporte aire a agua de CO2 ($\beta$), and ERROR:9926 as follows:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
(ID 15652)
(ID 15641)
ID:(1630, 0)
