Estabilidad Vertical
Storyboard 
La estabilidad de la columna del agua marina depende tanto de la temperatura como de la salinidad de esta.Si la temperatura aumenta, el agua se expande generando una zona de menor densidad, tendiendo a que el volumen trate de flotar.Si, por el contrario, aumenta la salinidad, la densidad aumenta, con lo que el volumen tiende a hundirse.En ese sentido, existe una competencia entre los efectos de la temperatura y la salinidad en que el volumen puede tratar de emerger o hundirse. El último caso es clave para la generación de corrientes de profundidad.
ID:(1524, 0)
Estabilidad de la columna de agua
Descripción 
Normalmente, la densidad del agua marina aumenta con la profundidad.
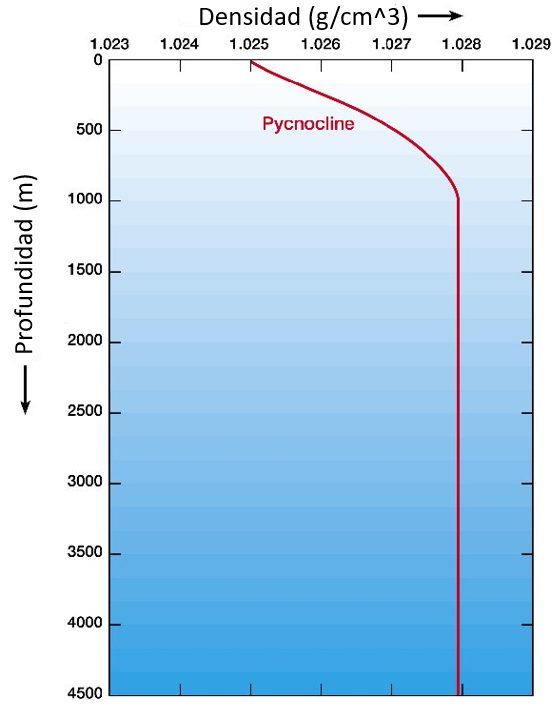
Esto significa que las capas más cercanas a la superficie son más ligeras que las capas más profundas. Esto garantiza que estas capas floten sobre las capas más profundas y no tiendan a desplazarlas.
Sin embargo, las fluctuaciones en la temperatura y salinidad pueden hacer que las capas más profundas tengan una densidad menor que las capas superiores. Esto crea una situación inestable, ya que estas capas tienden a flotar y emerger sobre las capas superiores.
Solo en situaciones en las que la densidad es constante o aumenta con la profundidad el sistema es estable.
Por otro lado, cuando un sistema se vuelve inestable, significa que ante una perturbación puede colapsar, pero si no se perturba, puede mantener su estado actual.
ID:(12045, 0)
Variación de temperatura y salinidad
Concepto 
El aumento de la variación de la temperatura ($\Delta T$) provoca una dilatación térmica que hace que la variación de volumen por temperatura ($\Delta V_T$) aumente en relación a el volumen ($V$) con el coeficiente de dilatación térmica ($k_T$), como se muestra en:
| $ k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T }$ |
De manera similar, el aumento de la variación de la salinidad ($\Delta s$) debido a la masa ocasiona que ERROR:8624 aumente en relación a la densidad del agua marína ($\rho$) con el coeficiente de salinidad ($k_s$), como se muestra en:
| $ k_s =\displaystyle\frac{ 1 }{ \rho }\displaystyle\frac{ \Delta\rho }{ \Delta s }$ |
Esta expresión es equivalente a la expresión en la que la variación de volumen por salinidad ($\Delta V_s$) disminuye (valor negativo), como se muestra en:
| $ k_s \equiv - \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_s }{ \Delta s }$ |
Por lo tanto, el papel de la temperatura y la salinidad es fundamental, ya que pueden hacer que la columna de agua oceánica se vuelva inestable, haciendo que un elemento de volumen comience a flotar o hundirse, invirtiendo así la columna.
ID:(15514, 0)
Inestabilidad en el agua en caso de diferencia de temperatura
Descripción 
Cuando se calienta agua en una olla, se forma una zona de menor densidad en el fondo, cerca de la fuente de calor. Esta zona comienza a elevarse buscando desplazar la capa superior, que al ser más fría, es más densa y tiende a hundirse.
Una vez que la diferencia de temperatura entre la superficie y el fondo supera un valor crítico, comienzan a formarse chorros de agua caliente que llegan a la superficie y crean espacio para que el agua superficial descienda hacia el fondo:
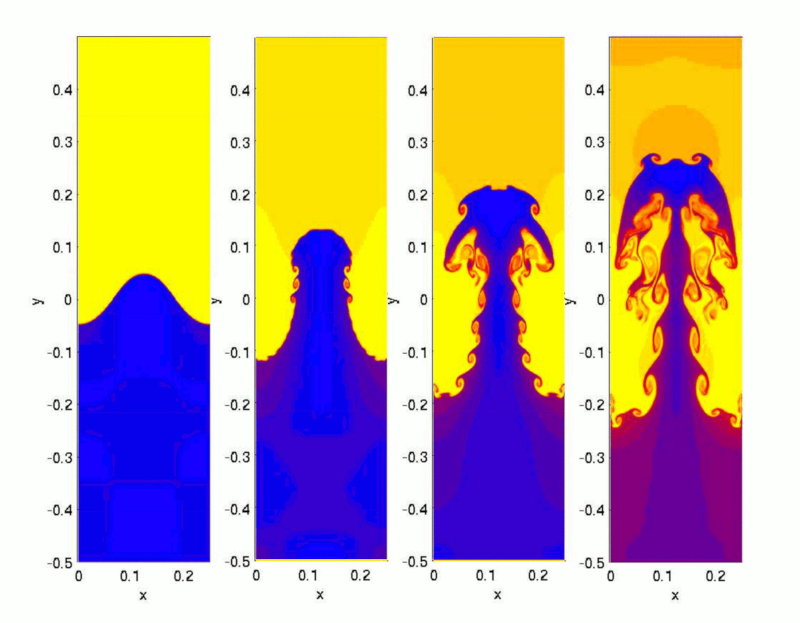
ID:(12046, 0)
Estabilidad de la columna de agua marina
Imagen 
En el caso del agua marina, no solo puede haber variaciones en la temperatura, sino también variaciones en la salinidad. La salinidad generalmente aumenta la densidad, por lo que los procesos que reducen la salinidad en la profundidad pueden llevar a inestabilidades.
En este escenario, se forman zonas donde el agua con mayor salinidad desciende mientras que el agua con menor concentración asciende. Estas zonas de hundimiento de sal se conocen como dedos de sal y se pueden observar en el siguiente gráfico generado a través de simulación:
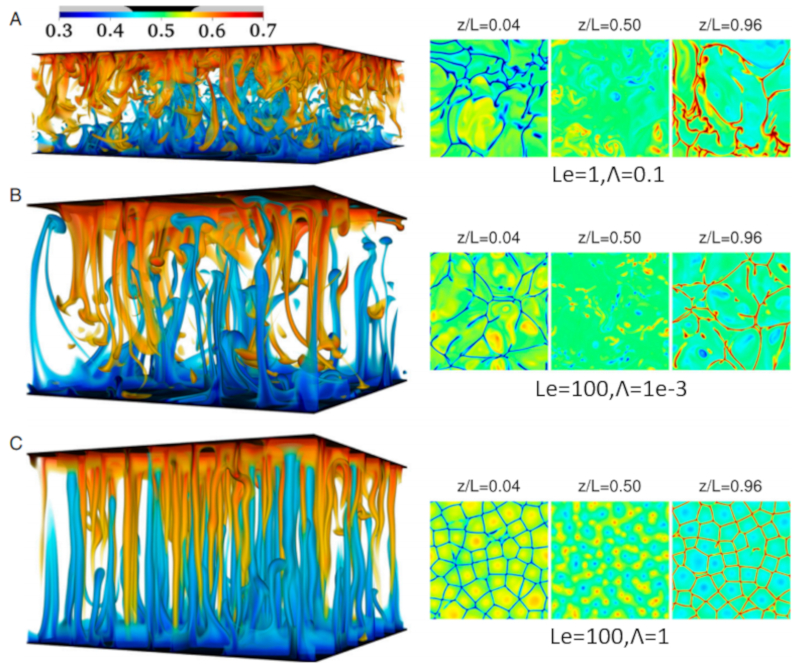
ID:(12051, 0)
Concepto de difusión
Descripción 
La difusión corresponde a un movimiento aleatorio de las moléculas que se distribuyen gradualmente en el espacio. Los múltiples choques hacen que las moléculas inviertan frecuentemente su dirección de movimiento, lo que resulta en una expansión muy lenta. Para describir este movimiento, se utilizan conceptos estadísticos, como describir la zona donde se encuentran la mayoría de las partículas mediante la desviación estándar. De hecho, esta desviación estándar crece linealmente en el tiempo:

La constante de proporcionalidad se denomina constante de difusión.Este concepto también se utiliza para describir cómo se propagan las propiedades de las partículas, como el momento y la energía, dentro de un sistema. En este caso, no se modifica la distribución espacial de las partículas, sino la distribución espacial del parámetro considerado.
ID:(13405, 0)
Número de Rayleigh para temperatura y estabilidad
Concepto 
Cuando se calienta agua en una olla, el agua cerca del fondo comienza a calentarse, lo que provoca su expansión en una variación de volumen por temperatura ($\Delta V_T$) según la relación de dilatación térmica en la que cumple con el coeficiente de dilatación térmica ($k_T$), el volumen ($V$) y la variación de la temperatura ($\Delta T$) mediante:
| $ k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T }$ |
la fuerza de flotación ($F_b$) es proporcional al volumen desplazado y se puede expresar aproximadamente como:
$F_b \sim g \Delta V \sim k_T V \Delta T$
Al analizar las unidades, podemos observar que el factor
$\Delta V g \rightarrow \displaystyle\frac{m^4}{s^2}$
es el cuadrado de una constante de difusión. Por lo tanto, la inestabilidad se puede entender como la dominancia de la constante de difusión del momento ($D_p$) de convección en comparación con la constante de difusión térmica ($D_T$) necesaria para aumentar la temperatura y la pérdida de momento debido a la viscosidad.
Por lo tanto, si la siguiente proporción:
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
es mucho mayor que la unidad, la convección dominará. En este sentido, tiene sentido definir un número adimensional característico conocido como el número de Rayleigh para temperatura ($Ra_T$):
| $ Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T$ |
En el caso de un sistema sin bordes, se ha demostrado que el límite crítico para la inestabilidad ocurre cuando el número de Rayleigh supera $Ra_L=657.51$. Sin embargo, este límite depende de la geometría del sistema, y en el caso de un cilindro (como una olla sin tapa), se ha demostrado que es inestable cuando $Ra_L=1,100.65$.
ID:(15510, 0)
Factor lambda
Concepto 
La tendencia de que un elemento de agua oceánica flote debido al aumento de temperatura o se hunda debido al aumento de salinidad se representa en el siguiente diagrama:
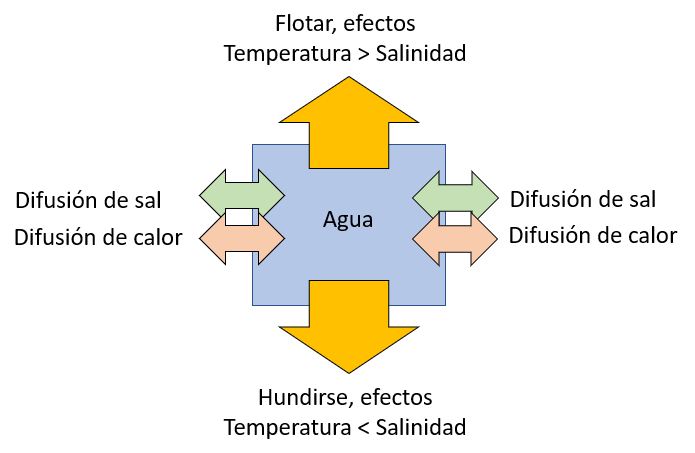
Para estudiar la situación, introducimos el factor lambda ($\Lambda$) como la proporción de el número de Rayleigh para temperatura ($Ra_T$) y el numero de Rayleigh para la salinidad ($Ra_s$):
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s} = \displaystyle\frac{k_T \Delta T}{k_s \Delta s}$
Dado que el número de Rayleigh para temperatura ($Ra_T$) depende de la aceleración gravitacional ($g$), el coeficiente de dilatación térmica ($k_T$), la variación de la temperatura ($\Delta T$), la constante de difusión del momento ($D_p$) y la constante de difusión térmica ($D_T$) según la ecuación:
| $ Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T$ |
y el numero de Rayleigh para la salinidad ($Ra_s$) depende de el coeficiente de salinidad ($k_s$), la variación de la salinidad ($\Delta s$) y la constante de difusión de partículas ($D_N$) según la ecuación:
| $ Ra_s \equiv\displaystyle\frac{ g k_s h ^3 }{ D_p D_N } \Delta s $ |
obtenemos la relación para el factor lambda ($\Lambda$) mediante:
| $ \Lambda \equiv \displaystyle\frac{ k_T \Delta T }{ k_s \Delta s }$ |
ID:(15511, 0)
Número de Lewis
Concepto 
El numero de Lewis ($Le$) compara la constante de difusión térmica ($D_T$), que depende de la conducción termica del oceano ($\lambda_T$), el calor específico ($c$) y la densidad del agua marína ($\rho$), según:
| $ D_T \equiv \displaystyle\frac{ \lambda_T }{ \rho c }$ |
con la constante de difusión de partículas ($D_N$), que depende de la movilidad de partículas ($\mu$), la constante de Boltzmann ($k_B$) y la temperatura absoluta ($T$), según:
| $ D_N \equiv \mu k_B T $ |
Por lo tanto, se define como:
| $ Le \equiv \displaystyle\frac{ D_T }{ D_N }$ |
ID:(15512, 0)
Condición de estabilidad
Concepto 
Para mantener el sistema estable, es necesario que la difusión de energía (temperatura) y salinidad no logren generar una la fuerza de flotación ($F_b$) lo suficientemente grande como para invertir la columna. Esto se logra cuando el factor lambda ($\Lambda$) es mayor que el numero de Lewis ($Le$).
Por lo tanto, el sistema es estable si se cumple la siguiente condición:
| $ Le < \Lambda $ |
Es importante tener en cuenta que el factor de número depende de la temperatura y la salinidad, por lo que si estas variables varían, es posible que el sistema alcance un punto de inestabilidad.
ID:(15515, 0)
Estabilidad Vertical
Modelo 
La estabilidad de la columna del agua marina depende tanto de la temperatura como de la salinidad de esta. Si la temperatura aumenta, el agua se expande generando una zona de menor densidad, tendiendo a que el volumen trate de flotar. Si, por el contrario, aumenta la salinidad, la densidad aumenta, con lo que el volumen tiende a hundirse. En ese sentido, existe una competencia entre los efectos de la temperatura y la salinidad en que el volumen puede tratar de emerger o hundirse. El último caso es clave para la generación de corrientes de profundidad.
Variables
Cálculos
Cálculos
Ecuaciones
Dado que el número de Rayleigh para temperatura ($Ra_T$) depende de la aceleración gravitacional ($g$), la profundidad ($h$), la variación de la temperatura ($\Delta T$), la constante de difusión del momento ($D_p$) e la constante de difusión térmica ($D_T$), como se define en:
| $ Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T$ |
y el numero de Rayleigh para la salinidad ($Ra_s$) depende de el coeficiente de salinidad ($k_s$) y la variación de la salinidad ($\Delta s$), conforme definido por:
| $ Ra_s \equiv\displaystyle\frac{ g k_s h ^3 }{ D_p D_N } \Delta s $ |
ent o, podemos afirmar que
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s}$
se reduz a:
| $ \Lambda \equiv \displaystyle\frac{ k_T \Delta T }{ k_s \Delta s }$ |
(ID 12056)
(ID 12057)
Como la densidad del agua marína ($\rho$) es igual a una masa $m$ dividida por el volumen ($V$), expresada como:
$\rho =\displaystyle\frac{m}{V}$
Si diferenciamos esta expresi n para una masa $m$ constante, resulta en un ERROR:8624 como:
$\Delta\rho =-\displaystyle\frac{m}{V^2}\Delta V=-\displaystyle\frac{\rho}{V}\Delta V$
Por lo tanto, la expresi n en el coeficiente de salinidad ($k_s$) con la variación de la salinidad ($\Delta s$):
| $ k_s =\displaystyle\frac{ 1 }{ \rho }\displaystyle\frac{ \Delta\rho }{ \Delta s }$ |
implica:
| $ k_s \equiv - \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_s }{ \Delta s }$ |
(ID 15513)
Ejemplos
(ID 15508)
Normalmente, la densidad del agua marina aumenta con la profundidad.

Esto significa que las capas m s cercanas a la superficie son m s ligeras que las capas m s profundas. Esto garantiza que estas capas floten sobre las capas m s profundas y no tiendan a desplazarlas.
Sin embargo, las fluctuaciones en la temperatura y salinidad pueden hacer que las capas m s profundas tengan una densidad menor que las capas superiores. Esto crea una situaci n inestable, ya que estas capas tienden a flotar y emerger sobre las capas superiores.
Solo en situaciones en las que la densidad es constante o aumenta con la profundidad el sistema es estable.
Por otro lado, cuando un sistema se vuelve inestable, significa que ante una perturbaci n puede colapsar, pero si no se perturba, puede mantener su estado actual.
(ID 12045)
El aumento de la variación de la temperatura ($\Delta T$) provoca una dilataci n t rmica que hace que la variación de volumen por temperatura ($\Delta V_T$) aumente en relaci n a el volumen ($V$) con el coeficiente de dilatación térmica ($k_T$), como se muestra en:
| $ k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T }$ |
De manera similar, el aumento de la variación de la salinidad ($\Delta s$) debido a la masa ocasiona que ERROR:8624 aumente en relaci n a la densidad del agua marína ($\rho$) con el coeficiente de salinidad ($k_s$), como se muestra en:
| $ k_s =\displaystyle\frac{ 1 }{ \rho }\displaystyle\frac{ \Delta\rho }{ \Delta s }$ |
Esta expresi n es equivalente a la expresi n en la que la variación de volumen por salinidad ($\Delta V_s$) disminuye (valor negativo), como se muestra en:
| $ k_s \equiv - \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_s }{ \Delta s }$ |
Por lo tanto, el papel de la temperatura y la salinidad es fundamental, ya que pueden hacer que la columna de agua oce nica se vuelva inestable, haciendo que un elemento de volumen comience a flotar o hundirse, invirtiendo as la columna.
(ID 15514)
Cuando se calienta agua en una olla, se forma una zona de menor densidad en el fondo, cerca de la fuente de calor. Esta zona comienza a elevarse buscando desplazar la capa superior, que al ser m s fr a, es m s densa y tiende a hundirse.
Una vez que la diferencia de temperatura entre la superficie y el fondo supera un valor cr tico, comienzan a formarse chorros de agua caliente que llegan a la superficie y crean espacio para que el agua superficial descienda hacia el fondo:

(ID 12046)
En el caso del agua marina, no solo puede haber variaciones en la temperatura, sino tambi n variaciones en la salinidad. La salinidad generalmente aumenta la densidad, por lo que los procesos que reducen la salinidad en la profundidad pueden llevar a inestabilidades.
En este escenario, se forman zonas donde el agua con mayor salinidad desciende mientras que el agua con menor concentraci n asciende. Estas zonas de hundimiento de sal se conocen como dedos de sal y se pueden observar en el siguiente gr fico generado a trav s de simulaci n:

(ID 12051)
La difusi n corresponde a un movimiento aleatorio de las mol culas que se distribuyen gradualmente en el espacio. Los m ltiples choques hacen que las mol culas inviertan frecuentemente su direcci n de movimiento, lo que resulta en una expansi n muy lenta. Para describir este movimiento, se utilizan conceptos estad sticos, como describir la zona donde se encuentran la mayor a de las part culas mediante la desviaci n est ndar. De hecho, esta desviaci n est ndar crece linealmente en el tiempo:

La constante de proporcionalidad se denomina constante de difusi n.Este concepto tambi n se utiliza para describir c mo se propagan las propiedades de las part culas, como el momento y la energ a, dentro de un sistema. En este caso, no se modifica la distribuci n espacial de las part culas, sino la distribuci n espacial del par metro considerado.
(ID 13405)
Cuando se calienta agua en una olla, el agua cerca del fondo comienza a calentarse, lo que provoca su expansi n en una variación de volumen por temperatura ($\Delta V_T$) seg n la relaci n de dilataci n t rmica en la que cumple con el coeficiente de dilatación térmica ($k_T$), el volumen ($V$) y la variación de la temperatura ($\Delta T$) mediante:
| $ k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T }$ |
la fuerza de flotación ($F_b$) es proporcional al volumen desplazado y se puede expresar aproximadamente como:
$F_b \sim g \Delta V \sim k_T V \Delta T$
Al analizar las unidades, podemos observar que el factor
$\Delta V g \rightarrow \displaystyle\frac{m^4}{s^2}$
es el cuadrado de una constante de difusi n. Por lo tanto, la inestabilidad se puede entender como la dominancia de la constante de difusión del momento ($D_p$) de convecci n en comparaci n con la constante de difusión térmica ($D_T$) necesaria para aumentar la temperatura y la p rdida de momento debido a la viscosidad.
Por lo tanto, si la siguiente proporci n:
$\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T$
es mucho mayor que la unidad, la convecci n dominar . En este sentido, tiene sentido definir un n mero adimensional caracter stico conocido como el número de Rayleigh para temperatura ($Ra_T$):
| $ Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T$ |
En el caso de un sistema sin bordes, se ha demostrado que el l mite cr tico para la inestabilidad ocurre cuando el n mero de Rayleigh supera $Ra_L=657.51$. Sin embargo, este l mite depende de la geometr a del sistema, y en el caso de un cilindro (como una olla sin tapa), se ha demostrado que es inestable cuando $Ra_L=1,100.65$.
(ID 15510)
La tendencia de que un elemento de agua oce nica flote debido al aumento de temperatura o se hunda debido al aumento de salinidad se representa en el siguiente diagrama:

Para estudiar la situaci n, introducimos el factor lambda ($\Lambda$) como la proporci n de el número de Rayleigh para temperatura ($Ra_T$) y el numero de Rayleigh para la salinidad ($Ra_s$):
$\Lambda = \displaystyle\frac{Ra_T}{Ra_s} = \displaystyle\frac{k_T \Delta T}{k_s \Delta s}$
Dado que el número de Rayleigh para temperatura ($Ra_T$) depende de la aceleración gravitacional ($g$), el coeficiente de dilatación térmica ($k_T$), la variación de la temperatura ($\Delta T$), la constante de difusión del momento ($D_p$) y la constante de difusión térmica ($D_T$) seg n la ecuaci n:
| $ Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T$ |
y el numero de Rayleigh para la salinidad ($Ra_s$) depende de el coeficiente de salinidad ($k_s$), la variación de la salinidad ($\Delta s$) y la constante de difusión de partículas ($D_N$) seg n la ecuaci n:
| $ Ra_s \equiv\displaystyle\frac{ g k_s h ^3 }{ D_p D_N } \Delta s $ |
obtenemos la relaci n para el factor lambda ($\Lambda$) mediante:
| $ \Lambda \equiv \displaystyle\frac{ k_T \Delta T }{ k_s \Delta s }$ |
(ID 15511)
El numero de Lewis ($Le$) compara la constante de difusión térmica ($D_T$), que depende de la conducción termica del oceano ($\lambda_T$), el calor específico ($c$) y la densidad del agua marína ($\rho$), seg n:
| $ D_T \equiv \displaystyle\frac{ \lambda_T }{ \rho c }$ |
con la constante de difusión de partículas ($D_N$), que depende de la movilidad de partículas ($\mu$), la constante de Boltzmann ($k_B$) y la temperatura absoluta ($T$), seg n:
| $ D_N \equiv \mu k_B T $ |
Por lo tanto, se define como:
| $ Le \equiv \displaystyle\frac{ D_T }{ D_N }$ |
(ID 15512)
Para mantener el sistema estable, es necesario que la difusi n de energ a (temperatura) y salinidad no logren generar una la fuerza de flotación ($F_b$) lo suficientemente grande como para invertir la columna. Esto se logra cuando el factor lambda ($\Lambda$) es mayor que el numero de Lewis ($Le$).
Por lo tanto, el sistema es estable si se cumple la siguiente condici n:
| $ Le < \Lambda $ |
Es importante tener en cuenta que el factor de n mero depende de la temperatura y la salinidad, por lo que si estas variables var an, es posible que el sistema alcance un punto de inestabilidad.
(ID 15515)
(ID 15509)
ID:(1524, 0)
