Druyd:Knowledge

Modelos con Vectores

Storyboard

>Model

ID:(350, 0)

Malaria case

Definition

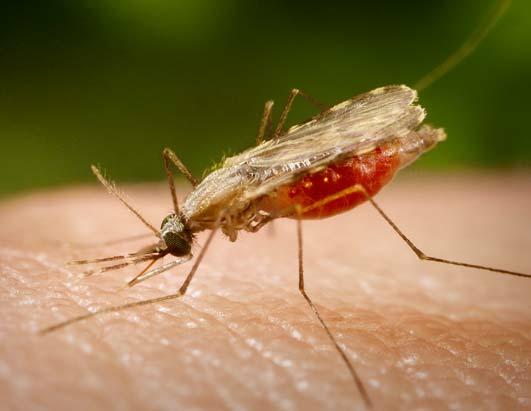
In the case of malaria, it is necessary to model not only the infection but also the evolution of the carrier.

In the case of malaria it is a parasite that is transmitted by mosquitoes. In the process the mosquito females transmit the parasite to the human being and vice versa the infected human being can infect the mosquito.

2.7 million people die annually from this disease.

ID:(877, 0)

Vectors Models

Image

ID:(874, 0)

Mosquito

Note

ID:(3023, 0)

Modelos con Vectores

Description

Variables

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

$I_{crit}$

I_crit

Asymptotic Infected

$V_{\infty}$

V_t

Asymptotic Vectors

$\mu$

Death of Mosquito Factor

$\Lambda$

Fraction Females Mosquitos

$N_I$

N_I

Human Population

$I_t$

I_t

Infected

$dI$

Infected Variation

$dt$

Infinitesimal Variation of Time

$N_V$

N_V

Mosquito Population

$p_b$

p_b

Probability of being Bite by Time

1/s

$p_I$

p_I

Probability of Infecting bite Human Being

$p_V$

p_V

Probability of Infecting the Mosquito Bite

$R_0$

R_0

Propagation Factor

$\gamma$

gamma

Recovery Time Factor

1/s

$V$

Vector

$dV$

Vector Variation

Calculations

Equation

Number

First, select the equation:

, then, select the variable:

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable

Given

Calculate

Target :

Equation

To be used

Equations

$\displaystyle\frac{dI}{dt}=p_bp_I\Lambda\displaystyle\frac{V}{N_V}(N_I-I)-\gamma I$

\displaystyle\frac{dI}{dt}=p_bp_I\Lambda\displaystyle\frac{V}{N_V}(N_I-I)-\gamma I

(ID 4094)

$\displaystyle\frac{dV}{dt}=p_bp_V\displaystyle\frac{I}{N_I}(N_V-V)-\mu V$

\displaystyle\frac{dV}{dt}=p_bp_V\displaystyle\frac{I}{N_I}(N_V-V)-\mu V

(ID 4095)

$I_{\infty}=N_I\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{p_bp_V(\gamma+\Lambda p_bp_I)}$

I_{\infty}=N_I(Lambda p_b^2p_Ip_V-mu gamma)/(p_bp_V(gamma+Lambda p_bp_I))

(ID 4096)

$V_{\infty}=N_V\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{\Lambda p_bp_I(\mu+p_bp_V)}$

V_infty=N_V(Lambda p_b^2p_Ip_V-mu gamma)/(Lambda p_bp_I(mu+p_bp_V))

(ID 4097)

$R_0=\displaystyle\frac{p_b^2p_Vp_I\Lambda}{\mu\gamma}$

R_0=p_b^2p_Vp_I Lambda/(mu gamma)

(ID 4098)

$ i =\displaystyle\frac{ I }{ N_I }$

i = I / N_I

(ID 8204)

$ v =\displaystyle\frac{ V }{ N_V }$

v = V / N_V

(ID 8205)

$\displaystyle\frac{dv}{dt}=p_bp_Vi(1-v)-\mu v$

dv / dt = p_b * p_V * i *(1- v )- \mu * v

(ID 8206)

$\displaystyle\frac{di}{dt}=p_bp_I\Lambda v(1-i)-\gamma i$

di/dt=p_bp_I\Lambda v(1-i)-\gamma i

(ID 8207)

$i_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{p_bp_V(\gamma+\Lambda p_bp_I)}$

i_infty=(Lambda p_b^2p_Ip_V-mu gamma)/(p_bp_V(gamma+Lambda p_bp_I))

(ID 8209)

$v_{\infty}=\displaystyle\frac{\Lambda p_b^2p_Ip_V-\mu\gamma}{\Lambda p_bp_I(\mu+p_bp_V)}$

v_infty=(Lambda p_b^2p_Ip_V-mu gamma)/(Lambda p_bp_I(mu+p_bp_V))

(ID 8210)

Examples

Malaria case

In the case of malaria, it is necessary to model not only the infection but also the evolution of the carrier.

2.7 million people die annually from this disease.

(ID 877)

Vectors Models

(ID 874)

Mosquito

(ID 3023)

Vector model simulation

With the equation for the fraction of infected humans

$\displaystyle\frac{di}{dt}=p_bp_I\Lambda v(1-i)-\gamma i$

and the fraction of infected mosquitoes is

$\displaystyle\frac{dv}{dt}=p_bp_Vi(1-v)-\mu v$

You can run a simulation that shows the dynamics of both populations.

(ID 8208)

ID:(350, 0)