Zellularen Automaten
Bild 
Die zellularen Automaten sind Modelle, die die Raumzeit diskretisieren und Automaten in jedem Punkt (Zelle) des Netzwerks definieren, die in der Funktion dessen arbeiten, was ihre Nachbarn tun (Automaten, weil sie eine definierte Form der Reaktion haben). Ein Beispiel ist eine sechseckige Struktur:
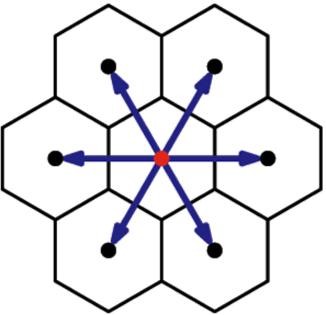
Modell D2Q7 (zwei Dimensionen und 7 Elemente pro Zelle - 6 Seiten und 1 Mitte)
Im Fall, dass es auf ein teilchenförmiges Gas angewendet wird, kann jeder Knoten (Zustände 0 und 1) ein Teilchen enthalten, das nur Geschwindigkeiten mit den Richtungen haben kann, die zwischen den Zellen verknüpfen.
In der Simulation mit Modellen wie zellularen Automaten gibt es zwei Phasen:
- Zelle wirkt auf die anderen
- Zelle verarbeitet Aktionen der Umwelt
Im speziellen Fall der Modellierung eines Gases entspricht der erste Schritt dem Fliessen (Streaming), während der zweite zur Kollision (Kollision).
Die mathematische Beschreibung erfolgt durch die Partikelverteilungsfunktion
| $f_i(\vec{x},t)=w_if(\vec{x},\vec{v}_i,t)$ |
ID:(8494, 0)
D2Q9 Modelle (zweidimensionale, 9 Punkte)
Notiz 
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n
$\vec{e}_0=(0,0)$
\\n\\nen las esquinas\\n\\n
$\vec{e}_1=(1,0)$
(E),\\n
$\vec{e}_2=(0,1)$
(N), \\n
$\vec{e}_3=(-1,0)$
(W) y \\n
$\vec{e}_4=(0,-1)$
(S)\\n\\ny en las diagonales\\n\\n
$\vec{e}_5=(1,1)$
(NE), \\n
$\vec{e}_6=(-1,1)$
(SE), \\n
$\vec{e}_7=(-1,-1)$
(SW) y \\n
$\vec{e}_8=(1,-1)$
(NW)
lo que se representa en la siguiente gráfica:
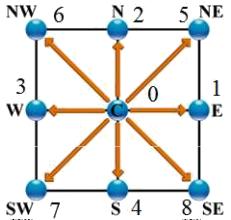
ID:(8496, 0)
D3Q15 Modelle (dreidimensionale, 15 Punkte)
Zitat 
Das D3Q15 Modell ist ein zweidimensionales Modell (D3), in dem der Knoten (Punkt center) Knoten entlang der kartesischen Achsen verbindet\\n\\n
$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) (0,0,-1)$
\\n\\nund in den Ecken des Würfels\\n\\n
$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$
was es in der folgenden Grafik dargestellt ist:
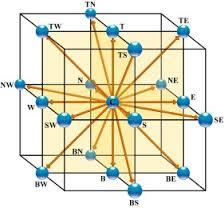
Es ist relativ einfach Modelle zu bauen vom Typ D3Q19 (einschließlich der Hälften der Seitenkanten ) oder D3Q27 (alle möglichen Punkte).
ID:(8497, 0)
Discretization und Zellstruktur im LBM Ansatz
Storyboard 
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
F r Diskretisierung in LBM arbeitet nicht Modelle mit Funktionen der Geschwindigkeit, wenn nicht mit diskreten Komponenten. So ist die Komponente
wobei
Die Dispersion wird mit dem zugeordneten Relaxationszeit mit
Bei der Diskretisiert wir davon ausgehen, dass die Partikel mit einer durchschnittlichen Geschwindigkeit
verbunden ist.
Die zellularen Automaten sind Modelle, die die Raumzeit diskretisieren und Automaten in jedem Punkt (Zelle) des Netzwerks definieren, die in der Funktion dessen arbeiten, was ihre Nachbarn tun (Automaten, weil sie eine definierte Form der Reaktion haben). Ein Beispiel ist eine sechseckige Struktur:
Modell D2Q7 (zwei Dimensionen und 7 Elemente pro Zelle - 6 Seiten und 1 Mitte)
Im Fall, dass es auf ein teilchenf rmiges Gas angewendet wird, kann jeder Knoten (Zust nde 0 und 1) ein Teilchen enthalten, das nur Geschwindigkeiten mit den Richtungen haben kann, die zwischen den Zellen verkn pfen.
In der Simulation mit Modellen wie zellularen Automaten gibt es zwei Phasen:
- Zelle wirkt auf die anderen
- Zelle verarbeitet Aktionen der Umwelt
Im speziellen Fall der Modellierung eines Gases entspricht der erste Schritt dem Fliessen (Streaming), w hrend der zweite zur Kollision (Kollision).
Die mathematische Beschreibung erfolgt durch die Partikelverteilungsfunktion
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n
$\vec{e}_0=(0,0)$
\\n\\nen las esquinas\\n\\n
$\vec{e}_1=(1,0)$
(E),\\n
$\vec{e}_2=(0,1)$
(N), \\n
$\vec{e}_3=(-1,0)$
(W) y \\n
$\vec{e}_4=(0,-1)$
(S)\\n\\ny en las diagonales\\n\\n
$\vec{e}_5=(1,1)$
(NE), \\n
$\vec{e}_6=(-1,1)$
(SE), \\n
$\vec{e}_7=(-1,-1)$
(SW) y \\n
$\vec{e}_8=(1,-1)$
(NW)
lo que se representa en la siguiente gr fica:
Das D3Q15 Modell ist ein zweidimensionales Modell (D3), in dem der Knoten (Punkt center) Knoten entlang der kartesischen Achsen verbindet\\n\\n
$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) (0,0,-1)$
\\n\\nund in den Ecken des W rfels\\n\\n
$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$
was es in der folgenden Grafik dargestellt ist:
Es ist relativ einfach Modelle zu bauen vom Typ D3Q19 (einschlie lich der H lften der Seitenkanten ) oder D3Q27 (alle m glichen Punkte).
ID:(1135, 0)
