Wenn die Wand eine Neigung haben bez glich des Netzwerk es in einer komplexere Modellierung notwendig:

image

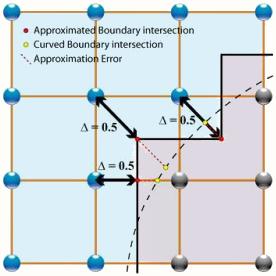
Allgemeine Umrandung

Zun chst muss eine ungef hre Grenze festgelegt werden um dann die entsprechende Gleichungen definiert werden. Diese wird dann innerhalb des Streamng Prozess angewandt.

Wenn der R ckprall nicht an einem Punkt des Netzes sondern in einem Abstand \Delta eintritt:

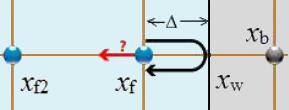
image\\n\\ndann sollte die Funktion die Beitr ge der Abweichungen ber cksichtigen\\n\\n

$f_i(x_f,t+\delta t)=\displaystyle\frac{(1-\Delta)f_{-i}(x_f,t)+\Delta(f_{-i}(x_b,t)+f_{-i}(x_{f2},t)}{1+\Delta}$

In Streaming Prozess werden die Partikel entlang ihrer Geschwindigkeitsrichtungen von benachbarten Zellen bewegen

equation

wobei \vec{x} die Position, t Zeit, \vec{e}_i die Richtung des Rasters und c ist die Geschwindigkeit.

Im Falle eines D2Q9 Systems sind die 9 Werte f_i als O, N, E, S, W, NE, SE, SW, NW benannt werden. Wenn die Anzahl der Partikel in der Position (n,m) als f_i(j,k) bezeichnet werden, dann sind die Gleichungen

```

N[x,y] = N[x,y-1]

NW[x,y] = NW[x+1,y-1]

E[x,y] = E[x-1,y]

NE[x,y] = NE[x-1,y-1]

S[x,y] = S[x,y+1]

SE[x,y] = SE[x-1,y+1]

W[x,y] = W[x+1,y]

SW[x,y] = SW[x+1,y+1]

```