User:


Review of the Lattice Boltzmann Method (LBM)
Storyboard

The Lattice Boltzmann Method (LBM) was created to reduce the processing time in the solution of hydro and aerodynamic problems. Instead of solving the Navier Stokes differential equation, it uses an equivalent representation based on the Boltzmann transport equation and reduces the processing effort by working with a simplified discrete phase space. The result is a high-speed simulator capable of describing highly complex processes.

>Model

ID:(1162, 0)


Boltzmann equation
Equation

>Top, >Model


The Boltzmann function describes the transport of a particle system described by the velocity distribution function:

$\displaystyle\frac{\partial f}{\partial t}+v_i\displaystyle\frac{\partial f}{\partial x_i}=C(f)$

Where the term C describes the interaction (collisions) between them.

ID:(8462, 0)


Density
Equation

>Top, >Model


If the parameters are calculated by averaging over the speed using

$ \chi_k(\vec{x},t) =\displaystyle\frac{1}{c(\vec{x},t)}\displaystyle\int d\vec{v} f(\vec{x},\vec{v},t) \chi_k(\vec{x},\vec{v},t)$



the mass density estimation is obtained by:

$\rho(\vec{x},t) = m\displaystyle\int f(\vec{x},\vec{v},t)d\vec{v}$

ID:(8458, 0)


Speed of the Flow
Equation

>Top, >Model


If the parameters are calculated by averaging over the speed using

$ \chi_k(\vec{x},t) =\displaystyle\frac{1}{c(\vec{x},t)}\displaystyle\int d\vec{v} f(\vec{x},\vec{v},t) \chi_k(\vec{x},\vec{v},t)$



the velocity of the flow is calculated by integrating the velocity distribution function on all velocities by weighing the velocities:

$\vec{u}(\vec{x},t) = \displaystyle\frac{m}{\rho}\int \vec{v}f(\vec{x},\vec{v},t)d\vec{v}$

ID:(8459, 0)


Temperature
Equation

>Top, >Model


If the parameters are calculated by averaging over the speed using

$ \chi_k(\vec{x},t) =\displaystyle\frac{1}{c(\vec{x},t)}\displaystyle\int d\vec{v} f(\vec{x},\vec{v},t) \chi_k(\vec{x},\vec{v},t)$



and the equipartition theorem is considered, the temperature can be estimated by integrating the kinetic energy weighted by the velocity distribution divided by the gas constant:

$T(\vec{x},t) = \displaystyle\frac{m}{3R\rho}\displaystyle\int (\vec{v}\cdot\vec{v})f(\vec{x},\vec{v},t)d\vec{v}$

ID:(8460, 0)


Tension tensor
Equation

>Top, >Model


If the parameters are calculated by averaging over the speed using

$ \chi_k(\vec{x},t) =\displaystyle\frac{1}{c(\vec{x},t)}\displaystyle\int d\vec{v} f(\vec{x},\vec{v},t) \chi_k(\vec{x},\vec{v},t)$



the flow tensor is calculated by integrating the velocity distribution function on all velocities by weighing the velocity differences:

$\sigma_{ij} = m\displaystyle\int (v_i-u_i)(v_j-u_j)f(\vec{x},\vec{v},t)d\vec{v}$

ID:(8461, 0)


Lattice Boltzmann Method
Description

>Top


The problem with macro scale systems that are based on microscopic phenomena is that

- macroscopic models are too simple to correctly reflect the dynamics

- microscopic models to describe the macroscopic reality can not be solved analytically and numerical solutions are cumbersome (= require a lot of computational resources)

The Boltzmann lattice method looks for an intermediate path. It is based on the Boltzmann transport equation, rescues the microscopic part via the collision term and implements a simplified structure to calculate the macroscopic results. We speak of a mesoscopic approach where we can, as required, reduce microscopic effort by losing accuracy but saving resources or improving accuracy by investing more resources.

ID:(8488, 0)


D2Q9 Models (2 dimensions, 9 points)
Image

>Top


El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n

$\vec{e}_0=(0,0)$

\\n\\nen las esquinas\\n\\n

$\vec{e}_1=(1,0)$

(E),\\n

$\vec{e}_2=(0,1)$

(N), \\n

$\vec{e}_3=(-1,0)$

(W) y \\n

$\vec{e}_4=(0,-1)$

(S)\\n\\ny en las diagonales\\n\\n

$\vec{e}_5=(1,1)$

(NE), \\n

$\vec{e}_6=(-1,1)$

(SE), \\n

$\vec{e}_7=(-1,-1)$

(SW) y \\n

$\vec{e}_8=(1,-1)$

(NW)

lo que se representa en la siguiente gráfica:

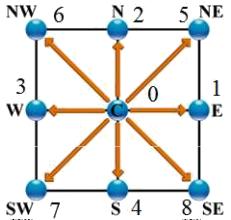
ID:(8496, 0)


D3Q15 Models (3 dimensions, 15 points)
Image

>Top


The D3Q15 model is a two-dimensional model (D3) in which the node (central point) is connected in nodes along Cartesian axes\\n\\n

$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) (0,0,-1)$

\\n\\nand in the corners of the bucket\\n\\n

$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$



which is represented in the following graph:

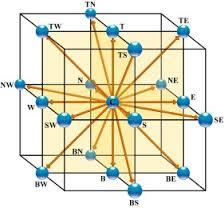
It is easy to build models of type D3Q19 (including side edge halves) or D3Q27 (all possible points).

ID:(8497, 0)


Discretization function
Equation

>Top, >Model


In the case of the discretization in the LBM models we work not with functions of the speed if not with discrete components. In this way the i component is defined by:

$f_i(\vec{x},t)=w_if(\vec{x},\vec{v}_i,t)$

where w_i is the relative weight.

ID:(8466, 0)


Streaming
Equation

>Top, >Model


In the streaming process the particles are moved according to their velocity directions to neighboring cells

$f_i(\vec{x},t)\leftarrow f_i(\vec{x}+ce_i\delta t,t+\delta t)$

where \vec{x} is the position, t time, \vec{e} _i the direction of the grid and c the speed.

ID:(9150, 0)


Rebound in walls orthogonal to the network
Image

>Top


If the collision does not occur at the point of the network, but at a distance \Delta:

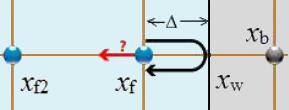
\\n\\nthen the function must consider the offset by weighting the contributions\\n\\n

$f_i(x_f,t+\delta t)=\displaystyle\frac{(1-\Delta)f_{-i}(x_f,t)+\Delta(f_{-i}(x_b,t)+f_{-i}(x_{f2},t)}{1+\Delta}$

ID:(8499, 0)


Rebound on walls with inclination
Image

>Top


If the wall shows an inclination with respect to the network it must be modeled in a more complex form:


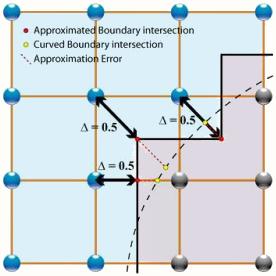
More general edge

First, an approximate boundary must be defined to allow the necessary edge equations to be established. Then they must be applied in the process of steraming.

ID:(8500, 0)


Example of Streaming Equations
Description

>Top


In the case of a D2Q9 system we have the 9 values f_i that we have named as O, N, E, S, W, NE, SE, SW, NW. If the number of particles in position (n,m) is denoted as f_i(j,k) we have that the equations are

```

N[x,y] = N[x,y-1]

NW[x,y] = NW[x+1,y-1]

E[x,y] = E[x-1,y]

NE[x,y] = NE[x-1,y-1]

S[x,y] = S[x,y+1]

SE[x,y] = SE[x-1,y+1]

W[x,y] = W[x+1,y]

SW[x,y] = SW[x+1,y+1]

```

ID:(9151, 0)


Ejemplo de elemento de Colisión
Description

>Top


In case D2Q9 the term collision is calculated by summing the different factors

$f_i^{eq}=\rho\omega_i\left(1+\displaystyle\frac{3\vec{u}\cdot\vec{e}_i}{c}+\displaystyle\frac{9(\vec{u}\cdot\vec{e}_i)^2}{2c^2}-\displaystyle\frac{3u^2}{2c^2}\right)$

so you have for each cell

```

O = O+w(4rho/9)(1-3u2/2) - O)

E = E+w(rho/9)(1 + u_x/3+5u_x^2-3u2/2)-E)

W = W+w(rho/9)(1 - u_x/3+5u_x^2-3u2/2)-W)

N = N+w(rho/9)(1 + u_y/3+5u_y^2-3u2/2)-N)

S = S+w(rho/9)(1 - u_y/3+5u_y^2-3u2/2)-S)

NE = NE+w(rho/36)(1+u_x/3+u_y/3+5(u2+2u_xu_y)/2-3u2/2) - NE)

SE = SE+w(rho/36)(1+u_x/3-u_y/3+5(u2-2u_xu_y)/2-3u2/2) - SE)

NW = NW+w(rho/36)(1-u_x/3+u_y/3+5(u2-2u_xu_y)/2-3u2/2) - NW)

SW = SW+w(rho/36)(1-u_x/3-u_y/3+5(u2+2u_xu_y)/2-3u2/2) - SW)

```

with

```

u2 = u_x^2+u_y^2

```

ID:(9155, 0)


LBM equation in the relaxation approximation
Equation

>Top, >Model


In the relaxation approximation, it is assumed that the distribution f_i(\vec{x},t) tends to relax at a time \tau to an equilibrium distribution f_i^{eq}(\vec{x},t) according to equation\\n\\n

$\displaystyle\frac{df_i}{dt}=-\displaystyle\frac{f_i-f_i^{eq}}{\tau}$



which has in the discrete approximation the equation

$f_i(\vec{x}+c\vec{e_i}\delta t,t+\delta t)=f_i(\vec{x},t)+\displaystyle\frac{1}{\tau}(f_i^{eq}(\vec{x},t)-f_i(\vec{x},t))\delta t$

where the term of the differences in the distribution functions represents the collisions.

ID:(8489, 0)


Distribution in Balance (Gas of Particles)
Equation

>Top, >Model


The equilibrium distribution can be approximated by a distribution of Maxwell Boltzmann

$f_i^{eq}=\displaystyle\frac{m}{2\pi kT}e^{-m|c\vec{e}_i-\vec{u}|^2/2kT}$

Where m is the mass of the particle, T the system temperature and k the Boltzmann constant.

ID:(8490, 0)


Bhatnagar-Gross-Krook Approach
Equation

>Top, >Model


En la aproximación Bhatnagar-Gross-Krook la distribución en equilibrio se asume como la de un gas de partículas sin interacción

$f^{(0)}(\vec{x},\vec{v},t)=c(\vec{x},t)\left(\displaystyle\frac{m\beta}{2\pi}\right)^{3/2}e^{-\beta m(\vec{v}-\vec{u}(\vec{x},t))^2/2}$



con \vec{u} la velocidad del flujo, k la constante de Boltzmann, T la temperatura y m la masa de la particula. Si se desarrolla esta expresión en el limite de velocidades \vec{u} comparada con la velocidad de las moleculas c\hat{e}_i se tiene que

$f_i^{eq}=\rho\omega_i\left(1+\displaystyle\frac{3\vec{u}\cdot\vec{e}_i}{c}+\displaystyle\frac{9(\vec{u}\cdot\vec{e}_i)^2}{2c^2}-\displaystyle\frac{3u^2}{2c^2}\right)$

con \omega_i los pesos dados por

Modelo$\omega_i$Index
1DQ3 ? i=0
- ? i=1, 2
2DQ9 4/9 i=0
- 1/9 i=1,...,4
- 1/36 i=5,...,8
3DQ15 1/3 i=0
- 1/18 i=1,...,6
- 1/36 i=7,...,14
3DQ19 ? i=0
- ? i=1,...,6
- ? i=7,...,18

que se determinan asegurando que la distribución equilibrio cumpla las leyes de conservación.

ID:(9084, 0)


Example Hydrodynamic Simulator
Description

>Top


In the case of particles of a liquid, the method LBM allows to develop simulators as shown in the example:

(html file)

ID:(9156, 0)