Si la pared muestra una inclinaci n respecto de la red debe ser modelada en una forma mas compleja:

image

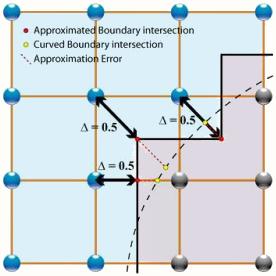
Borde mas general

Primero debe ser definida una frontera aproximada que permita establecer las ecuaciones de borde necesarias. Luego deben ser aplicadas en el proceso de steraming.

Si el choque no ocurre en el punto de la red si no que a una distancia \Delta:

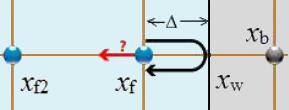
image\\n\\nentonces la funci n debe considerar el desfase ponderando las contribuciones\\n\\n

$f_i(x_f,t+\delta t)=\displaystyle\frac{(1-\Delta)f_{-i}(x_f,t)+\Delta(f_{-i}(x_b,t)+f_{-i}(x_{f2},t)}{1+\Delta}$

En el proceso de streaming se desplazan las part culas seg n sus direcciones de velocidades a las celdas vecinas

equation

donde \vec{x} es la posici n, t el tiempo, \delta t el incremento en el tiempo, \vec{e}_i la direcci n de la grilla y c la velocidad.

En el caso de un sistema D2Q9 se tienen los 9 valores f_i que hemos acotado como O, N, E, S, W, NE, SE, SW, NW. Si el numero de part culas en la posici n (n,m) se denota como f_i(j.k) se tiene que las ecuaciones son

```

N[x,y] = N[x,y-1]

NW[x,y] = NW[x+1,y-1]

E[x,y] = E[x-1,y]

NE[x,y] = NE[x-1,y-1]

S[x,y] = S[x,y+1]

SE[x,y] = SE[x-1,y+1]

W[x,y] = W[x+1,y]

SW[x,y] = SW[x+1,y+1]

```