Ecuación de Transferencia Radiativa
Storyboard 
El transporte de fotones por materia (incluido tejido biologico) puede ser modelado mediante la ecuación de transporte radiativo (Radiative transfer equation - RTE).
ID:(1033, 0)
Radiancia en Función de la Radiancia Espectral
Ecuación 
La radiancia espectral $L_{
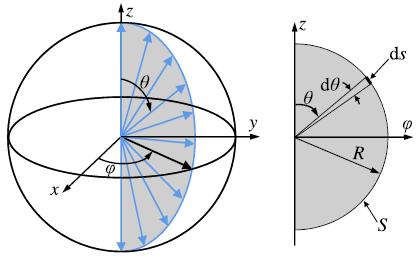
u}(\vec{x},\hat{n},t)$ en un punto $\vec{x}$ y tiempo $t$ es la energía por área $da$ de los fotones de frecuencia entre $
u$ y $
u+d
u$ emitida durante un tiempo $dt$ en una dirección $\hat{n}$ en un angulo solido $d\Omega$.
Si se integra la radiancia espectral en la frecuencia se obtiene la radiacia total:
| $L_i(\vec{x},\hat{n},t)=\displaystyle\int d\nu L_{i,\nu}(\vec{x},\hat{n},t)$ |
ID:(8482, 0)
Flujo radiante
Ecuación 
La integración de la radiancia $L$ sobre el angulo solido $d\Omega$ nos da el flujo radiativo $\Phi$
| $\Phi(\vec{x},t)=\displaystyle\int_{4\pi} L(\vec{x},\hat{n},t)d\Omega=\sum_iL_i(\vec{x},\hat{n},t)$ |
ID:(8483, 0)
Definición de Bordes en D2Q7
Imagen 
Las consiciones de borde en el caso D2Q7 son algo mas complejas por no existir una línea vertical simple. Por ello se deben ir empelando puntos para conformar el borde:
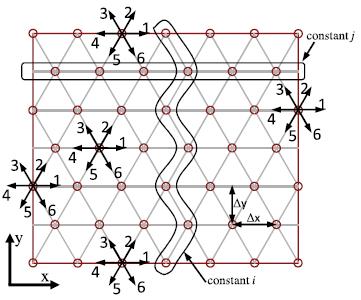
ID:(8564, 0)
Radiancia en Función de Flujo radiativo
Ecuación 
La radiancia es la derivada del flujo radiativo en el angulo y en la sección de superficie proyectada $S\cos\theta$
| $L_i(\vec{x},t)=\displaystyle\frac{\partial^2\Phi_i(\vec{x},t)}{\partial\Omega\partial S\cos\theta}$ |
ID:(8486, 0)
Flujo radiante en Función de la Energía
Ecuación 
El flujo radiativo es la energía radiativa que por tiempo es irradiado:
| $\Phi(\vec{x},t)=\displaystyle\frac{\partial Q}{\partial t}$ |
ID:(8485, 0)
Intensidad radiativa
Ecuación 
La intensidad radiativa es el flujo radiativo por elemento de angulo solido:
| $I_{\Omega}=\displaystyle\frac{\partial\Phi}{\partial\Omega}$ |
ID:(8484, 0)
Ecuación de Transporte Radiativo (RTE)
Ecuación 
La ecuación de transporte de los fotones es
| $\displaystyle\frac{1}{c}\displaystyle\frac{\partial}{\partial t}L(\vec{x},\hat{n},t)+\hat{n}\cdot\nabla L(\vec{x},\hat{n},t)=-\mu_tL(\vec{x},\hat{n},t)+\mu_s\int_{4\pi}L(\vec{x},\hat{n}_h,t)P(\hat{n}_h,\hat{n})d\Omega_h+S(\vec{x},\hat{n},t)$ |
donde $\mu_t$ es el coeficiente de absorción y scattering, $c$ la velocidad de la luz, $P(\hat{n}',\hat{n})$ es la función de fase que entrega la probabildiad de que un foton viajando en la dirección $\hat{n}$ sea desviado en la dirección $\hat{n}'$ y $S$ es una fuente de energía radiativa.
ID:(8487, 0)