Modi finden
Storyboard 
Der beste Weg, um die Ähnlichkeit temporärer Segmente zu bestimmen, ist die Korrelation dieser mit dem aktuellen Segment.
Um das Verfahren zu analysieren, wird ein aktuelles Segment genommen, das in der Vergangenheit liegt, um ein späteres Segment zu haben, das verwendet werden kann, um die Qualität der Prognose zu bewerten.
Die Korrelation wird des letzten Segments mit ähnlichen Segmenten in der Vergangenheit durchgeführt, die dieselben Jahreszeiten abdecken. Es wird das Segment ausgewählt, das die höchste Korrelation aufweist.
ID:(1912, 0)
Lesen von Daten aus Bildern
Bedingung 
Um die Daten zu erhalten, müssen alle Bilder durchlaufen werden, wobei die entsprechenden Pixel gelesen werden:
import os
from os.path import exists
from PIL import Image
# build date array
sdate = []
year = 2010
month = 6
while year < 2022 or (year == 2022 and month < 6):
sdate.append(str(year) + \'-\' + str(month).zfill(2))
if month < 12:
month = month + 1
else:
month = 1
year = year + 1
# load data (pixels from each image)
num = 0
val = []
for n in range(len(sdate)):
file_name = \'../NASA/\' + vdir[nm] + \'/\' + vdir[nm] + \'_\' + sdate[n] + \'.PNG\'n if exists(file_name):
im_var = Image.open(file_name)
# if needed resize
var_width, var_height = im_var.size
if var_width != width or var_height != height:
im_resize = im_var.resize((width, height),resample=Image.NEAREST)
im_var = im_resize
pix_var = im_var.load()
if pix_var[i,j] < 255:
val.append(min_var[nm] + (max_var[nm] - min_var[nm])*pix_var[i,j]/254)
else:
val.append(9999)
num = num + 1
if 144 != num:
print(\'Number or records:\',num)
sys.exit()
ID:(14332, 0)
Problem mit fehlenden Daten
Bedingung 
Um fehlende Daten (mit den Werten 9999 oder -9999) zu liefern, fahren wir fort, die Werte zu interpolieren. Liegen sie an den Extremen, wird aus dem Mittelwert der Skala interpoliert:
# Eliminate missing values
x = []
min_range = []
max_range = []
cnt_range = []
delta_range = []
val_range = []
sta = 0
for i in range(len(val)):
# case first point unknown
if i == 0 and (val[0] == 9999 or val[0] == -9999):
min_range.append(0)
cnt_range.append(1)
sta = 1
# no case selected
if sta == 0:
# check if range is starting and setup in case
if val[i] == 9999 or val[i] == -9999:
min_range.append(i)
cnt_range.append(1)
sta = 1
# case in progress
else:
# is finishing
if val[i] != 9999 and val[i] != -9999:
max_range.append(i-1)
delta_range.append(0)
val_range.append(0)
sta = 0
# not finish
else:
cnt_range[len(cnt_range)-1] = cnt_range[len(cnt_range)-1] + 1
x.append(val[i])
# close if case in progress
if sta == 1:
max_range.append(len(val)-1)
delta_range.append(0)
val_range.append(0)
# setup delta and val
for i in range(len(cnt_range)):
# if last point
if max_range[i] == len(x) - 1:
delta_range[i] = (max_var[nm] + min_var[nm])/2
else:
delta_range[i] = x[max_range[i] + 1]
print(\'max\',max_range[i],x[max_range[i] + 1])
# if first point
if min_range[i] == 0:
delta_range[i] = delta_range[i] - (max_var[nm] + min_var[nm])/2
val_range[i] = (max_var[nm] + min_var[nm])/2
else:
delta_range[i] = delta_range[i] - x[min_range[i] - 1]
val_range[i] = x[min_range[i] - 1]
print(\'min\',min_range[i],x[min_range[i] - 1])
for n in range(min_range[i],max_range[i] + 1):
x[n] = val_range[i] + delta_range[i]*(n - min_range[i] + 1)/(max_range[i] - min_range[i] + 2)
ID:(14319, 0)
Berechnung des Trends durch Regression
Bedingung 
Um den Trend innerhalb des Signals zu erhalten, führen wir eine Regression mit allen Zeitpunkten durch, mit denen es modelliert wird:
# Seteo de datos
sxy = 0
sx = 0
sy = 0
sx2 = 0
N = 0
# calculo de sumas
for i in range(nmon):
# calculo de sumas
for i in range(x):
# sumas
sxy = sxy + i*x[i]
sx = sx + i
sy = sy + x[i]
sx2 = sx2 + i**2
N = N + 1
# calculate coefficients
d = N*sx2 - sx**2
if d != 0:
a = (sx2*sy - sx*sxy)/d1
b = (N*sxy - sx*sy)/d1
ID:(14317, 0)
Die Zeitreihen vorbereiten
Bild 
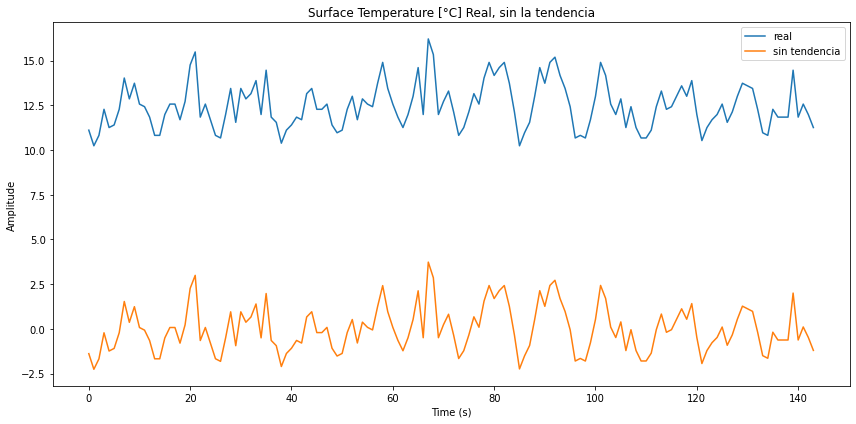
Para obtener los modos se debe primero restar la tendencia. Esto se logra restando la función obtenida de la regresión:
z = []
for i in range(len(x)):
z.append(x[i] - a - b*i)Con ello se obtiene una nueva función que oscila en torno de cero:
ID:(14318, 0)
Berechnung von Modi
Bild 
Los modos se obtienen realizando la transformada de Fourier:
import numpy np from numpy.fft import fft, ifft Z = fft(z) T = len(Z) t = np.arange(N) df = 1/T
con lo que se obtiene un diagrama en que se ve cada modo:
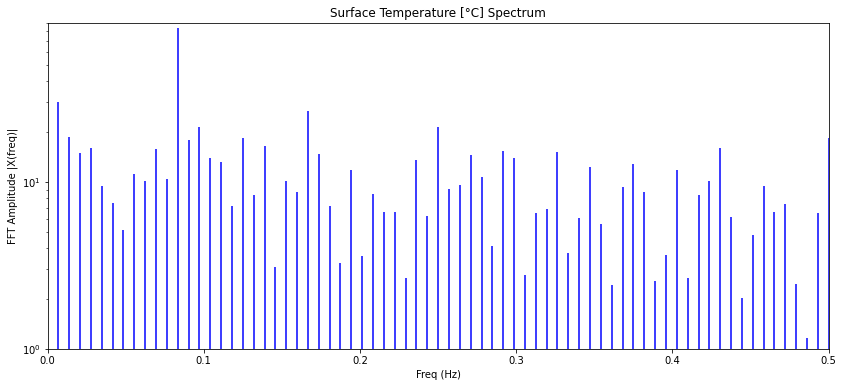
Nota: las lineas corresponde a valores complejos. La representación es en función del valor absoluto:
import matplotlib.pyplot as plt plt.figure(figsize = (14, 6)) plt.stem(freq, np.abs(Z), \'b\', markerfmt=\' \', basefmt=\'-b\') plt.title(unt_var[nm]+\' Spectrum\') plt.xlabel(\'Freq (Hz)\') plt.ylabel(\'FFT Amplitude |X(freq)|\') plt.yscale(\'log\') plt.xlim(0,0.5) plt.show()
ID:(14333, 0)
Filterung im Jahresmodus
Bild 
El espectro esta compuesto de tres partes:
- la oscilación anual
- los modos de periodo mayor que un año
- las fluctuaciones
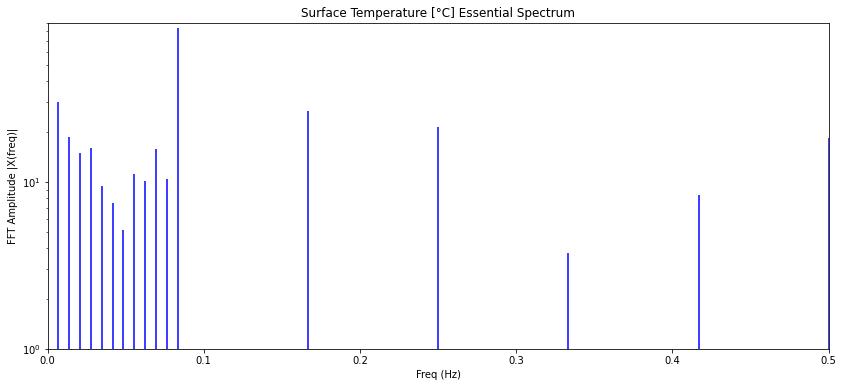
Los primeros son la onda base con frecuencia de 1/12 y sus armónicos. Las frecuencias menores debajo de la frecuencia base y los modos entre los armónicos que corresponden a las fluctuaciones. Para obtener el modelo se eliminan las fluctuaciones lo que se logra simplemente anulando los valores del espectro:
Zm = []
for i in range(len(Z)):
if i < imax:
# frecuencias bajas
Zm.append(Z[i])
elif i % imax == 0:
# modos anuales
Zm.append(Z[i])
else:
# frecuencias altas
Zm.append(complex(0,0))con lo que se obtiene un diagrama en que se ve cada modo:
ID:(14335, 0)
Jährliche Modellmodi
Bild 
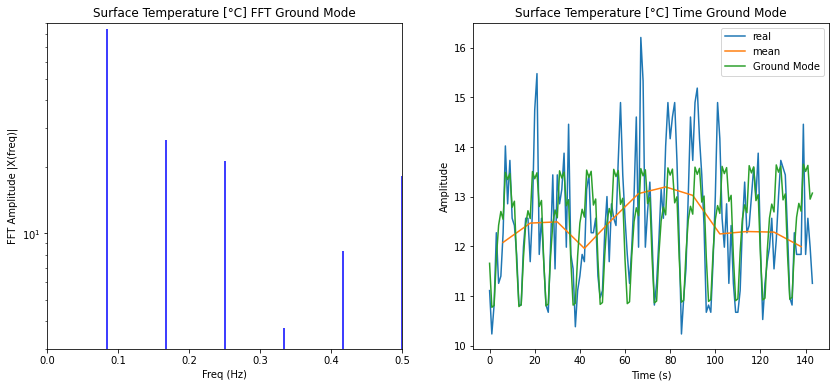
Si se consideran solo los modos anuales se puede filtrar aquella parte de la serie temporal:
ID:(14334, 0)
Jährliche Modellzeitreihen
Bild 
Si se calcula la transformada de Fourier inversa se puede obtener la forma de la curva para estos modos.
from numpy.fft import fft, ifft X = ifft(Z)
En este caso se obtiene una serie temporal de la forma:
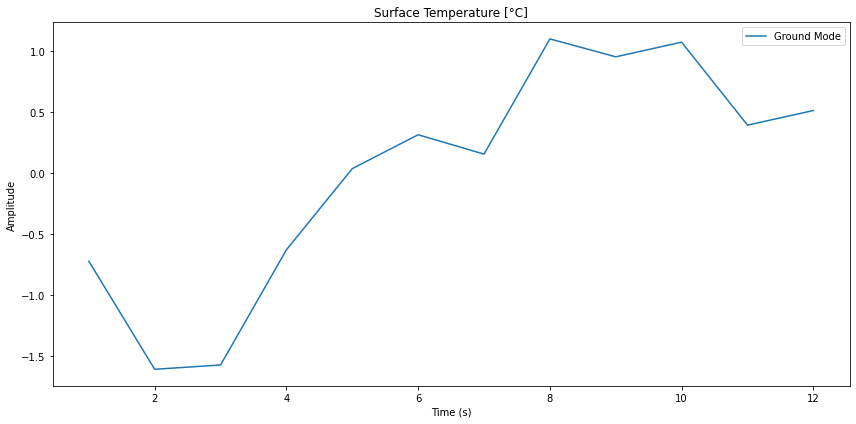
ID:(14338, 0)
Modi des Niederfrequenzmodells
Bild 
Si se consideran solo los modos de frecuencias menores, se puede filtrar aquella parte de la serie temporal:
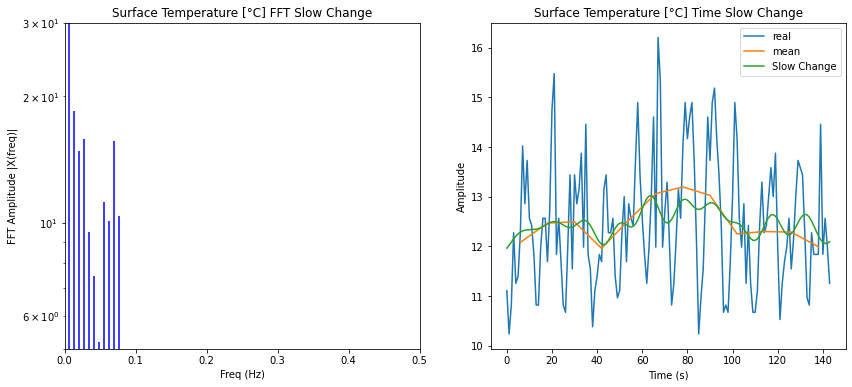
ID:(14336, 0)
Zeitreihen des Nebenfrequenzmodells
Bild 
Si se calcula la transformada de Fourier inversa se puede obtener la forma de la curva para estos modos.
from numpy.fft import fft, ifft X = ifft(Z)
En este caso se obtiene una serie temporal de la forma:
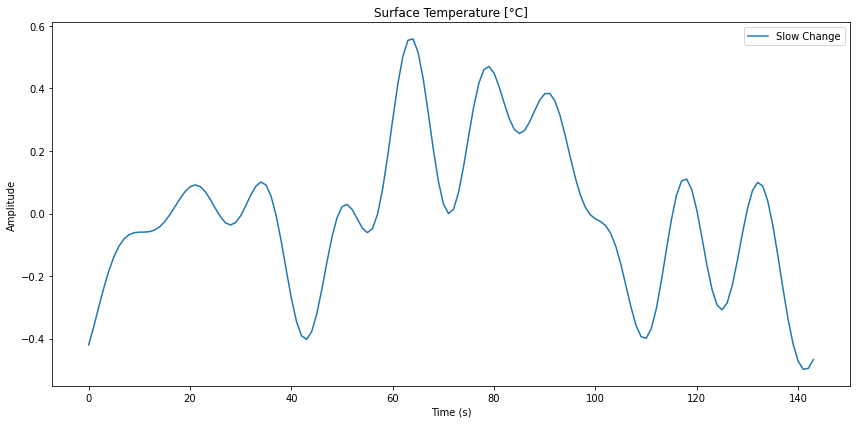
ID:(14340, 0)
Modi des Fluktuationsmodells
Bild 
Si se consideran solo los modos de fluctuación se puede filtrar aquella parte de la serie temporal:
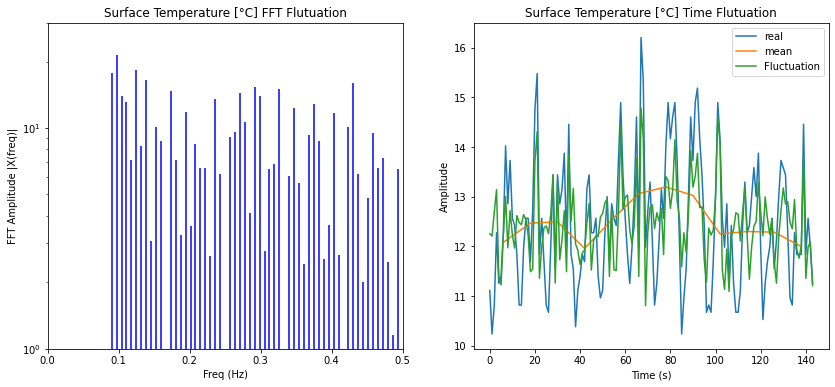
ID:(14337, 0)
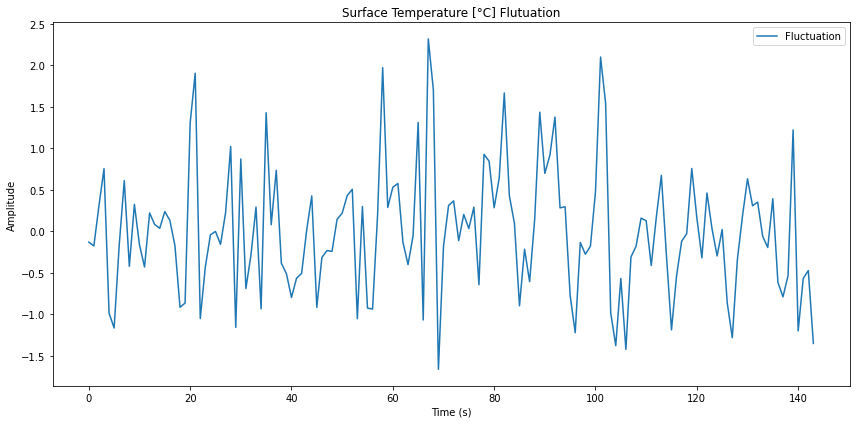
Schwankungen modellieren Zeitreihen
Bild 
Si se calcula la transformada de Fourier inversa se puede obtener la forma de la curva para estos modos.
from numpy.fft import fft, ifft X = ifft(Z)
En este caso se obtiene una serie temporal de la forma:
ID:(14339, 0)
Fluktuationsanalyse
Bild 
Um festzustellen, ob die Fluktuation eine Art Struktur hat, können Segmente von Fluktuationen zwischen verschiedenen Jahren korreliert werden:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
data = {}
col = []
for i in range(0,nmon):
temp = []
for s in range(0,12):
temp.append(Xf[12*i + s])
data[str(i+1)] = temp
col.append(str(i+1))
df = pd.DataFrame(data,columns=col)
dfcorr = df.corr().round(2)
plt.figure(figsize = (12, 12))
plt.title(\'Correlation\')
mask = np.triu(np.ones_like(dfcorr, dtype=bool))
sns.heatmap(dfcorr, annot=True, vmax=1, vmin=-1, center=0, cmap=\'vlag\', mask=mask)
plt.show()Die Ausgabe zeigt alle möglichen Korrelationen:
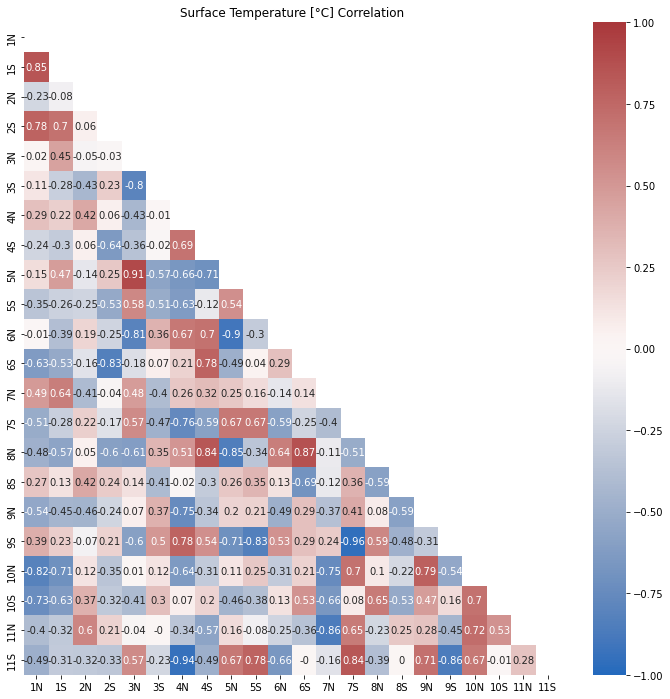
die in diesem Fall kein charakteristisches Wiederholungsmuster zu zeigen scheinen.
ID:(14341, 0)
