Fotones Térmicos
Storyboard 
Fotones termicos significa que hay una distribución homogena de los fotones sobre la red.
ID:(1042, 0)
Caso Photones
Ecuación 
Para el caso en que se consideran fotones térmicos uniformemente distribuidos su número por celda será según la distribución de Bose-Einstein
| f_i^{eq}=\displaystyle\frac{1}{e^{\hbar\omega/kT}-1} |
donde
ID:(8561, 0)
Conductividad Térmica
Ecuación 
La conductividad termica en un medio de Gray es
| k_{bulk}=\displaystyle\frac{1}{3}c_vv_g\Lambda |
ID:(8570, 0)
Definición de Bordes en D2Q7
Imagen 
Las consiciones de borde en el caso D2Q7 son algo mas complejas por no existir una línea vertical simple. Por ello se deben ir empelando puntos para conformar el borde:
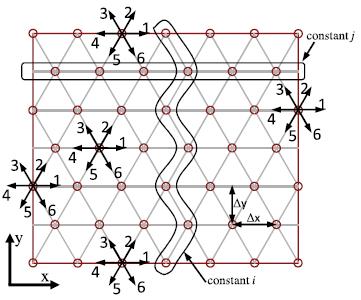
ID:(8564, 0)
Densidad de estados
Ecuación 
La densidad de estados es
| D_{\omega}=\displaystyle\frac{c_v(e^{\chi}-1)^2}{k\chi^2e^{\chi}\Delta\omega} |
con
ID:(8568, 0)
Factores caso Silicon 300K
Descripción 
Los valores caracteristicos
Variables | Valores
----------|---------
Phonon relaxation time (\tau) | 6.53E-12 s
Phonon mean free path (\Lambda) | 41.79E-9 m
Phonon group velocity (v_g) | 6400 m/s
Phonon frequency (\omega) | 8.18E+13 rad/s
Volumetric specific heat (c_v) | 1.66E+6 J/m3 K
Density (\rho) | 2328 kg/m3
Bulk thermal conductivity (k) | 148 W/mk
ID:(8571, 0)
Flujo de Calor
Ecuación 
El flujo de calor en la dirección \vec{n} es
| \vec{q}_n(\vec{x},t)=\displaystyle\frac{d}{\pi}[\sum (f_{in}(\vec{x},t)\cos\theta-f_{out}(\vec{x},t)\cos\theta)]\hbar\omega v_gD_{\omega}\Delta\omega |
con \theta entre el fotón y la dirección \vec{n}. D_{\omega} es la densidad de estados, \Delta\omega el ancho de banda de Gray y d el numero de dimensiones del espacio.
ID:(8567, 0)
Temperatura en la aproximación de Gray
Ecuación 
En la aproximación de Gray la temperatura se estima mediante
| T(\vec{x},t)=\displaystyle\frac{\hbar\omega}{k\log\left(\displaystyle\frac{1}{f^{eq}(\vec{x},t)}+1\right)} |
ID:(8566, 0)
Velocidad de Grupo Fotones térmicos en D2Q7
Ecuación 
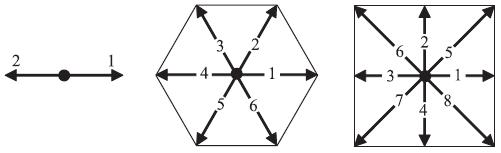
En el caso de fotones termicos las velocidades en las distintas direcciones son
| v_{g,\alpha}=\left[\cos\left((\alpha-1)\displaystyle\frac{\pi}{3}\right),\sin\left((\alpha-1)\displaystyle\frac{\pi}{3}\right)\right]v_g |
con \alpha = 1\dots 6.
ID:(8565, 0)