Vertical Stability
Storyboard 
The stability of the marine water column depends on both temperature and salinity.
If the temperature increases, the water expands, creating a zone of lower density, causing the volume to tend to float.
Conversely, if salinity increases, density increases, causing the volume to sink.
In this sense, there is a competition between the effects of temperature and salinity, where the volume can try to rise or sink. The latter case is key for the generation of deep currents.
ID:(1524, 0)
Mechanisms
Iframe 
Mechanisms
ID:(15508, 0)
Stability of the water column
Description 
Typically, the density of seawater increases with depth.
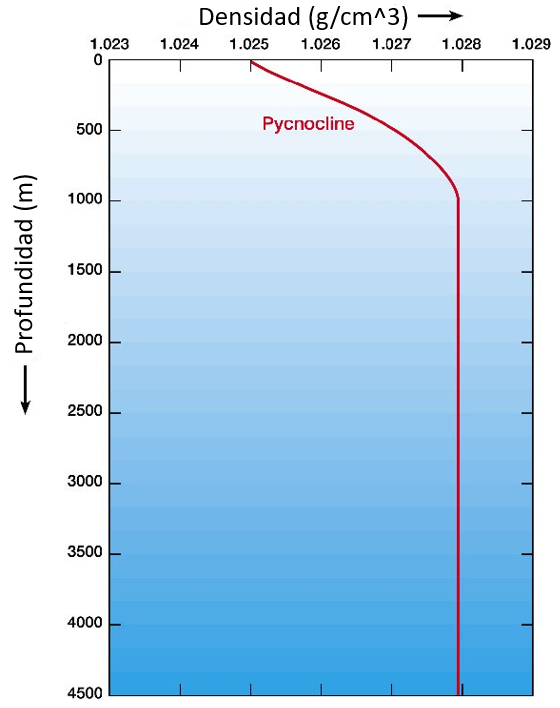
This means that the layers closer to the surface are lighter than the deeper layers. This ensures that these layers float above the deeper layers and do not tend to displace them.
However, fluctuations in temperature and salinity can cause the deeper layers to become less dense than the upper layers. This creates an unstable situation, as these layers tend to float and emerge above the upper layers.
It is only in situations where the density is constant or increases with depth that the system is stable.
On the other hand, when a system becomes unstable, it means that in the presence of a disturbance, it may collapse, but if left undisturbed, it can maintain its current state.
ID:(12045, 0)
Temperature and salinity variation
Top 
The increase in the temperature variation (\Delta T) leads to thermal expansion, causing the volume variation by temperature (\Delta V_T) to increase relative to the volumen (V) with the thermic dilatation coefficient (k_T), as shown in:
| k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T } |
Similarly, the increase in the variación de la salinidad (\Delta s) due to mass causes the density variation (\Delta\rho) to increase relative to the sea water density (\rho) with the salinity coefficient (k_s), as shown in:
| k_s =\displaystyle\frac{ 1 }{ \rho }\displaystyle\frac{ \Delta\rho }{ \Delta s } |
This expression is equivalent to the expression in which the volume variation due to salinity (\Delta V_s) decreases (negative value), as shown in:
| k_s \equiv - \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_s }{ \Delta s } |
Therefore, the role of temperature and salinity is crucial, as they can cause the oceanic water column to become unstable, leading a volume element to start floating or sinking, thereby reversing the column.
ID:(15514, 0)
Instability in water in case of temperature difference
Description 
When heating water in a pot, a region of lower density forms at the bottom near the heat source. This region begins to rise, attempting to displace the cooler, denser layer above it, which in turn tends to sink.
Once the temperature difference between the surface and the bottom exceeds a critical value, true jets of hotter water start to emerge, reaching the surface and creating space for the cooler surface water to descend towards the bottom:
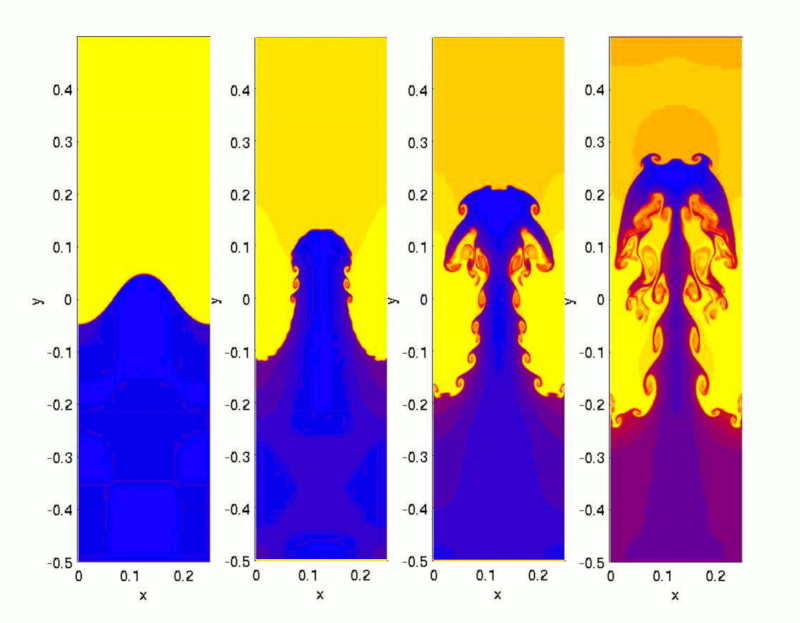
ID:(12046, 0)
Stability of the seawater column
Image 
In the case of seawater, not only can there be variations in temperature, but also in salinity. Salinity generally increases density, so processes that reduce salinity in the depth can lead to instabilities.
In this case, there are regions where water with higher salinity sinks while water with lower concentration rises. These sinking salt zones are called salt fingers and can be seen in the following graph generated through simulation:
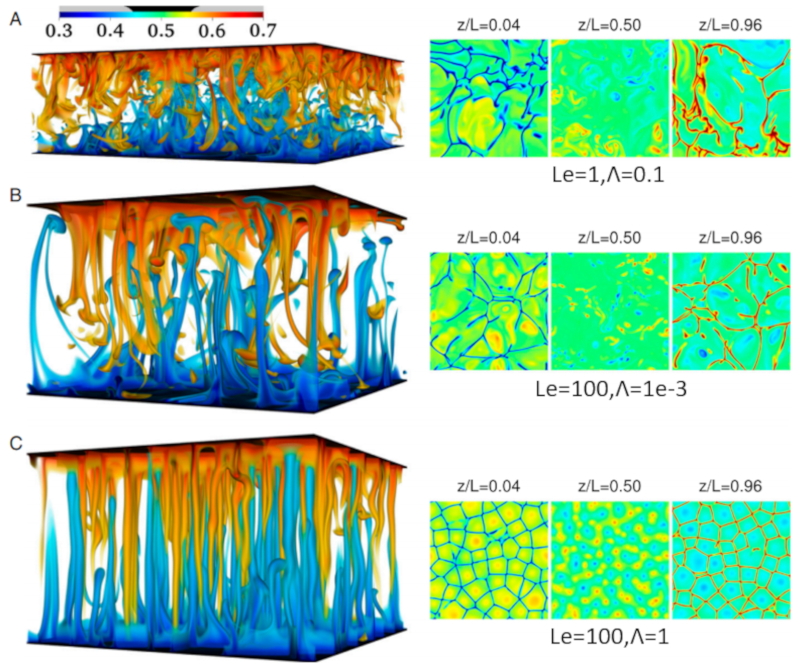
ID:(12051, 0)
Diffusion concept
Description 
Diffusion corresponds to the random motion of molecules gradually spreading out in space. The multiple collisions frequently cause them to change their travel direction, leading to a slow expansion. To describe this movement, statistical concepts are employed, such as describing the region where the majority of particles are located using the root-mean-square deviation. In fact, this root-mean-square deviation increases linearly over time:

The proportionality constant is known as the diffusion coefficient.
The concept is also used to describe how properties of particles, such as momentum and energy, propagate within a system. In this case, the spatial distribution of particles remains unchanged, but the spatial distribution of the considered parameter is affected.
ID:(13405, 0)
Rayleigh number for temperature and stability
Top 
When water is heated in a pot, the water near the bottom begins to warm up, causing it to expand by ($$) according to the thermal expansion relationship, which complies with the thermic dilatation coefficient (k_T), the volumen (V), and the temperature variation (\Delta T) through:
| k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T } |
the buoyancy force (F_b) is proportional to the displaced volume and can be approximately expressed as:
F_b \sim g \Delta V \sim k_T V \Delta T
By analyzing the units, we can observe that the factor
\Delta V g \rightarrow \displaystyle\frac{m^4}{s^2}
is the square of a diffusion constant. Therefore, instability can be understood as the dominance of the diffusion constant of the moment (D_p) of convection compared to the thermal diffusion constant (D_T) necessary to increase temperature and the loss of momentum due to viscosity.
Therefore, if the following proportion:
\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T
is much greater than unity, convection will dominate. In this sense, it makes sense to define a characteristic dimensionless number known as the rayleigh number for temperature (Ra_T):
| Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T |
In the case of a system without boundaries, it has been shown that the critical limit for instability occurs when the Rayleigh number exceeds Ra_L=657.51. However, this limit depends on the geometry of the system, and in the case of a cylinder (like an open pot), it has been demonstrated to be unstable when Ra_L=1,100.65.
ID:(15510, 0)
Lambda factor
Top 
The tendency for an element of oceanic water to float due to increased temperature or to sink due to increased salinity is represented in the following diagram:
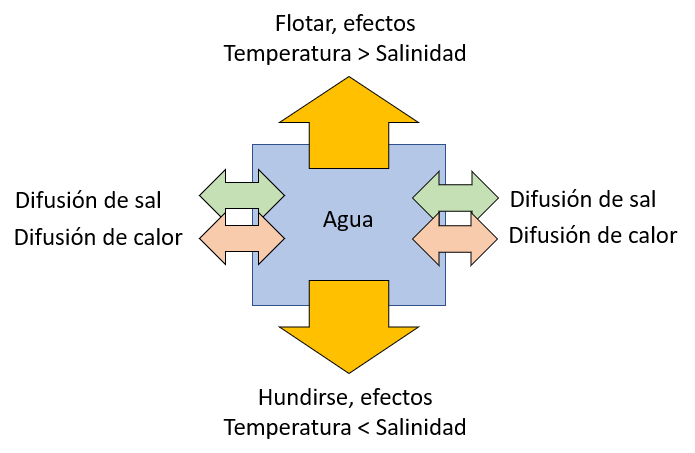
To study the situation, we introduce the lambda factor (\Lambda) as the proportion of the rayleigh number for temperature (Ra_T) and the numero de Rayleigh para la salinidad (Ra_s):
\Lambda = \displaystyle\frac{Ra_T}{Ra_s} = \displaystyle\frac{k_T \Delta T}{k_s \Delta s}
Since the rayleigh number for temperature (Ra_T) depends on the gravitational Acceleration (g), the thermic dilatation coefficient (k_T), the temperature variation (\Delta T), the diffusion constant of the moment (D_p), and the thermal diffusion constant (D_T) through the equation:
| Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T |
and the numero de Rayleigh para la salinidad (Ra_s) depends on the salinity coefficient (k_s), the variación de la salinidad (\Delta s), and the particle diffusion constant (D_N) through the equation:
| Ra_s \equiv\displaystyle\frac{ g k_s h ^3 }{ D_p D_N } \Delta s |
we obtain the relationship for the lambda factor (\Lambda) through:
| \Lambda \equiv \displaystyle\frac{ k_T \Delta T }{ k_s \Delta s } |
ID:(15511, 0)
Lewis number
Top 
The numero de Lewis (Le) compares the thermal diffusion constant (D_T), which depends on the ocean thermal conduction (\lambda_T), the specific heat (c), and the sea water density (\rho), as per:
| D_T \equiv \displaystyle\frac{ \lambda_T }{ \rho c } |
with the particle diffusion constant (D_N), which depends on the particle mobility (\mu), the boltzmann constant (k_B), and the absolute temperature (T), as per:
| D_N \equiv \mu k_B T |
Therefore, it is defined as:
| Le \equiv \displaystyle\frac{ D_T }{ D_N } |
ID:(15512, 0)
Stability condition
Top 
To keep the system stable, it's necessary that the diffusion of energy (temperature) and salinity don't generate a the buoyancy force (F_b) large enough to invert the column. This is achieved when the lambda factor (\Lambda) is greater than the numero de Lewis (Le).
Therefore, the system is stable if the following condition is met:
| Le < \Lambda |
It's important to note that the number factor depends on temperature and salinity, so if these variables vary, the system may reach a point of instability.
ID:(15515, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
D_N \equiv \mu k_B T
D_N = mu * k_B * T
D_p \equiv \displaystyle\frac{ \eta }{ \rho }
D_p = eta / rho
D_T \equiv \displaystyle\frac{ \lambda_T }{ \rho c }
D_T = lambda_T /( rho * c )
k_s \equiv - \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_s }{ \Delta s }
k_s = - DV_s /( Ds * V )
k_s =\displaystyle\frac{ 1 }{ \rho }\displaystyle\frac{ \Delta\rho }{ \Delta s }
k_s = Drho /( Ds * rho )
k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T }
k_T = DV_T /( DT * V )
\Lambda \equiv \displaystyle\frac{ k_T \Delta T }{ k_s \Delta s }
Lambda = k_T * DT /( k_s * Ds )
Le < \Lambda
Le < Lambda
Le \equiv \displaystyle\frac{ D_T }{ D_N }
Le = D_T / D_N
Ra_s \equiv\displaystyle\frac{ g k_s h ^3 }{ D_p D_N } \Delta s
Ra_s = g * k_s * Ds * h ^3/( D_p * D_N )
Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T
Ra_T = g * k_T * DT * h ^3/( D_p * D_T )
ID:(15509, 0)
Thermal expansion
Equation 
To model convection, we must consider that the water near the base of the system heats up, and as a result, expands. This expansion is what ultimately leads to a decrease in density and, therefore, the tendency to float. To describe this, the thermic dilatation coefficient (k_T) is introduced, indicating the proportion by which the volume variation by temperature (\Delta V_T) expands relative to the volumen (V) due to the increase in the temperature variation (\Delta T).
Therefore, we have:
ID:(12050, 0)
Density variation due to the effect of salinity
Equation 
The increase in the temperature variation (\Delta T) results in thermal expansion, leading to an increase in the volume variation by temperature (\Delta V_T) with respect to the volumen (V) as a function of the thermic dilatation coefficient (k_T), as shown in:
| k_T \equiv \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_T }{ \Delta T } |
Similarly, adding salt to water leads to an increase in the variación de la salinidad (\Delta s) relative to the sea water density (\rho) due to the increase in the variación de la salinidad (\Delta s) as a function of the salinity coefficient (k_s), as shown in:
ID:(12053, 0)
Volume variation due to salinity effect
Equation 
The increase in the variación de la salinidad (\Delta s) leads to changes in the density variation (\Delta\rho) relative to the sea water density (\rho) with the salinity coefficient (k_s), as shown in:
| k_s =\displaystyle\frac{ 1 }{ \rho }\displaystyle\frac{ \Delta\rho }{ \Delta s } |
This can be formulated in terms of the equivalent the volume variation due to salinity (\Delta V_s) with respect to the volumen (V), resulting in:
As the sea water density (\rho) is equal to a mass m divided by the volumen (V), expressed as:
\rho =\displaystyle\frac{m}{V}
If we differentiate this expression for a constant mass m, it results in a the density variation (\Delta\rho) as:
\Delta\rho =-\displaystyle\frac{m}{V^2}\Delta V=-\displaystyle\frac{\rho}{V}\Delta V
Therefore, the expression in the salinity coefficient (k_s) with the variación de la salinidad (\Delta s):
| k_s =\displaystyle\frac{ 1 }{ \rho }\displaystyle\frac{ \Delta\rho }{ \Delta s } |
implies:
| k_s \equiv - \displaystyle\frac{ 1 }{ V }\displaystyle\frac{ \Delta V_s }{ \Delta s } |
It's important to note that the sign is negative, meaning that the increase in salinity leads to what is effectively a reduction in volume, causing the volume to tend to sink.
ID:(15513, 0)
Diffusion constant of the moment
Equation 
The movement of a system like water tends to dissipate until the system reaches rest relative to its surroundings. This phenomenon is known as viscosity and competes with the inertia of bodies to maintain movement.
The first term is associated with the viscosity of ocean water (\eta), while the second is related to mass, or in the case of a liquid, with the sea water density (\rho).
Therefore, we introduce the diffusion constant of the moment (D_p) with:
The units are:
\displaystyle\frac{\eta}{\rho} \rightarrow \displaystyle\frac{Pa,s}{kg/m^3} = \displaystyle\frac{m^3 kg,m,s}{s^2m^2kg} = \displaystyle\frac{m^2}{s}
which corresponds to a diffusion constant. The value for water is on the order of 10^{-6} , m^2/s.
ID:(12049, 0)
Temperature diffusion constant
Equation 
The temperature in a system like water tends to diffuse until it is uniform throughout the volume. This diffusion is proportional to the ocean thermal conduction (\lambda_T) and inversely proportional to the sea water density (\rho) and the specific heat (c), which are necessary to increase the temperature.
Therefore, we introduce the thermal diffusion constant (D_T) as:
The units are:
\displaystyle\frac{\lambda_T}{\rho,c} \rightarrow \displaystyle\frac{J/m,s,K}{kg/m^3,J/kg K} = \displaystyle\frac{m^2}{s}
which corresponds to a diffusion constant. The value for water is on the order of 10^{-6} , m^2/s.
ID:(12048, 0)
Particle diffusion constant
Equation 
The diffusion of particles, such as salt, occurs slowly due to the interaction of the particles with the medium. This process depends, on one hand, on the particle mobility (\mu), expressed in (m/s)/N=kg/s, which corresponds to the velocity a particle achieves when a force is applied. On the other hand, it depends on the absolute temperature (T), associated with the velocity the particle can reach.
Therefore, the particle diffusion constant (D_N) for the movement of molecules is:
where k_B=1.34\times 10^{-23} J/K is the boltzmann constant (k_B).
ID:(12054, 0)
Rayleigh number for temperature and stability
Equation 
Stability depends on the buoyancy force (F_b), which is proportional to the volume variation by temperature (\Delta V_T), which along with the gravitational Acceleration (g), needs to be compared with the diffusion constant of the moment (D_p) and the thermal diffusion constant (D_T). If we rewrite the volume variation by temperature (\Delta V_T) in terms of thermal expansion with the thermic dilatation coefficient (k_T), where the volumen (V) is expressed as the cube of the depth (h), we get:
\displaystyle\frac{g \Delta V}{D_T D_p} = \displaystyle\frac{g k_T V}{D_p D_T} \Delta T
This way, we can define the rayleigh number for temperature (Ra_T) with respect to temperature:
ID:(12047, 0)
Rayleigh number for salinity
Equation 
The rayleigh number for temperature (Ra_T) represents the comparison of the volume variation by temperature (\Delta V_T) in terms of the temperature variation (\Delta T) and the thermic dilatation coefficient (k_T) with the thermal diffusion constant (D_T) and the diffusion constant of the moment (D_p):
| Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T |
with the gravitational Acceleration (g). Similarly, a relationship for salinity can be established by replacing the thermic dilatation coefficient (k_T) with the salinity coefficient (k_s) and the thermal diffusion constant (D_T) with the particle diffusion constant (D_N), resulting in the numero de Rayleigh para la salinidad (Ra_s):
ID:(12055, 0)
Lambda factor
Equation 
The key to determining whether the volume of water will tend to float or sink can be studied by comparing the relationship between the rayleigh number for temperature (Ra_T) and the numero de Rayleigh para la salinidad (Ra_s), allowing us to define a characteristic number called the lambda factor (\Lambda).
\Lambda = \displaystyle\frac{Ra_T}{Ra_s}
By using the relationships defining the Rayleigh numbers, it can be shown that the lambda factor (\Lambda) is a function of the thermic dilatation coefficient (k_T), the salinity coefficient (k_s), and the temperature variation (\Delta T) with the variación de la salinidad (\Delta s):
Since the rayleigh number for temperature (Ra_T) depends on the gravitational Acceleration (g), the depth (h), the temperature variation (\Delta T), the diffusion constant of the moment (D_p), and the thermal diffusion constant (D_T), as defined by:
| Ra_T \equiv\displaystyle\frac{ g k_T h ^3 }{ D_p D_T } \Delta T |
and the numero de Rayleigh para la salinidad (Ra_s) depends on the salinity coefficient (k_s) and the variación de la salinidad (\Delta s), as defined by:
| Ra_s \equiv\displaystyle\frac{ g k_s h ^3 }{ D_p D_N } \Delta s |
then, we can assert that
\Lambda = \displaystyle\frac{Ra_T}{Ra_s}
reduces to:
| \Lambda \equiv \displaystyle\frac{ k_T \Delta T }{ k_s \Delta s } |
ID:(12056, 0)
Lewis number
Equation 
The numero de Lewis (Le) compares the thermal diffusion constant (D_T) with the particle diffusion constant (D_N) through:
ID:(12058, 0)
Stability condition
Equation 
The system is stable as long as the lambda factor (\Lambda) is greater than the numero de Lewis (Le), as in this case, the diffusion of energy (temperature) and salinity fails to destabilize the column:
ID:(12057, 0)
