Columna de agua en el mar
Storyboard 
En el caso del océano la densidad del agua, dependiendo de su temperatura y salinidad, vara con la profundidad. Por ello la presión no puede ser calculada con la tradicional formula de presión de la columna de agua. Es necesario considerar el efecto de la variación de la densidad y calcular integrando la masa a lo largo de la columna la presión que se presenta a la profundidad que deseamos estimarla.
ID:(1598, 0)
Caracterización de las capas del océano
Imagen 
El transporte de Ekman lleva a que se desplacen las fronteras que existen entre las capas superficiales y las mas profundas en el océano. Estas se caracterizan por cambios bruscos de parámetros en función de la temperatura. En particular se tienen cambios en:
• Temperatura (termoclina)
• Salinidad (haloclina)
• Densidad (picnoclina)

ID:(11684, 0)
Columna con densidad variable
Imagen 
Para calcular la presión bajo el mar a una profundidad dada se debe primero estimar la masa de un elemento de volumen a una cierta profundidad:
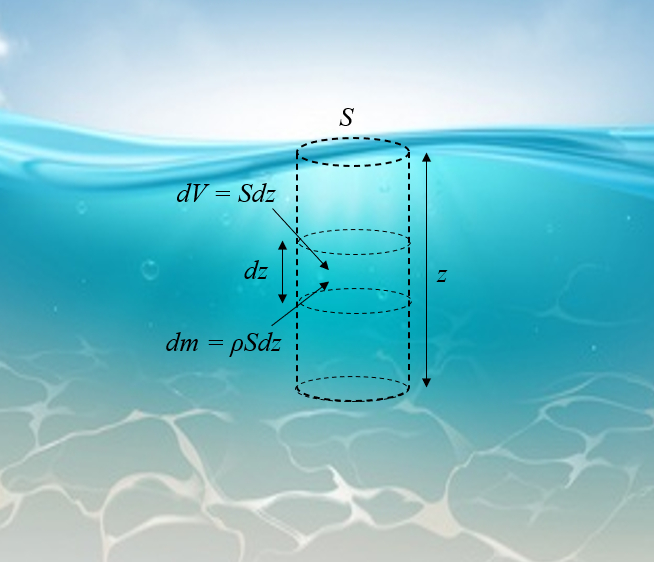
El problema que en este caso la densidad no es constante por lo que no se puede aplicar la relación típica de la presión de la columna de agua.
ID:(12008, 0)
Elemento de masa
Ecuación 
Un elemento de agua de una altura
| dm = \rho S dz |
ID:(12010, 0)
Elemento de fuerza
Ecuación 
Con la definición de la fuerza gravitacional
| F_g = m_g g |
el aumento de la fuerza en función de la masa es
| dF = g \, dm |
ID:(12012, 0)
Variación de la fuerza con la profundidad
Ecuación 
Con la variación de la masa
| dm = \rho S dz |
y la variación de la fuerza en función de la masa
| dF = g \, dm |
con lo que se obtiene
| dF = \rho g S dz |
ID:(12009, 0)
Elemento de presión
Ecuación 
Con la definición de la presión
| p \equiv\displaystyle\frac{ F }{ S } |
la presión aumenta con la fuerza según
| dp =\displaystyle\frac{ dF }{ S } |
en donde se asume que la sección no varia.
ID:(12013, 0)
Relación incremento de presión con profundidad
Ecuación 
Con la definición de la presión
| dF = \rho g S dz |
el aumento de la fuerza
| dp =\displaystyle\frac{ dF }{ S } |
lleva a un aumento de la presión
| dp = \rho g dz |
ID:(12011, 0)
Modelamiento de la densidad
Imagen 
Si se observa la curva de la densidad del agua del océano en función de la profundidad se ve que tiene la forma de un exponencial invertido. En otras palabras se deja comprimir el la parte superior llegando a un limite en que el peso de la columna no lleva a mayor compresión:
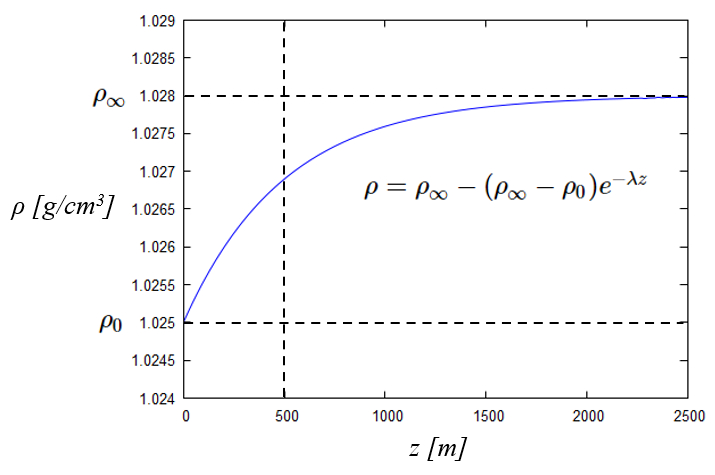
ID:(12014, 0)
Modelo de la densidad del agua marina
Ecuación 
Si se observa la curva de la densidad con la profundidad puede modelar esta con un valor para la densidad en la superficie
| \rho = \rho_{\infty} - (\rho_{\infty}-\rho_0)e^{-\lambda z } |
ID:(11882, 0)
Calculo de presión en la profundidad
Ecuación 
Con el incremento de la presión
| dp = \rho g dz |
se puede mediante integración calcular la presión para cualquier profundidad:
| p = p_0 + g\displaystyle\int_0^z \rho\,du |
ID:(11881, 0)
Presión en función de la profundidad
Ecuación 
Si se emplea la función de la densidad
| \rho = \rho_{\infty} - (\rho_{\infty}-\rho_0)e^{-\lambda z } |
en la ecuación de la presión
| p = p_0 + g\displaystyle\int_0^z \rho\,du |
se obtiene
| p = p_0 + \rho_{\infty} g z - \displaystyle\frac{( \rho_{\infty} - \rho_0 ) g }{ \lambda }(1- e^{- \lambda z }) |
ID:(11883, 0)
0
Video
Video: Columna de agua en el mar
