Utilizador: 
Distribuição do calor transportado pelo calor latente
Descrição 
Se observarmos a distribuição do calor latente transportado sobre a superfície do planeta, podemos notar que ela depende da umidade relativa. Portanto, atinge valores próximos a $150 W/m^2$ sobre os oceanos em zonas equatoriais, diminuindo para $30 W/m^2$ em áreas continentais e chegando a zero em regiões desérticas:
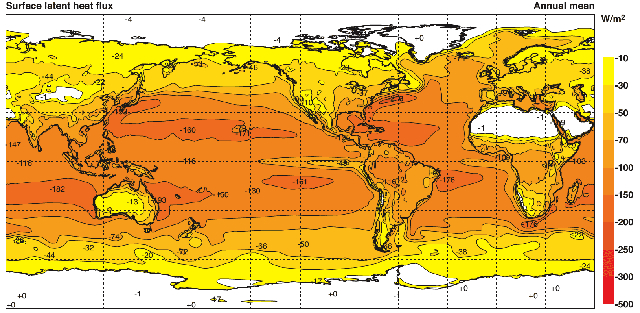
Esses dados são provenientes de uma reanálise de 40 anos realizada por Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, Reino Unido, Projeto de Reanálise do ECMWF (Kallberg et al., 2005).
ID:(9264, 0)
Mecanismo do calor transportado por convecção
Imagem
Quando o vento circula, ele desloca massas de ar com temperatura mais baixa para áreas de temperatura mais alta, resultando em condução e aquecimento do ar. À medida que o ar desloca uma massa de ar e traz uma nova massa com temperatura mais baixa, o processo de transporte continua sem parar, como mostrado na imagem:
Nesse caso, podemos supor que a temperatura do ar corresponde à temperatura na parte inferior da atmosfera, representada por $T_b.
ID:(3076, 0)
Mecanismo de transporte de calor latente
Descrição
Um dos mecanismos chave no processo de fluxo de energia no sistema climático é o processo de evaporação. Nele, a água evapora em um local, retirando energia da superfície, e depois é transportada por convecção até a atmosfera, onde libera novamente essa energia por condensação.
A energia que flui anualmente devido ao transporte de calor latente é igual ao fluxo de $I_E\sim 80,W/m^2$ multiplicado pela superfície do planeta com um raio de $R\sim 6.37\times 10^{+6}m$ e o número de segundos em um ano $t_e=3.15\times 10^{+7}s$.
$Q_e=4\pi R^2 I_E t_e=1.27\times 10^{24},J$
Se o calor latente for igual a $L_v=2256,kJ/kg$ e a densidade da água for $\rho_w=1000,kg/m^3$, podemos calcular o volume de água evaporada por ano:
$V_w=\displaystyle\frac{Q_e}{\rho_wL_v}=5\times 10^{14}m^3$
Dessa água, 87% é evaporada sobre os oceanos, enquanto o restante vem de áreas continentais úmidas. A água retorna à superfície por meio de chuva ou neve. Dos 77% restantes, a maior parte corresponde a chuvas sobre os oceanos, que é ligeiramente superior à proporção da superfície ocupada pelos oceanos.
ID:(9266, 0)
Intensidade do VIS atingindo a superfície do planeta
Equação
De la intensidade média da terra ($I_p$), apenas uma fração chega à superfície da Terra. O fator determinante é La cobertura atmosférica para radiação VIS ($\gamma_v$), portanto la intensidade VIS atingindo a superfície da Terra ($I_{sev}$) é expresso como:
| $ I_t =(1- \gamma ) I_s $ |
Com uma intensidade solar de
$I_s \sim 342 W/m^2$
e uma cobertura atmosférica de
$\gamma_v \sim 0.459$
a radiação que atinge a superfície da Terra é:
$I_{sev} \sim 185 W/m^2$
Isso corresponde a 54,1% da radiação solar. Essa radiação, que leva em conta a perda de intensidade devido à cobertura atmosférica, é conhecida como insolação solar.
ID:(4673, 0)
Calor transportado pelo calor latente
Equação
Além da radiação infravermelha, existe o transporte de calor por meio do calor latente ou fluxo de calor latente (LHF). Esse fenômeno está, em primeira aproximação, relacionado à diferença de pressões de vapor de água entre a superfície da Terra $p_{v,e}$ e a atmosfera $p_{v,a}$:
 $I_E=c_aL_vC_Eu_z\displaystyle\frac{(p_{v,e}-p_{v,a})}{p_a}$ |
Se o fluxo típico de calor transportado pelo calor latente é da ordem de $I_E\sim 80 W/m^2$. Considerando que a concentração molar do ar $c_a\sim 42,4 mol/m^3$, o calor latente de evaporação é $L_v\sim 40,6 kJ/mol$, a velocidade do vento é da ordem de $u_z\sim 8 m/s$, a diferença de pressão de vapor de água é da ordem de $p_{ve}-p_{vb}\sim 1154 Pa$ e a pressão é $p\sim 10^5 Pa$, então o coeficiente de transferência de calor é da ordem de $C_E\sim 5,0\times 10^{-4}$.
ID:(9265, 0)
Calor transportado por convecção
Equação
Além da radiação infravermelha, existe o transporte de calor através da convecção ou fluxo de calor sensível (SHF). Ambos os fenômenos são aproximadamente proporcionais à diferença de temperatura entre a Terra $T_e$ e a parte inferior da atmosfera $T_b$:
| $ I_H = \rho_a c_p C_H u_z ( T_e - T_b )$ |
Se o fluxo típico de calor transportado por convecção está na ordem de $I_H\sim 17 W/m^2$, e considerando a densidade $\rho_a\sim 1.225 kg/m^3$, a capacidade térmica específica $c_p\sim 1006.43 J/kg K$, e a velocidade do vento $u_z\sim 8 m/s$, então, com uma diferença de temperatura de $T_e-T_b\sim 15.2 K$, o coeficiente de transferência de calor está na ordem de $C_H\sim 1.13\times 10^{-4}$.
ID:(4678, 0)
Simplificação transportada por calor latente
Equação
Uma vez que a concentração molar $c_a$ é proporcional à pressão $p_a$, de acordo com:
| $ p = c_m R T $ |
podemos reescrever
| $I_E=c_aL_vC_Eu_z\displaystyle\frac{(p_{v,e}-p_{v,a})}{p_a}$ |
como
| $ I_E = L_v C_E u_z \displaystyle\frac{( p_{v,e} - p_{v,a} )}{ R T_e }$ |
ID:(9275, 0)
Taxa constante de evaporação
Equação
O fluxo de radiação através de elementos de transporte é dado pela equação:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
onde pode ser mostrado que o coeficiente constante de evaporação é dado por:
| $ \kappa_l = L_v C_E \displaystyle\frac{ p_{s,e} }{ R T_e }( RH_e - \gamma_v )$ |
Dado que o fluxo por evaporação é expresso como:
| $I_E=c_aL_vC_Eu_z\displaystyle\frac{(p_{v,e}-p_{v,a})}{p_a}$ |
e buscamos modelar o fluxo como:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
podemos determinar o fator constante como:
| $ \kappa_l = L_v C_E \displaystyle\frac{ p_{s,e} }{ R T_e }( RH_e - \gamma_v )$ |
Assumindo uma concentração molar do ar de $c_a\sim 42.4$, um calor latente molar de $L_v\sim 40.6,kJ/mol$, uma velocidade do vento de $u_z\sim 8,m/s$, uma constante de transporte de calor latente de $C_E\sim 5.0\times 10^{-4}$, uma pressão de vapor de água saturada de $p_{s,e}\sim 1519,Pa$, uma umidade relativa de $RH_e\sim 85%$, uma pressão atmosférica de $p_a\sim 10^5,Pa$ e uma cobertura visível de $\gamma_v\sim 42%$, a constante tem uma ordem de magnitude de $\kappa_c\sim 5.66,J/m^3s$.
ID:(9271, 0)
Coeficiente de temperatura de transporte
Equação
Dado que o fluxo de transporte é dado por
| $ I_H = \rho_a c_p C_H u_z ( T_e - T_b )$ |
e o fluxo de evaporação é
e buscamos modelar o fluxo como
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
o fator de temperatura pode ser determinado como
| $ \kappa_c = \rho_a c_p C_H + C_E p_{s,e} \displaystyle\frac{ \gamma_v L_v ^2}{ R ^2 T_e ^3}$ |
Assumindo que a densidade do ar é $\rho_a\sim 1.225,kg/m^3$, a concentração molar do ar é $c_a\sim 42.4$, o calor latente molar é $L_v\sim 40.6,kJ/mol$, a velocidade do vento é $u_z\sim 8,m/s$, a constante de transporte de calor é $C_H\sim 1.13\times 10^{-4}$ e a constante de transporte de calor latente é $C_E\sim 5.0\times 10^{-4}$, a pressão de vapor de água saturada é $p_{s,e}\sim 1519,Pa$, a umidade relativa é $RH_e\sim 85%$, a pressão atmosférica é $p_a\sim 10^5,Pa$ e a cobertura visível é $\gamma_v\sim 42%$, o aumento no fluxo por grau de diferença de temperatura está na ordem de $\kappa_c\sim 0.47,J/m^3s,K$.
ID:(9272, 0)
Fluxo de condução e evaporativo
Equação
La energia transmitida por condução e evaporação ($I_d$) depende da diferença entre la temperatura do fundo da atmosfera ($T_b$) e ($$), bem como de ($$) e das constantes ($$) e ($$), da seguinte maneira:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
ID:(9270, 0)