Usuario:
Procesos de difusión
Storyboard 
El proceso básico de difusión permite entender como con el tiempo in homogeneidades de concentración tienden a desaparecer.
ID:(1624, 0)
Flujo medio
Ecuación
En un liquido o gas se pueden dar situaciones en que la concentración de algún característica (tipo de sustancia, calor, momento) no sea homogena.\\n\\nEn tal situación sera mas probable que una partículas con dicha característica pasen de la zona de mayor concentración a la de menor por el simple hecho de haber mas. Por ello el flujo dependerá tanto de la diferencia de concentración como de la distancia que debe recorrer. Es decir depende del gradiente.\\n\\nSi existe en un punto
$\Delta c = c(z+\Delta z)-c(z)$
\\n\\nun gradiente\\n\\n
$\displaystyle\frac{c(z+\Delta z)-c(z)}{\Delta z}=\displaystyle\frac{\Delta c}{\Delta z}\sim\displaystyle\frac{\partial c}{\partial z}$
El flujo sera proporcional a dicho gradiente y la constante de proporcionalidad se denomina la constante de difusión.
Por ello con igual a
 $ j = D_N \displaystyle\frac{\Delta c }{\Delta z }$ |
Esta ecuación se denomina la primera ley de Fick.
ID:(12138, 0)
Primera ley de Fick
Ecuación
Para obtener un flujo puntual y no medio se puede estudiar el limite infinitesimal de de los diferenciales del flujo que con constante de difusión de partículas $m^2/s$, densidad de flujo $1/m^2s$, distancia $m$ y variación de la concentración $1/m^3$ es
| $ j = D_N \displaystyle\frac{\Delta c }{\Delta z }$ |
Para ese caso se obtiene lo que se llama la primera ley de Fick que con constante de difusión de partículas $m^2/s$, densidad de flujo $1/m^2s$, distancia $m$ y variación de la concentración $1/m^3$ es
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
ID:(12140, 0)
Calculo de concentraciones
Imagen
Para determinar la concentración en un punto se necesita calcular las cantidades que ingresan y las que salen de un volumen. Por ello para un espacio entre dos posición se considera el flujo que entra en restar lo que sale. Por ello la variación de la cantidad es igual a la concentración por el largo del segmento que es a su vez igual a el flujo por el tiempo considerado:
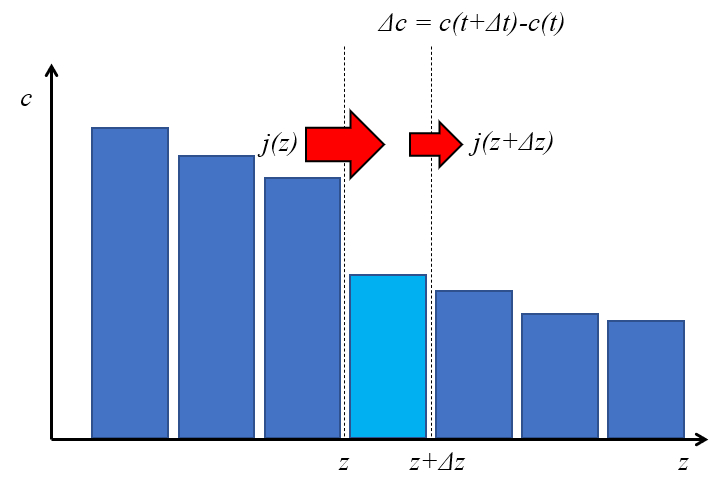
ID:(12141, 0)
Calculo de la evolución de la concentración
Ecuación
Si se considera un elemento de largo
$\Delta c \Delta z = (-j(z) + j(z+\Delta z)) \Delta t = -\Delta j \Delta t$
o con la relación es
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
ID:(12143, 0)
Segunda ley de Fick
Ecuación
Para obtener la concentración puntual se debe pasar en la versión media que con distancia $m$, variación de la concentración $1/m^3$, variación de la densidad de flujo $1/m^2s$ y variación del tiempo $s$ la ecuación
| $ \displaystyle\frac{\Delta c }{\Delta t } = -\displaystyle\frac{\Delta j }{\Delta z }$ |
se pasa a la versión infinitesimal que corresponde a la segunda ley de Fick. Esta es con distancia $m$, variación de la concentración $1/m^3$, variación de la densidad de flujo $1/m^2s$ y variación del tiempo $s$ la ecuación
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
ID:(12144, 0)
Ley de Fick integrada para constante de difusión general
Ecuación
Como la primera ley de Fick que con concentración $1/m^3$, constante de difusión de partículas $m^2/s$, densidad de flujo $1/m^2s$ y posición $m$
| $ j = D\displaystyle\frac{\partial c }{\partial z }$ |
y la segunda ley de Fick que es con concentración $1/m^3$, densidad de flujo $1/m^2s$, posición $m$ y tiempo $s$
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z }$ |
con lo que se obtiene una ecuación integrada para calcular directamente la concentración que con concentración $1/m^3$, densidad de flujo $1/m^2s$, posición $m$ y tiempo $s$ es
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
ID:(12145, 0)
Ley de Fick integrada para constante de difusión constante
Ecuación
Como la ley de Fick para el caso general que es con concentración $1/m^3$, constante de difusión $m^2/s$, posición $m$ y tiempo $s$
| $ \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial }{\partial z }\left( D \displaystyle\frac{\partial c }{\partial z }\right)$ |
para el caso de que la constante de difusión es constante se reduce con concentración $1/m^3$, constante de difusión $m^2/s$, posición $m$ y tiempo $s$ la ecuación es
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
ID:(12146, 0)
Distribución de concentración en el tiempo
Ecuación
Para el caso de la constante de difusión constante la ley general de Fick con concentración $1/m^3$, constante de difusión $m^2/s$, posición $m$ y tiempo $s$
| $ \displaystyle\frac{\partial c }{\partial t } = - D \displaystyle\frac{\partial^2 c }{\partial z^2 }$ |
se logra resolver esta ecuación obtenerse con concentración $1/m^3$, constante de difusión $m^2/s$, posición $m$ y tiempo $s$ la expresión
| $ c_{zt} =\displaystyle\frac{1}{\sqrt{4\pi D_N t }} e^{- z ^2/4 D_N t }$ |
ID:(12147, 0)
Ancho de la distribución
Ecuación
El ancho de la distribución tiene un ancho que con esta dada por la expresión
| $ \sigma =\sqrt{2 D t }$ |
ID:(12149, 0)
Forma de la distribución
Imagen
La distribución obtenida corresponde con concentración en una posición y tiempo $1/m^3$, constante de difusión de partículas $m^2/s$, pi $rad$, posición $m$ y tiempo $s$ a :
| $ c_{zt} =\displaystyle\frac{1}{\sqrt{4\pi D_N t }} e^{- z ^2/4 D_N t }$ |
que corresponde a una distribución de Gauss y que se muestra a continuación.
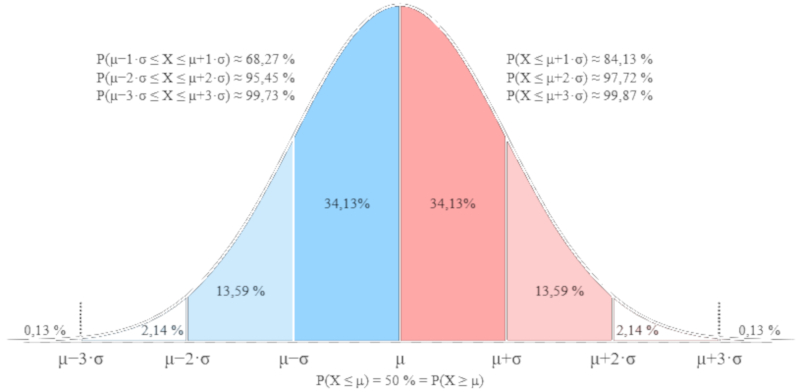
ID:(12142, 0)
0
Video
Video: Procesos de difusión