Utilizador:
Intensidade de emissão NIR da superfície do planeta para o espaço
Equação 
Assim como ocorre com a radiação visível, a atmosfera interage com a radiação infravermelha. De maneira semelhante a como a interação com a atmosfera é modelada para a radiação visível usando la cobertura visível (VIS) ($\gamma_v$)7451, pode-se introduzir ($$)7452 que afeta a radiação infravermelha.
Portanto, la intensidade NIR emitida pela Terra para o espaço ($I_{es}$)6518 é igual a la intensidade NIR emitida pela Terra ($I_e$)6517 ponderado por um fator que depende de ($$)7452, de modo que:
| $ I_{es} =(1- \gamma ) I_s $ |
ID:(4677, 0)
Intensidade de emissão NIR da terra para a atmosfera
Equação
Da radiação terrestre $I_e$, que em sua maioria
| $\lambda > 750\,nm$ |
A fração da radiação que interage com a atmosfera é calculada utilizando a cobertura $\gamma$ através de
| $ I_{esa} = \gamma I_s $ |
ID:(4684, 0)
Intensidade de emissão NIR da superfície da Terra
Equação
Se a Terra está a uma temperatura $T_e$, ela emite radiação de acordo com a lei de Stefan-Boltzmann com uma intensidade dada pela seguinte fórmula:
Onde $\sigma$ é a constante de Stefan-Boltzmann e $\epsilon$ é o coeficiente de emissividade. A constante de Stefan-Boltzmann $\sigma$ tem um valor aproximado de $5.67 \times 10^{-8} W/m^2K^4$, e o coeficiente de emissividade $\epsilon$ representa a eficiência com que a superfície da Terra emite radiação, variando de 0 a 1.
ID:(4676, 0)
Intensidade VIS que interage com a atmosfera
Equação
A intensidade $I$ emitida por um corpo a uma temperatura $T$ é regida pela lei de Stefan-Boltzmann, expressa como:
| $ I = \sigma \epsilon T_b ^4$ |
onde $\epsilon$ é a emissividade e $\sigma$ é a constante de Stefan-Boltzmann. Portanto, no caso da borda inferior da nuvem, que possui uma temperatura $T_b$, a intensidade será:
ID:(4679, 0)
Distribuição do calor transportado por convecção
Descrição
Se observarmos a distribuição do calor transportado por convecção sobre a superfície do planeta, podemos notar que existem níveis mais ou menos constantes. Por um lado, temos as zonas oceânicas e continentais com um fluxo em torno de $17 W/m^2$ (ascendente) e aproximadamente $-30 W/m^2$ (descendente) em áreas cobertas de neve e gelo:
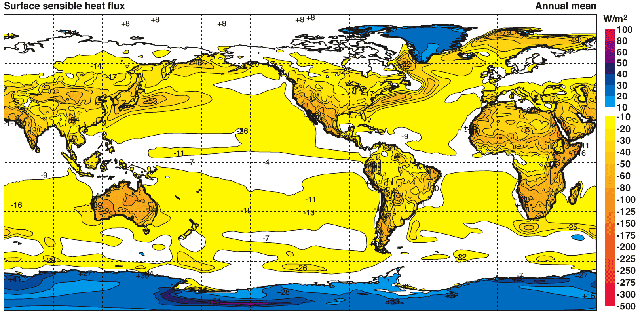
Esses dados são provenientes de uma reanálise de 40 anos realizada por Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, Reino Unido, Projeto de Reanálise do ECMWF (Kallberg et al., 2005).
ID:(9263, 0)
Fluxo de condução e evaporativo
Conceito
Ao modelar la energia transmitida por condução e evaporação ($I_d$)6522, pode-se estabelecer uma relação para o transporte de calor que inclui a diferença entre ($$)6516 e la temperatura do fundo da atmosfera ($T_b$)6519, e ($$)8094, que é crucial no processo. A equação envolve duas constantes, ($$)8093 e ($$)6521, de modo que:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
($$)8093 está na ordem de 10,0 W/m², e ($$)6521 está na ordem de 0,16 W/m²K, com ($$)8094 tipicamente em torno de 8 m/s.
($$)8093 vem principalmente da energia transportada pelo movimento de massas de ar úmido, que liberam energia ao se condensarem. ($$)6521 se origina do transporte de ar através da convecção e da correspondente expansão adiabática, dependendo principalmente do gradiente de temperatura.
ID:(15682, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ I_e = \sigma \epsilon T_e ^4$
I = s * e * T ^4
$ I_b = \sigma \epsilon T_b ^4$
I = s * e * T ^4
$ I_t = \sigma \epsilon T_t ^4$
I = s * e * T ^4
$ I_b = \epsilon \sigma T_b ^4 $
I_b = e * s * T_b ^4
$ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $
I_d =( k_l + k_c *( T_e - T_b ))* u
$ I_e = \epsilon \sigma T_e ^4 $
I_e = e * s * T_e ^4
$ I_{es} =( 1 - \gamma_i ) I_e $
I_es =( 1 - g_i )* I_e
$ I_{esa} = \gamma_i I_e $
I_esa = g_i * I_e
$ I_{esa} = \gamma_i I_e $
I_i = g * I_s
$ I_t = \epsilon \sigma T_t ^4 $
I_t = e * s * T_t ^4
$ I_{es} =(1- \gamma_i ) I_e $
I_t =(1- g )* I_s
ID:(15678, 0)
Intensidade que interage
Equação
La intensidade irradiada ($I_i$)8394 é a fração definida por ($$)8393 de ($$)8390, calculada da seguinte maneira:
| $ I_{esa} = \gamma I_s $ |
| $ I_i = \gamma I_s $ |
ID:(9986, 0)
Intensidade que não interage
Equação
La intensidade irradiada ($I_t$)8392 é igual a ($$)8390 reduzido por ($$)8393, de modo que é:
| $ I_{es} =(1- \gamma ) I_s $ |
| $ I_t =(1- \gamma ) I_s $ |
ID:(10324, 0)
Intensidade dependendo da temperatura (1)
Equação
A Lei de Stefan-Boltzmann estabelece que la intensidade irradiada ($I$)10370 é uma função de la temperatura ($T$)10367, utilizando as constantes la emissividade ($\epsilon$)10369 e la stefan Boltzmann constant ($\sigma$)10368, da seguinte maneira:
| $ I_e = \sigma \epsilon T ^4$ |
| $ I = \sigma \epsilon T ^4$ |
ID:(14479, 1)
Intensidade dependendo da temperatura (2)
Equação
A Lei de Stefan-Boltzmann estabelece que la intensidade irradiada ($I$)10370 é uma função de la temperatura ($T$)10367, utilizando as constantes la emissividade ($\epsilon$)10369 e la stefan Boltzmann constant ($\sigma$)10368, da seguinte maneira:
| $ I = \sigma \epsilon T_b ^4$ |
| $ I = \sigma \epsilon T ^4$ |
ID:(14479, 2)
Intensidade dependendo da temperatura (3)
Equação
A Lei de Stefan-Boltzmann estabelece que la intensidade irradiada ($I$)10370 é uma função de la temperatura ($T$)10367, utilizando as constantes la emissividade ($\epsilon$)10369 e la stefan Boltzmann constant ($\sigma$)10368, da seguinte maneira:
| $ I = \sigma \epsilon T_t ^4$ |
| $ I = \sigma \epsilon T ^4$ |
ID:(14479, 3)
Fluxo de condução e evaporativo
Equação
La energia transmitida por condução e evaporação ($I_d$)6522 depende da diferença entre la temperatura do fundo da atmosfera ($T_b$)6519 e ($$)6516, bem como de ($$)8094 e das constantes ($$)8093 e ($$)6521, da seguinte maneira:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
ID:(9270, 0)