Répartition de la chaleur transportée par la chaleur latente
Définition 
Si nous observons la distribution de la chaleur latente transportée à la surface de la planète, nous pouvons remarquer qu'elle dépend de l'humidité relative. Ainsi, elle atteint des valeurs proches de $150 W/m^2$ sur les océans dans les zones équatoriales, diminue à $30 W/m^2$ dans les régions continentales et atteint zéro dans les zones désertiques :
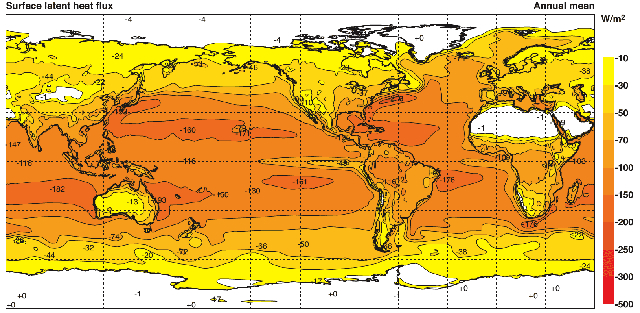
Ces données proviennent d'une réanalyse de 40 ans réalisée par Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005 : ERA-40 Atlas. Reading, Royaume-Uni, Projet de réanalyse de l'ECMWF (Kallberg et al., 2005).
ID:(9264, 0)
Mécanisme de transport de chaleur latente
Noter 
Un des mécanismes clés du processus de transfert d'énergie dans le système climatique est le processus d'évaporation. L'eau s'évapore en un endroit, absorbant ainsi de l'énergie de la surface, puis elle est transportée par convection jusqu'à l'atmosphère où elle libère à nouveau cette énergie par condensation.

L'énergie qui s'écoule annuellement par le transport de chaleur latente est égale au flux de $I_E\sim 80,W/m^2$ multiplié par la surface de la planète avec un rayon de $R\sim 6.37\times 10^{+6}m$ et le nombre de secondes dans une année $t_e=3.15\times 10^{+7}s$.
$Q_e=4\pi R^2 I_E t_e=1.27\times 10^{24},J$
Si la chaleur latente est égale à $L_v=2256,kJ/kg$ et la densité de l'eau est $\rho_w=1000,kg/m^3$, nous pouvons calculer le volume d'eau évaporée par an :
$V_w=\displaystyle\frac{Q_e}{\rho_wL_v}=5\times 10^{14}m^3$
De cette eau, 87% est évaporée sur les océans, tandis que le reste provient des régions continentales humides. L'eau retourne à la surface sous forme de pluie ou de neige. Parmi les 77% restants, la majeure partie correspond aux précipitations sur les océans, légèrement supérieure à la proportion de la surface occupée par les océans.
ID:(9266, 0)
