Utilizador:
Propagação sonora
Storyboard 
A propagação do som no oceano considera tanto a reflexão na superfície e no fundo do oceano quanto as refrações que ocorrem devido às variações de pressão, temperatura e salinidade.
ID:(1550, 0)
Interpretação da refração sonora
Conceito
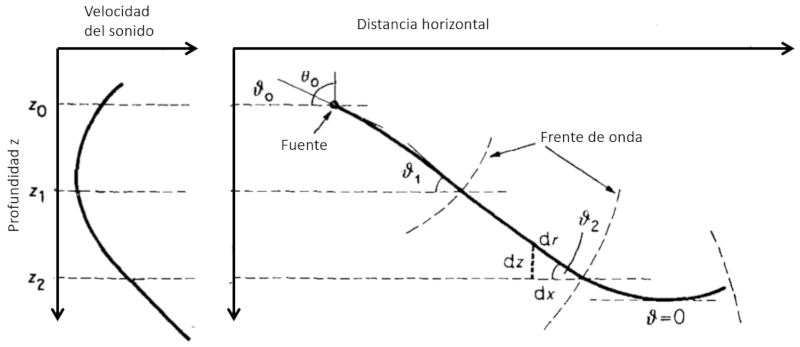
Se observarmos como o som varia com a profundidade e a forma como ele se propaga:
podemos ver que:
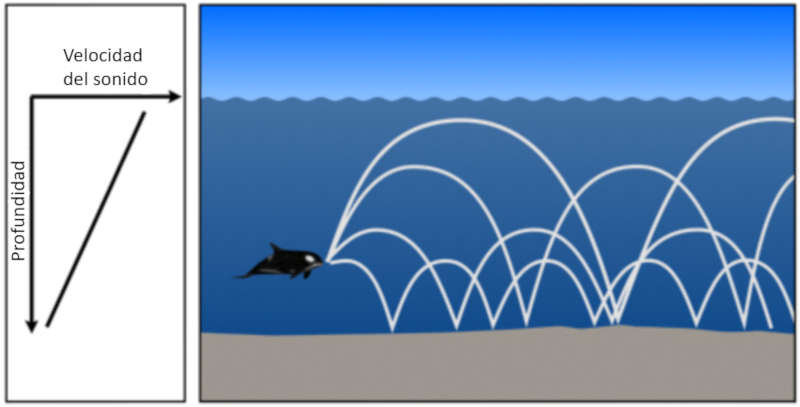
• Se a velocidade do som aumenta com a profundidade, o ângulo entre o feixe e o horizonte tende a diminuir. Isso significa que o som tenderá a diminuir seu declínio até se tornar horizontal e, por simetria, continuará a subir em direção à superfície.
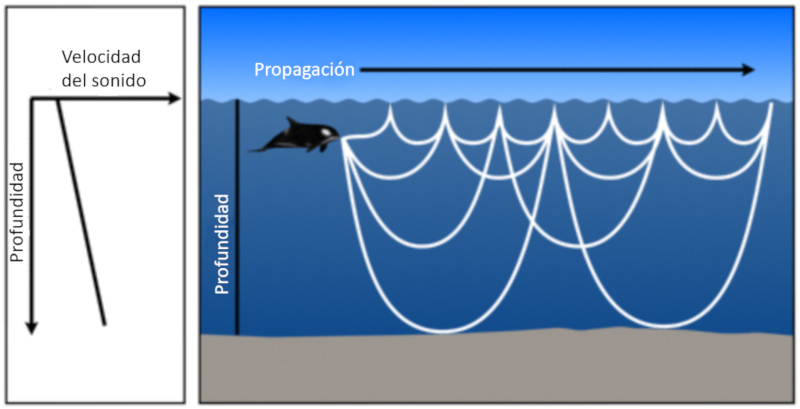
• Se a velocidade do som diminui com a profundidade, o ângulo entre o feixe e o horizonte tende a aumentar. Isso significa que o som tenderá a aumentar seu declínio em direção ao fundo.
ID:(11804, 0)
Se a velocidade do som aumentar
Conceito
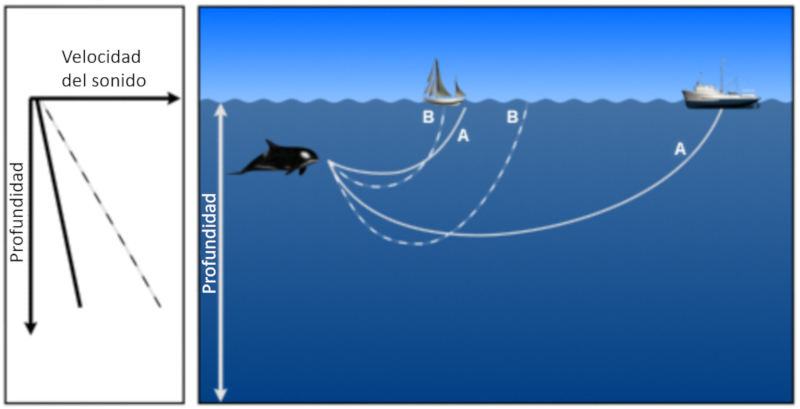
Som emitido em uma profundidade em que a velocidade do som aumenta com a profundidade, os feixes acabam retornando à superfície onde são refletidos e penetram novamente no meio:
ID:(11805, 0)
Se a velocidade do som aumentar e depois diminuir
Conceito
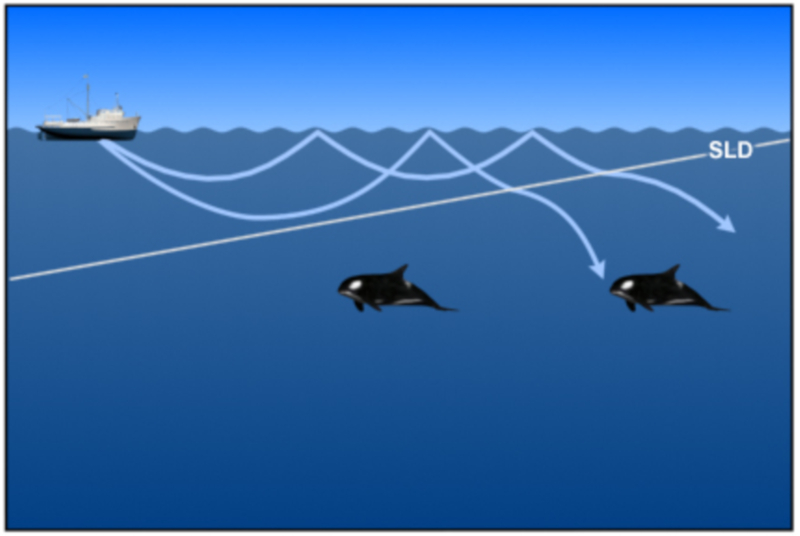
O som emitido em uma profundidade onde a velocidade do som aumenta com a profundidade termina retornando à superfície. No entanto, se a partir de um ponto a velocidade do som diminui, observa-se que os feixes com maior ângulo são refratados em direção às profundezas:
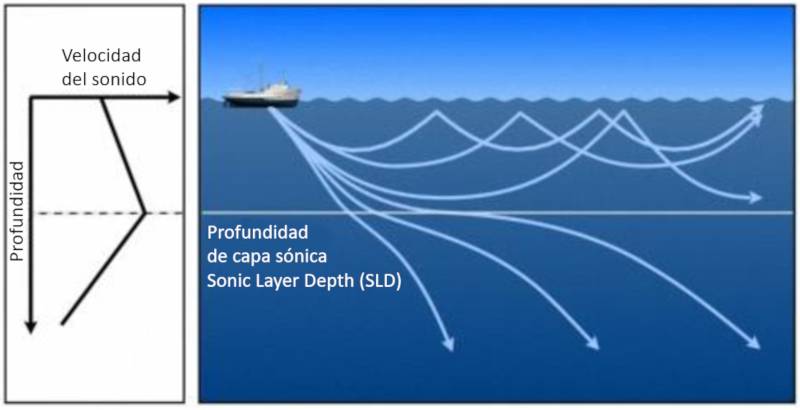
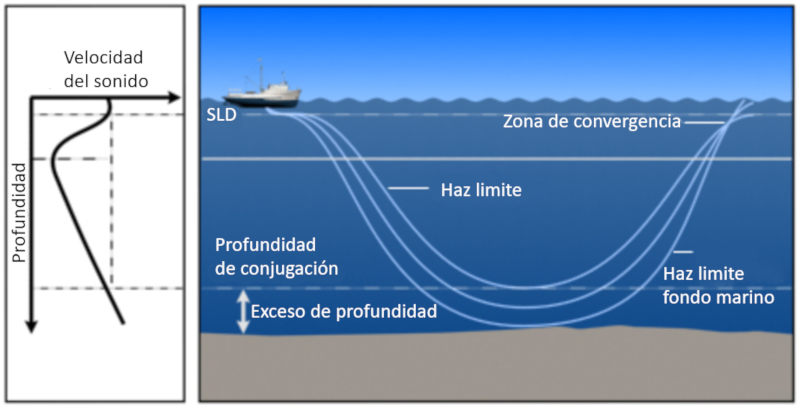
Assim, forma-se uma zona onde os feixes retornam à superfície. Essa profundidade é denominada profundidade da camada sonora SLD (Sonic Layer Depth).
ID:(11806, 0)
Canal de som
Conceito
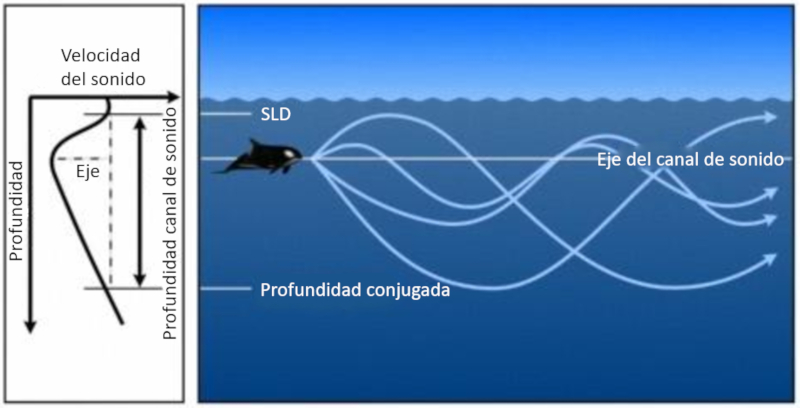
Quando o som diminui e depois aumenta novamente, forma-se uma zona onde tende a retornar à área de velocidade mínima. Essa área é chamada de canal sonoro e se estende da profundidade da camada sônica (SLD) até uma profundidade conjugada:
A profundidade na qual a velocidade do som atinge um mínimo é chamada de eixo do canal sonoro.
Tanto a propagação na zona superior até a profundidade da camada sonora (SLD) quanto no canal sonoro existem. No entanto, a zona superior apresenta o problema de que a superfície amortece o som, tornando o canal sonoro o mais eficaz.
ID:(11807, 0)
Perda de som na camada superior
Conceito
As ondas sonoras que se propagam pela profundidade da camada sonora podem ser filtradas para a zona inferior:
ID:(11808, 0)
Caso de profundidade rasa com velocidade crescente do som
Conceito
Se a água for rasa e a velocidade do som aumentar apenas com a profundidade, então o som retorna à superfície seja por refração ou reflexão no fundo, para depois se refletir na superfície:
ID:(11809, 0)
Caso raso com velocidade decrescente do som
Conceito
Se a água for rasa e a velocidade do som só diminuir com a profundidade, o som tende a ir para o fundo onde é refletido:
ID:(11810, 0)
Temperatura e velocidade do perfil sonoro
Conceito
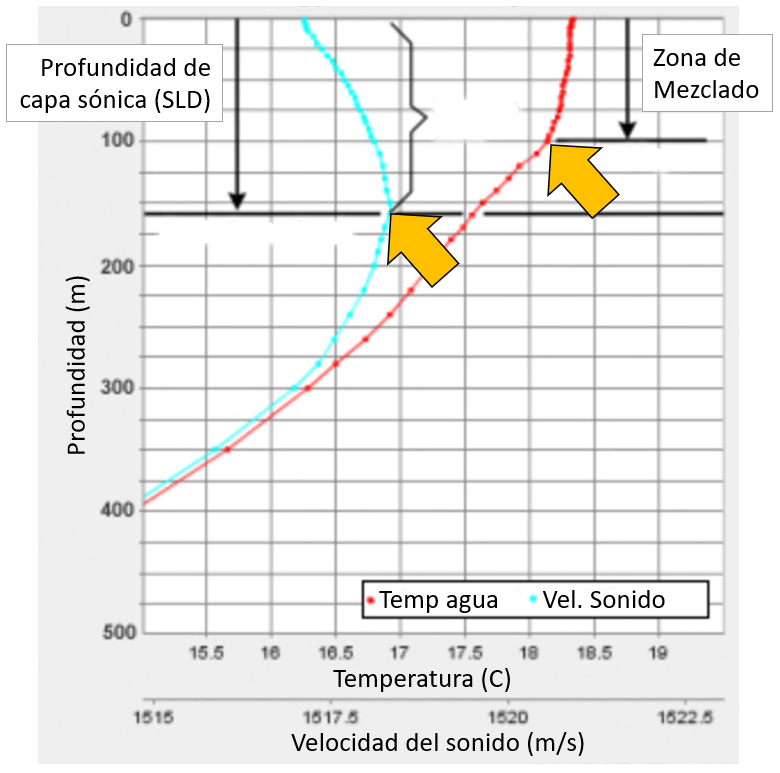
A temperatura atravessa uma zona onde é aproximadamente constante antes de diminuir. Permanece constante na primeira zona devido às turbulências geradas pelo vento, que tendem a misturar a água.
A curva da velocidade do som mostra que ela atinge um máximo que define a profundidade da camada sônica. No seu ponto máximo, a profundidade da camada sônica é definida:
ID:(11811, 0)
Comportamento em maior profundidade
Conceito
Em geral, devido à gravidade, a velocidade do som sempre aumenta com a profundidade. Quando um feixe de som atinge a profundidade da camada sônica SLD (sonic layer depth), eventualmente diverge e retorna à superfície. Os feixes que conseguem retornar à superfície estão situados entre um limite definido pela reflexão no fundo e o limite do feixe que consegue penetrar em camadas mais profundas e eventualmente alcança a superfície:
ID:(11812, 0)
Propagação para distâncias maiores
Conceito
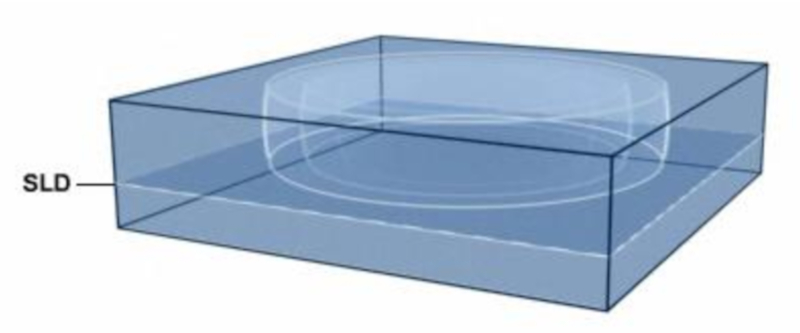
Para o som emitido próximo à superfície, a propagação pode ser modelada como uma propagação esférica. O som de alta frequência tende a amortecer a maiores distâncias, então o modelo esférico é suficiente. No entanto, para o som de baixa frequência, ele pode viajar por toda a bacia. Nesse caso, ele se move através da zona superior até a profundidade da camada acústica (SLD) e/ou através do canal de som. Em ambos os casos, o sistema pode ser modelado usando coordenadas cilíndricas:
ID:(11813, 0)
Perfil sonoro real
Conceito
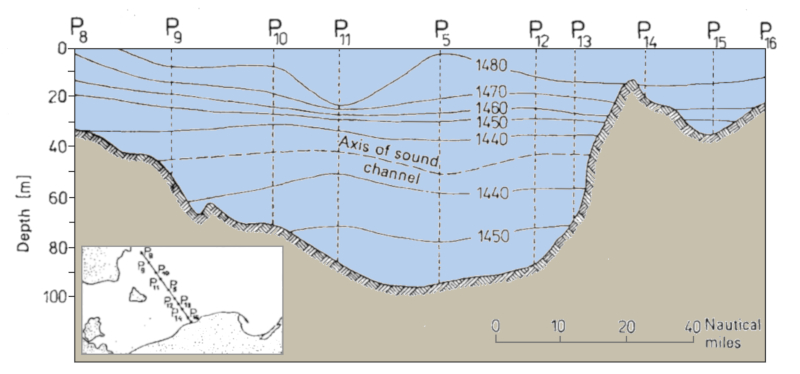
É possível obter um perfil de uma área, como por exemplo um canal, onde são plotadas as velocidades para cada profundidade. Isso permite detectar os canais de som e a profundidade da camada sonora:
ID:(11826, 0)
Modelo
Top
Cálculos
Variáveis
Parâmetros
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado Equação
$ I =\displaystyle\frac{ P }{ 2 \pi r h }$
I = P /(2* pi * r * h )
$\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$
sin( theta_i )/sin( theta_r )= c_i / c_e
$\displaystyle\frac{ d\vartheta }{ dz }=-\displaystyle\frac{\tan \vartheta }{ c } \displaystyle\frac{ dc }{ dz }$
diff( vartheta , z )=-tan( vartheta )*diff( c , z )/ c
ID:(15466, 0)
Refração sonora
Equação
A refração do som ao passar de um meio para outro é geralmente descrita pela lei de Snell:
$\displaystyle\frac{\sin\theta_2}{\sin\theta_1}=\displaystyle\frac{c_2}{c_1}$
onde $\theta$ é o ângulo de incidência entre a normal à superfície e o feixe, e $c$ são as velocidades do som nos meios 1 e 2. No caso de um feixe se propagando através da água do oceano, as velocidades mudam gradualmente. Por outro lado, é conveniente trabalhar com um ângulo $\vartheta$ do feixe em relação à horizontal. Portanto, a lei pode ser reescrita substituindo o seno do ângulo $\theta$ pelo cosseno do ângulo complementar $\vartheta$. Se considerarmos uma pequena variação do ângulo e da velocidade à medida que a profundidade aumenta em $dz$, obtemos:
$\displaystyle\frac{\cos(\vartheta + d\vartheta)}{\cos\vartheta}\sim 1-\tan\vartheta d\vartheta = 1+\displaystyle\frac{dc}{c}$
assim, a relação para a variação de profundidade é:
| $\displaystyle\frac{ d\vartheta }{ dz }=-\displaystyle\frac{\tan \vartheta }{ c } \displaystyle\frac{ dc }{ dz }$ |
ID:(11803, 0)