Utilisateur:
Propagation du son
Storyboard 
La propagation du son dans locéan prend en compte à la fois la réflexion à la surface et au fond de locéan, ainsi que les réfractions dues aux variations de pression, de température et de salinité.
ID:(1550, 0)
Propagation du son
Storyboard
La propagation du son dans locéan prend en compte à la fois la réflexion à la surface et au fond de locéan, ainsi que les réfractions dues aux variations de pression, de température et de salinité.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Exemples
Si l'on observe comment le son varie avec la profondeur et la mani re dont il se propage :
on peut voir que :
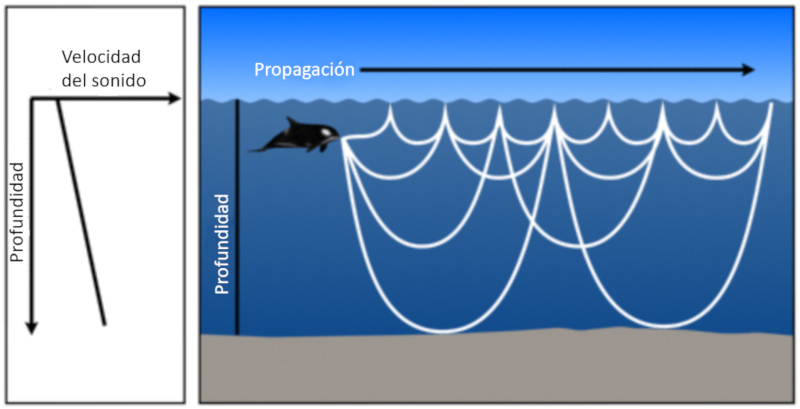
• Si la vitesse du son augmente avec la profondeur, l'angle entre le faisceau et l'horizon tend diminuer. Cela signifie que le son aura tendance r duire sa descente jusqu' devenir horizontal et, par sym trie, continuera monter vers la surface.
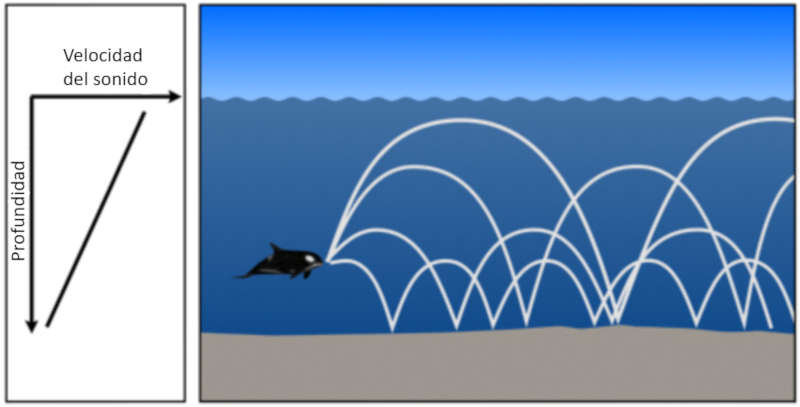
• Si la vitesse du son diminue avec la profondeur, l'angle entre le faisceau et l'horizon tend augmenter. Cela signifie que le son aura tendance augmenter sa descente vers le fond.
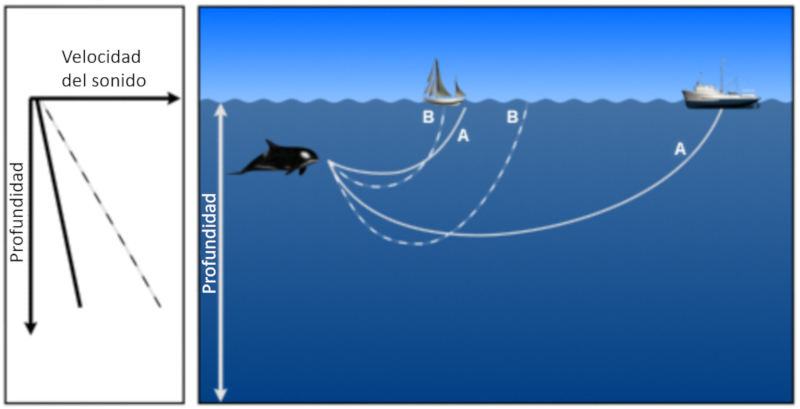
Son mis une profondeur dans laquelle la vitesse du son augmente avec la profondeur, les faisceaux finissent par revenir la surface o ils se r fl chissent et rep n tent le milieu :
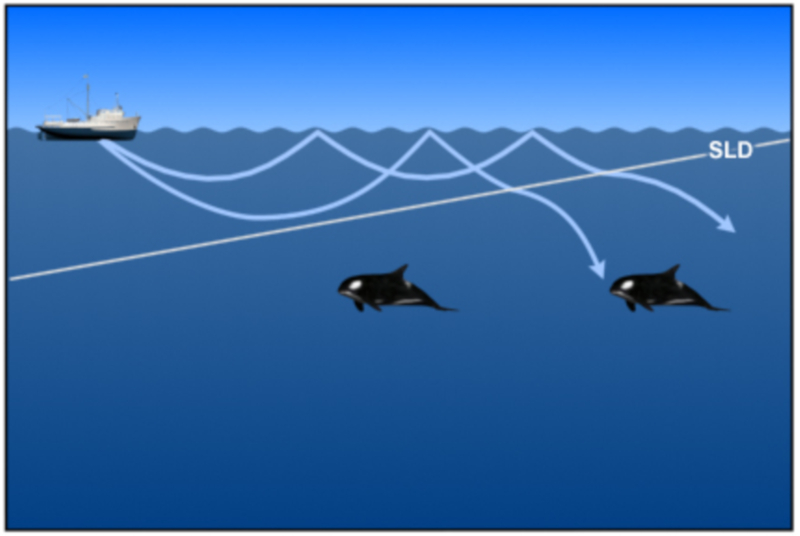
Le son mis une profondeur o la vitesse du son augmente avec la profondeur finit par revenir la surface. Cependant, si partir d'un point la vitesse du son diminue, on observe que les faisceaux avec un angle plus lev sont r fract s vers les profondeurs :
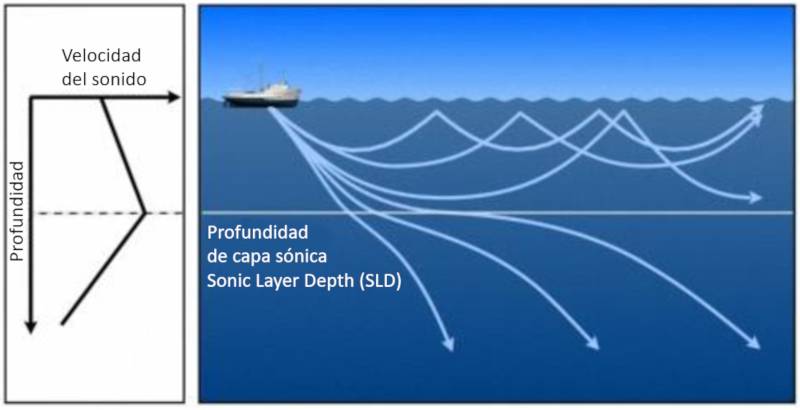
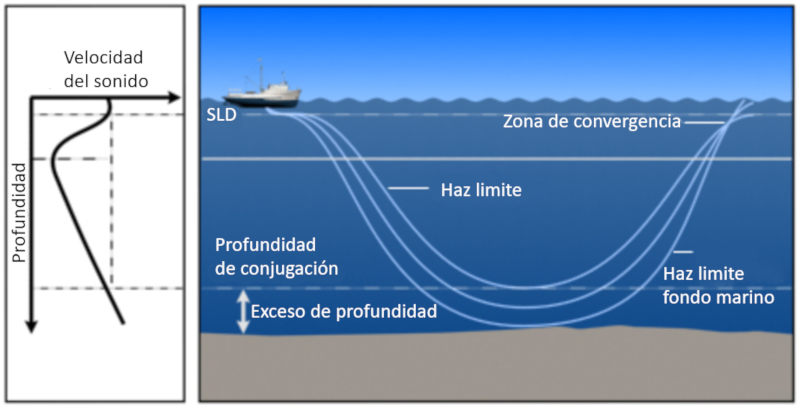
Ainsi, une zone se forme o les faisceaux reviennent la surface. Cette profondeur est appel e profondeur de la couche sonique (SLD) (Sonic Layer Depth).
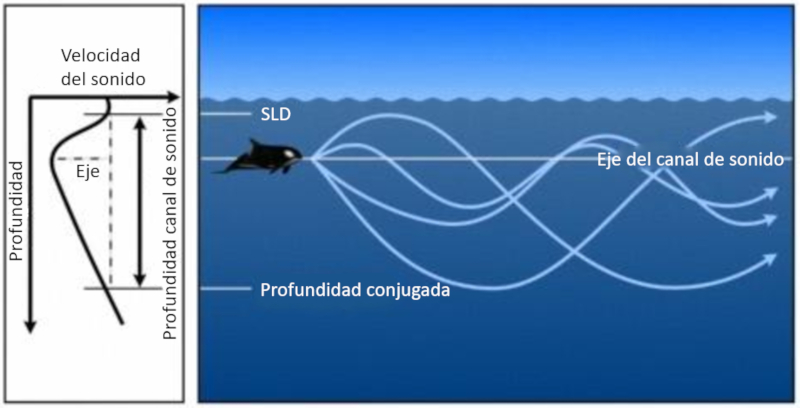
Lorsque le son diminue puis augmente nouveau, une zone se forme o il a tendance retourner vers la zone de vitesse minimale. Cette zone est appel e le canal sonore et s' tend de la profondeur de la couche sonique (SLD) une profondeur conjugu e :
La profondeur laquelle la vitesse du son atteint un minimum est appel e l'axe du canal sonore.
Il existe la fois une propagation dans la zone sup rieure la profondeur de la couche sonique (SLD) et dans le canal sonore. Cependant, la zone sup rieure pr sente le probl me que la surface att nue le son, rendant ainsi le canal sonore le plus efficace.
Les ondes sonores qui se propagent dans la profondeur de la couche sonique peuvent filtrer vers la zone inf rieure :
Si l'eau est peu profonde et que la vitesse du son ne fait qu'augmenter avec la profondeur, alors le son revient la surface soit par r fraction, soit par r flexion au fond, pour ensuite se refl ter la surface:
Si leau est peu profonde et que la vitesse du son ne diminue quavec la profondeur, le son a tendance aller vers le fond o il se refl te :
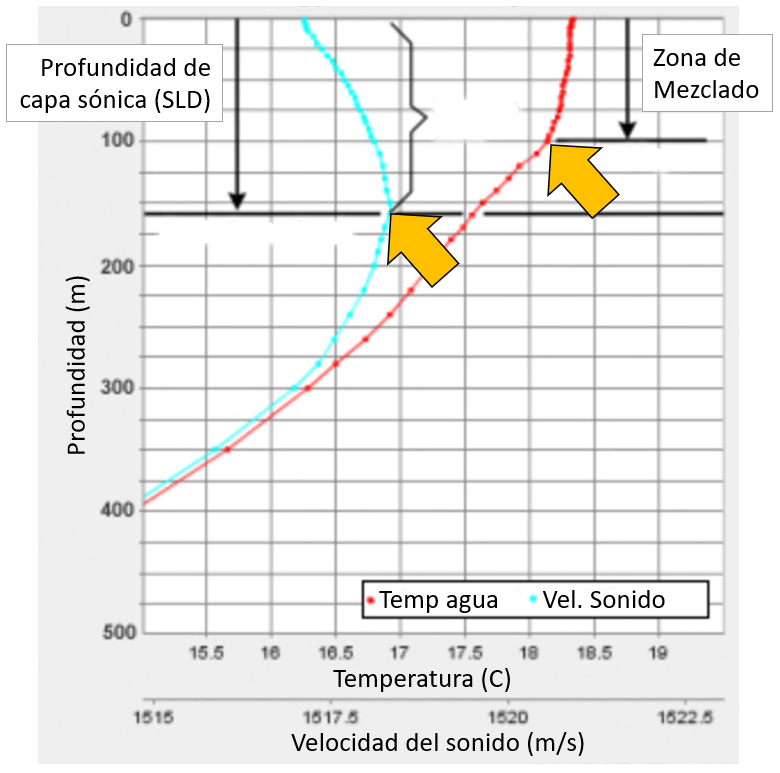
La temp rature traverse une zone o elle est approximativement constante avant de diminuer. Elle reste constante dans la premi re zone en raison des turbulences g n r es par le vent, qui ont tendance m langer l'eau.
La courbe de la vitesse du son montre qu'elle atteint un maximum qui d finit la profondeur de la couche sonique. son point maximum, la profondeur de la couche sonique est d finie :
En g n ral, en raison de la gravit , la vitesse du son augmente toujours avec la profondeur. Lorsqu'un faisceau sonore atteint la profondeur de la couche sonique SLD (sonic layer depth), il finit par se diverger et revenir la surface. Les faisceaux qui parviennent revenir la surface se situent entre une limite d finie par la r flexion au fond et la limite du faisceau qui parvient p n trer dans les couches inf rieures et atteint finalement la surface:
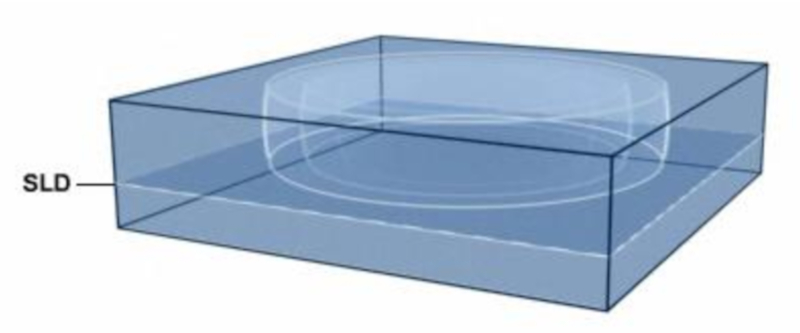
Pour le son mis pr s de la surface, la propagation peut tre mod lis e comme une propagation sph rique. Le son de haute fr quence a tendance s'amortir de plus grandes distances, donc le mod le sph rique est suffisant. Cependant, pour le son de basse fr quence, il peut voyager dans tout le bassin. Dans ce cas, il se d place travers la zone sup rieure jusqu' la profondeur de la couche acoustique (SLD) et/ou travers le canal sonore. Dans les deux cas, le syst me peut tre mod lis en utilisant des coordonn es cylindriques :
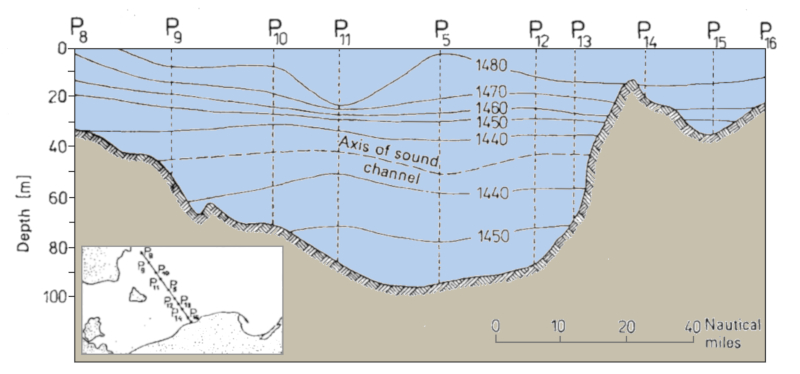
On peut obtenir un profil d'une zone, comme par exemple un canal, en repr sentant les vitesses pour chaque profondeur. Cela permet de d tecter les canaux sonores et la profondeur de la couche sonore :
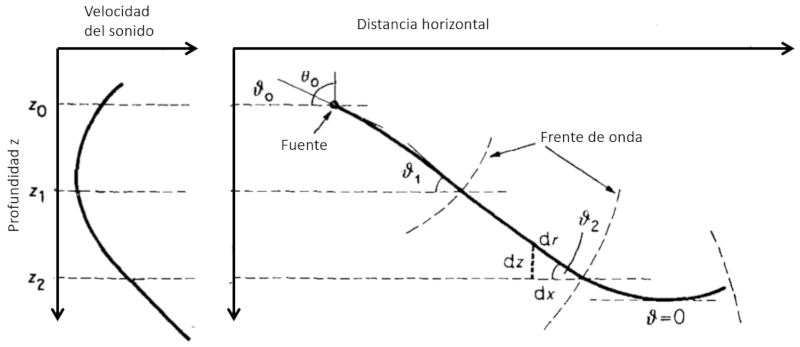
La r fraction du son lors du passage d'un milieu un autre est g n ralement d crite par la loi de Snell :
$\displaystyle\frac{\sin\theta_2}{\sin\theta_1}=\displaystyle\frac{c_2}{c_1}$
o $\theta$ est l'angle d'incidence entre la normale la surface et le faisceau, et $c$ sont les vitesses du son dans les milieux 1 et 2. Dans le cas d'un faisceau se propageant travers l'eau de l'oc an, les vitesses changent progressivement. D'autre part, il est pratique de travailler avec un angle $\vartheta$ du faisceau par rapport l'horizontale. Par cons quent, la loi peut tre r crite en rempla ant le sinus de l'angle $\theta$ par le cosinus de l'angle compl mentaire $\vartheta$. Si nous consid rons une petite variation de l'angle et de la vitesse mesure que la profondeur augmente de $dz$, nous avons :
$\displaystyle\frac{\cos(\vartheta + d\vartheta)}{\cos\vartheta}\sim 1-\tan\vartheta d\vartheta = 1+\displaystyle\frac{dc}{c}$
donc la relation pour la variation de profondeur est :
ID:(1550, 0)
