User:
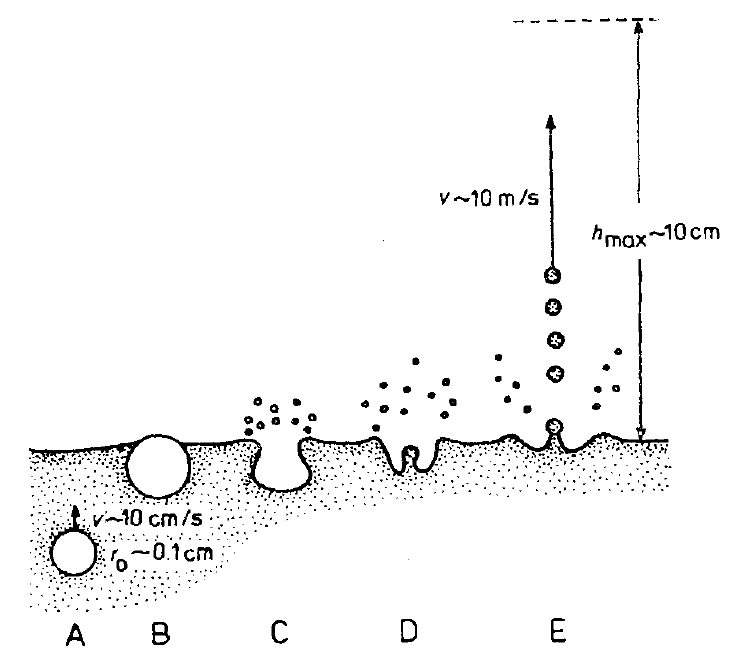
Acenso de burbujas a la superficie
Image 
Cuando ascienden burbujas a la superficie se observa que:
• la burbuja literalmente rompe la superficie que es generada por la tensión superficial
• al romper la superficie genera una serie de micro gotas que, por su tamaño, descienden muy lento hacia la superficie
• el fondo de la burbuja oscila generando a su vez un tipo de chorro que por la tensión superficial se corta formando gotas
Las gotas tienen bastante velocidad y por ello ascienden varios centímetros antes de volver a caer.
ID:(12246, 0)
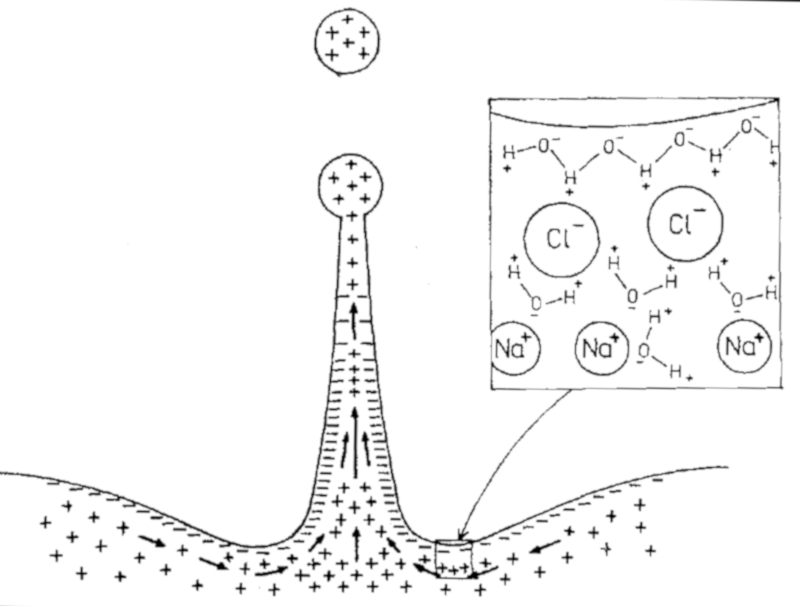
Cargas eléctricas
Image
Por la presencia de la sal en la superficie del océano se tienden a congregar cargas negativas relacionadas a los átomos e cloro.
La formación de gotas ocurre en el interior del agua donde predominan las cargas positivas y al ser disparada hacia la altura esta tipicamente cargada positivamente. Esto lleva a que se form un campo eléctrico entre la atmósfera sobre el océano y la superficie de de este.
ID:(12247, 0)
Langmuir Number
Equation
The Langmuir number examines the relationship between the atmospheric velocity associated with interaction (friction) and the Stokes surface velocity. Therefore, the Langmuir number can be defined as the ratio of the square root of both velocities:
 $ La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}$ |
ID:(12219, 0)
Langmuir stable waves
Description
In the attached work accompanying the image, the stability ranges of flows forming Langmuir circulations are studied under the linear approximation. Different zones are presented, depicting the relationship between the Langmuir number and the wave vector when the Richardson number is zero.
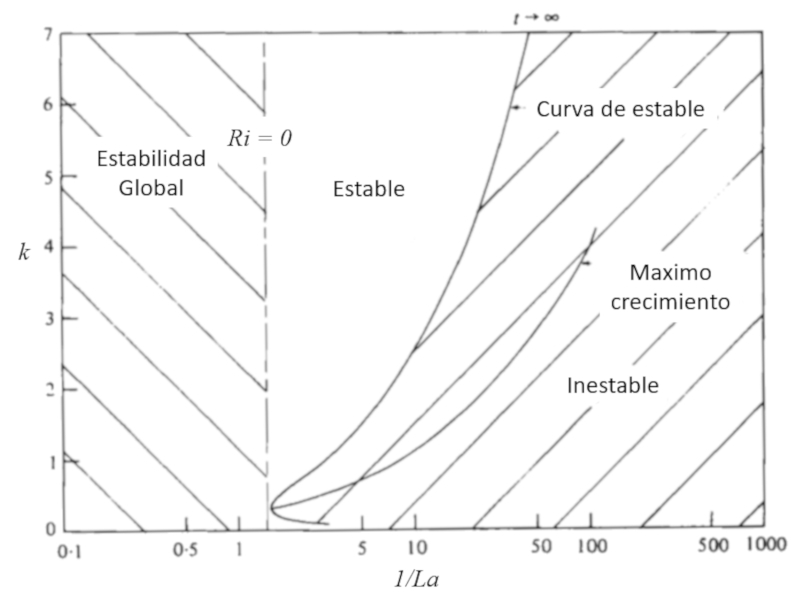
The instability of the ocean to Langmuir circulations, S. Leibovich and S. Paoluccit, J. Fluid Mech. (1981). vol. 102, pp. 141-167
ID:(12221, 0)
Wave description
Equation
A wave can be approximated by a sinusoid in terms of position $x$ and time $t$.
The function includes the amplitude $z$ at each point, the maximum amplitude $z_0$, the wave vector $k$, and the angular frequency $\omega$:
| $ z ( x , t ) = z_0 sin( k x - \omega t )$ |
ID:(12307, 0)
Wave vector
Equation
The wave vector is the factor that multiplies the position and corresponds to the value for which if the wave is shifted by one wavelength, it assumes the same shape as it had initially. To achieve this, it is necessary that:
$kx = k\lambda = 2\pi$
Therefore, with the wavelength $\lambda$, we have:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(12309, 0)
Frecuencia angular
Equation
Si se recuerda que la velocidad angular era el angulo recorrido en el tiempo se puede ver que la expresión\\n\\n
$\displaystyle\frac{2\pi}{T}$
corresponde a una vuelta completa (
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(12335, 0)
Wave phase velocity
Equation
Waves have a velocity that depends on the water depth and the wave vector $k$, which can be calculated using the wavelength $\lambda$ as:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
In the case of the phase velocity, which is the velocity at which each wave crest moves, it can be determined using the water depth $h$ and the gravitational acceleration $g$. The phase velocity is given by:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
The phase velocity corresponds to the speed at which a particular oscillation or wave propagates.
ID:(12305, 0)
Wave group velocity
Equation
Waves have a velocity that depends on the water depth and the wave vector $k$, which can be calculated using the wavelength $\lambda$ as:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
In the case of the group velocity, which is the velocity at which the wave train moves as a whole and not each individual wave, it can be calculated based on the phase velocity $c_p$, which is determined by the water depth $h$ and the gravitational acceleration $g$, as:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
Finally, with this velocity, the group velocity can be calculated using the following expression:
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
The group velocity is the velocity at which the wave train or group of waves travels through the medium.
ID:(12304, 0)
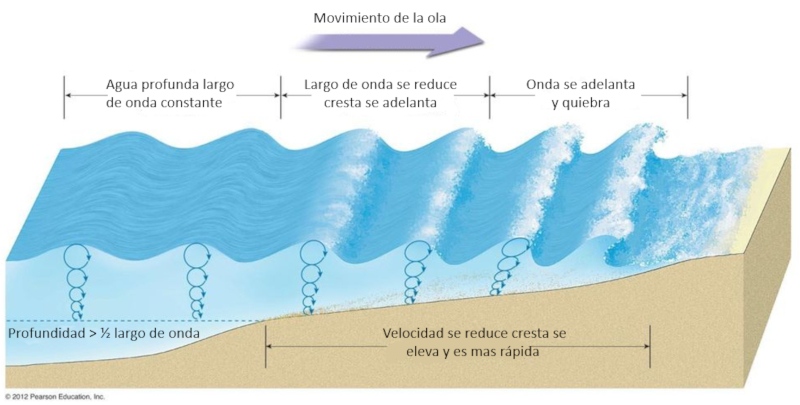
Break of the wave on the beach
Description
When a wave reaches the shore, it starts to climb up the beach slope, becoming progressively shallower and slower. A following wave tends to rise over the preceding wave. As the water becomes deeper in this situation, it becomes faster and tends to overtake the previously arrived water. This interaction ultimately leads to the wave breaking, creating the phenomenon known as surf.
ID:(12308, 0)