Usuario:


Balance de Masas
Storyboard

>Modelo

ID:(1307, 0)


Profundidad del Glaciar
Definición

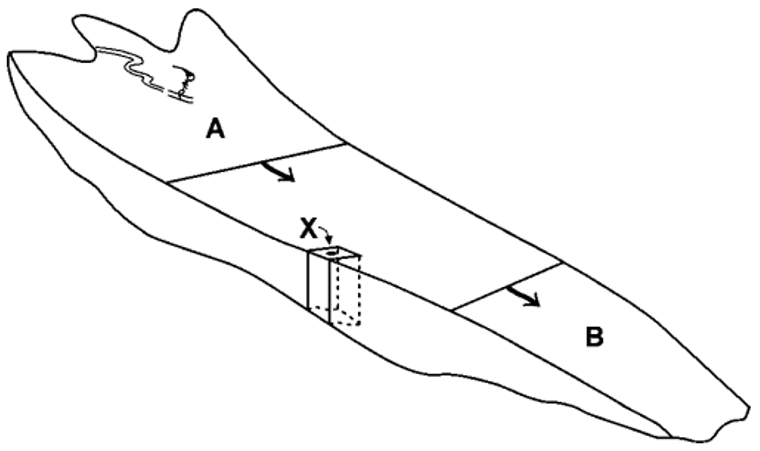
Para estudiar el estado de un glaciar se puede medir la profundidad en toda la superficie del glaciar:

ID:(9958, 0)


Estructura del cambio de masa
Imagen

La variación de la masa en el tiempo solo nos entrega la información de como evoluciona la masa del hielo. Sin embargo se puede caracterizar mejor el Glaciar estudiando como este en sectores crece mientras que en otros decrece.

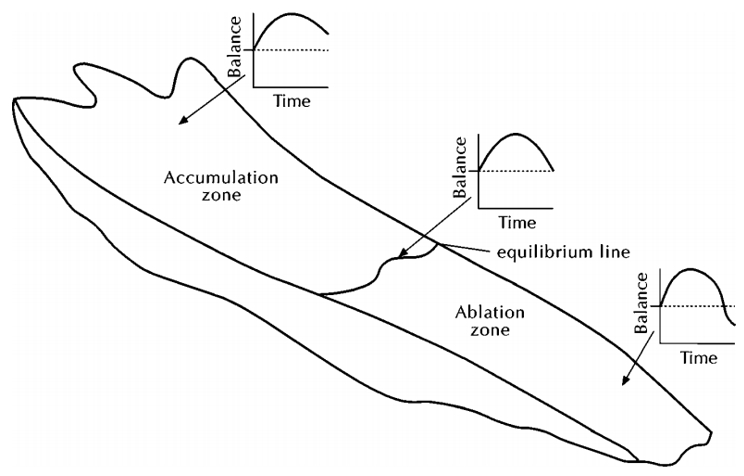
Si se observan las lineas de altura se puede encontrar una tal que separa una zona en que aumenta el volumen de una que presenta el mismo volumen como perdida:

ID:(9961, 0)


Balance de Masas
Descripción

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$l$
l
Calor latente específico del hielo
J/kg
$\lambda$
lam
Conductividad del hielo
W/m K
$\rho_w$
rho_w
Densidad del agua
kg/m^3
$\rho_i$
rho_i
Densidad del hielo del glaciar
kg/m^3
$h$
h
Grosor del glaciar
m
$I$
I
Intensidad por calor conducido
W/m^2
$I_d$
I_d
Intensidad por calor de deformación
W/m^2
$I_f$
I_f
Intensidad por calor de roce
W/m^2
$I_{gs}$
I_gs
Intensidad por calor en superficie
W/m^2
$T_c$
T_c
Temperatura en el centro del glaciar
K
$T_{be}$
T_be
Temperatura en la base del glaciar
K
$T_{ge}$
T_ge
Temperatura en la superficie del glaciar
K
$b_z$
b_z
Velocidad de ablación del glaciar
m/s
$b_b$
b_b
Velocidad de ablación en base
m/s
$b_i$
b_i
Velocidad de ablación en interior
m/s
$b_s$
b_s
Velocidad de ablación en superficie
m/s
$b_w$
b_w
Velocidad de ablación equivalente en agua
m/s
$a_i$
a_i
Velocidad de acumulación
m/s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Para estudiar el estado de un glaciar se puede medir la profundidad en toda la superficie del glaciar:

(ID 9958)

El deshielo y consecuente perdida de grosor del glaciar ocurre en la medida que el calor generado es mayor que el eliminado por conducci n quedando una calor por tiempo

\Delta I,dS,dt

donde \Delta I es el remanente de intensidad, dS la secci n y dt el tiempo transcurrido.

La energ a sobrante es capaz de calentar y descongelar un volumen dS dz donde dz es la altura. Si \rho_i es la densidad del hielo, c es el calor especifico, \Delta T la diferencia de la temperatura con respecto de su temperatura de fusi n y L es el calor latente, entonces se tiene que por conservaci n de energ a:

\Delta I,dS,dt=(L,+c,\Delta T)\rho_i,dS,dz

Como el calor latente L es mucho mayor que el calor espec fico multiplicado por la diferencia de temperatura c,\Delta T y con la velocidad de descongelar

b_z\equiv\displaystyle\frac{dz}{dt}

ser

(ID 10000)

El derretimiento ocurre en funci n de que el calor generado es mayor que aquel perdido por la conducci n quedando un resto que calienta y eventualmente derrite parte del hielo. El derretimiento conlleva a la reducci n de la altura del glaciar a una velocidad



En el caso de la superficie el flujo de energ a en la superficie

$I_{gs}=(1-\gamma_v)(1-a_{ge})I_s+\sigma\epsilon(T_{ge}^4-T_b^4)-(\kappa_l+\kappa_c(T_{ge}-T_t))u$



supera la conducci n correspondiente

$I=\lambda\displaystyle\frac{\Delta T}{\Delta h}$



se tendr que si se supone la temperatura en el centro del glaciar es T_c, en la superficie T_{ge} y se asume que la profundidad total es h se tiene una velocidad de deshielo de

$b_s=\displaystyle\frac{1}{l\rho_i}\left(I_{gs}-\displaystyle\frac{2\lambda (T_{ge}-T_c)}{h}\right)$

donde \theta(x) denota la funci n de heavyside que es igual a su argumento si este es positivo y cero si es negativo.

(ID 9996)

El derretimiento ocurre en funci n de que el calor generado es mayor que aquel perdido por la conducci n quedando un resto que calienta y eventualmente derrite parte del hielo. El derretimiento conlleva a la reducci n de la altura del glaciar a una velocidad



En el caso del interior el flujo ser

$I_d = \displaystyle\frac{1}{(n_g+1)\tau_g}\displaystyle\frac{(\rho_i\,g\,h\,\sin\theta )^{n_g+1}}{\sigma_g^{n_g}}$



supera la conducci n correspondiente

$I=\lambda\displaystyle\frac{\Delta T}{\Delta h}$



se tendr una reducci n de la profundidad del glaciar seg n

$b_i=\displaystyle\frac{1}{l\rho_i}\left(I_d+\displaystyle\frac{2\lambda (T_{be}+T_{ge}-2T_c}{h}\right)$

(ID 9997)

El derretimiento ocurre en funci n de que el calor generado es mayor que aquel perdido por la conducci n quedando un resto que calienta y eventualmente derrite parte del hielo. El derretimiento conlleva a la reducci n de la altura del glaciar a una velocidad



En el caso de la base el flujo de energ a es

$I_f=\sigma_bv_b$



supera la conducci n correspondiente

$I=\lambda\displaystyle\frac{\Delta T}{\Delta h}$



se tendr que si se supone la temperatura en el centro del glaciar es T_c, en la superficie T_{gb} y se asume que la profundidad total es h se tiene una velocidad de deshielo de

$b_b=\displaystyle\frac{1}{l\rho_i}\left(I_f-\displaystyle\frac{2\lambda (T_{be}-T_c}{h}\right)$

donde \theta(x) denota la funci n de heavyside que es igual a su argumento si este es positivo y cero si es negativo.

(ID 9998)

El cambio de grosor en un punto se puede calcular con la suma de las velocidades de los derretimientos de superficie,

$b_s=\displaystyle\frac{1}{l\rho_i}\left(I_{gs}-\displaystyle\frac{2\lambda (T_{ge}-T_c)}{h}\right)$



interior

$b_i=\displaystyle\frac{1}{l\rho_i}\left(I_d+\displaystyle\frac{2\lambda (T_{be}+T_{ge}-2T_c}{h}\right)$



y base

$b_b=\displaystyle\frac{1}{l\rho_i}\left(I_f-\displaystyle\frac{2\lambda (T_{be}-T_c}{h}\right)$



restando lo que se acumula por nieve caida a_i

$b=b_s+b_i+b_b-a_i$

(ID 10001)

Si se multiplica el balance especifico b por un elemento de superficie dS se obtienen la masa en el rea

b,dS

por lo que la suma sobre toda la superficie nos entrega la masa:

$M=\displaystyle\int_S b\,dS$

(ID 9960)

La variaci n de la masa en el tiempo solo nos entrega la informaci n de como evoluciona la masa del hielo. Sin embargo se puede caracterizar mejor el Glaciar estudiando como este en sectores crece mientras que en otros decrece.

Si se observan las lineas de altura se puede encontrar una tal que separa una zona en que aumenta el volumen de una que presenta el mismo volumen como perdida:

(ID 9961)

Como el glaciar puede contener agua se puede introducir un balance equivalente de hielo en equivalente en agua. Para ello basta igualar la masas de hielo (i, ice) con el del agua (w, water). Si se tiene un balance equivalente en hielo b_i con la densidad del hielo \rho_i y la profundidad del agua b_w con la densidad del agua \rho_w:

\rho_ib_i=\rho_wb_w

por lo que se tiene la profundidad equivalente:

$b_w=\displaystyle\frac{\rho_i}{\rho_w}b_i$

(ID 9959)

ID:(1307, 0)