Storyboard

Una aplicación es el estudio de los datos de los pasajeros del Titanic y la probabilidad de sobre-vivencia según sus características. En este caso se usa un modelo lineal para el estimador de clasificaciones.

Código y datos

LinearTitanic.ipynb

titanic_lin_train.csv

titanic_lin_eval.csv

>Modelo

ID:(1790, 0)

Descripción

>Top

Setup para modelo lineal:

import os
import sys

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import clear_output
from six.moves import urllib

ID:(13828, 0)

Descripción

>Top

Cargar los datos de los pasajeros del viaje inaugural del Titanic.

import tensorflow.compat.v2.feature_column as fc
import tensorflow as tf

# Load dataset.
dftrain = pd.read_csv('titanic_lin_train.csv')
dfeval = pd.read_csv('titanic_lin_eval.csv')
dftest = pd.read_csv('titanic_lin_test.csv')
y_train = dftrain.pop('survived')
y_eval = dfeval.pop('survived')

ID:(13829, 0)

Descripción

>Top

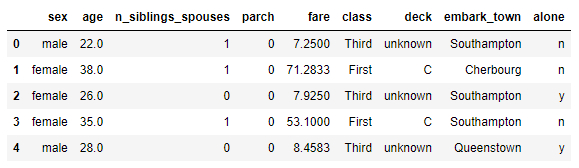
Mostrar estructuras y datos del conjunto de datos de los pasajeros del Titanic:

# show structure and data
dftrain.head()

ID:(13830, 0)

Descripción

>Top

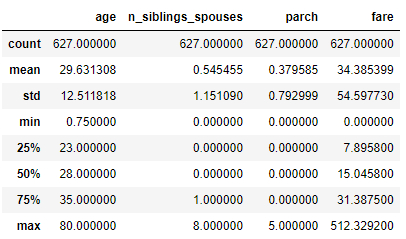
Mostrar estadística de datos de los pasajeros del Titanic

# show statistics of data
dftrain.describe()

ID:(13831, 0)

Descripción

>Top

Número de registros para entrenar y evaluar:

# number of train and evaluation records
dftrain.shape[0], dfeval.shape[0]

(627, 264)

ID:(13832, 0)

Descripción

>Top

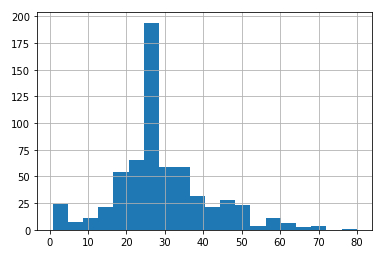
Para mostrar el histograma (vertical) hist de las edades dftrain.age con intervalo de 20 años (bins=20) se obtiene de

# age histogram
dftrain.age.hist(bins=20)

ID:(13833, 0)

Descripción

>Top

Para mostrar el histograma (horizontal) plot(kind='barh') del genero dftrain.sex contando el numero de pasajeros según genero value_counts() se obtiene

# gender histogram
dftrain.sex.value_counts().plot(kind='barh')

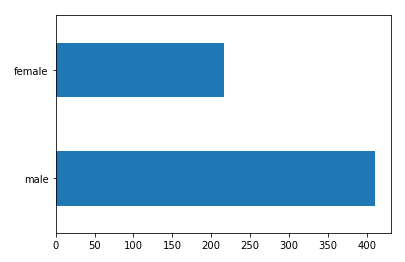
ID:(13834, 0)

Descripción

>Top

Para mostrar el histograma (horizontal) plot(kind='barh') de las classes dftrain['class'] contando el numero de pasajeros según clase value_counts() se obtiene

# class histogram
dftrain['class'].value_counts().plot(kind='barh')

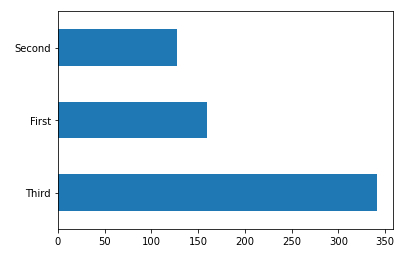
ID:(13835, 0)

Descripción

>Top

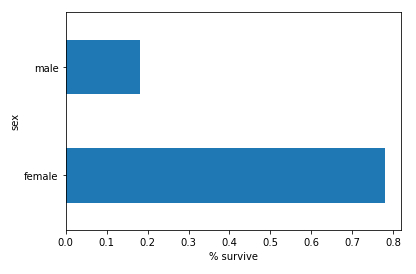
Para mostrar el histograma (horizontal) plot(kind='barh') de los sobrevivientes survived promediado mean() agrupados por genero groupby('sex') con la etiqueta en el eje x set_xlabel('% survive') de la serie armada por concadenar pd.concat([dftrain,y_train],axis=1) de todos los datos dftrain y la abscisa y_train;

# survived histogram
pd.concat([dftrain, y_train], axis=1).groupby('sex').survived.mean().plot(kind='barh').set_xlabel('% survive')

ID:(13836, 0)

Descripción

>Top

Para formar el tensor de los datos feature_columns se deben sumarse según sean de categorías o numéricas.
Las primeras se rescatan vía el arreglo vocabulary y se agregan con el comando append formando la columna con el comando tf.feature_column.categorical_column_with_vocabulary_list.
Las segundas se asignan en forma directa con el comando append con la columna via su designación tf.feature_column.numeric_column.

# define tensor
feature_columns = []

# define categorical columns names
CATEGORICAL_COLUMNS = ['sex', 'class', 'deck', 'embark_town', 'alone']
# build columns of categorical variables
for feature_name in CATEGORICAL_COLUMNS:
  vocabulary = dftrain[feature_name].unique()
  feature_columns.append(tf.feature_column.categorical_column_with_vocabulary_list(feature_name, vocabulary))

# define numeric columns names
FLOAT_COLUMNS = ['age', 'fare']
# build columns of numeric variables
for feature_name in FLOAT_COLUMNS:
  feature_columns.append(tf.feature_column.numeric_column(feature_name, dtype=tf.float32))

# define numeric columns names
NUMERIC_COLUMNS = ['n_siblings_spouses', 'parch']
# build columns of numeric variables
for feature_name in NUMERIC_COLUMNS:
  feature_columns.append(tf.feature_column.numeric_column(feature_name, dtype=tf.int32))

ID:(13837, 0)

Descripción

>Top

Se define una función para generar arreglos para los procesos de entrenamiento y evaluación:

# define function for making set
def make_input_fn(data_df, label_df, num_epochs=10, shuffle=True, batch_size=32):
  def input_function():
    ds = tf.data.Dataset.from_tensor_slices((dict(data_df), label_df))
    if shuffle:
      ds = ds.shuffle(1000)
    ds = ds.batch(batch_size).repeat(num_epochs)
    return ds
  return input_function

# generate training input
train_input_fn = make_input_fn(dftrain, y_train)
# generate evaluating input
eval_input_fn = make_input_fn(dfeval, y_eval, num_epochs=1, shuffle=False)

ID:(13838, 0)

Descripción

>Top

Para realizar la clasificación se define el modelo mediante la función estimator.LinearClassifier aplicado sobre las columnas de los datos feature_columns.

# define model
linear_model = tf.estimator.LinearClassifier(feature_columns=feature_columns)

# define train model
linear_model.train(train_input_fn)

# evaluate model
result = linear_model.evaluate(eval_input_fn)

# print result
clear_output()
print(result)

Se obtiene:

{'accuracy': 0.75757575, 'accuracy_baseline': 0.625, 'auc': 0.83067036, 'auc_precision_recall': 0.78773487, 'average_loss': 0.49594572, 'label/mean': 0.375, 'loss': 0.49112648, 'precision': 0.65217394, 'prediction/mean': 0.44832677, 'recall': 0.75757575, 'global_step': 200}

ID:(13841, 0)

Descripción

>Top

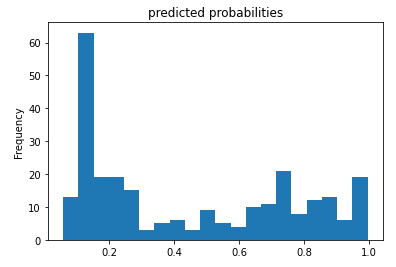
Si se evalúa la probabilidad de sobre-vivencia pronosticada en función de su frecuencia:

# histogram of the probability
pred_dicts = list(linear_est.predict(eval_input_fn))
probs = pd.Series([pred['probabilities'][1] for pred in pred_dicts])

probs.plot(kind='hist', bins=20, title='predicted probabilities')

ID:(13839, 0)

Descripción

>Top

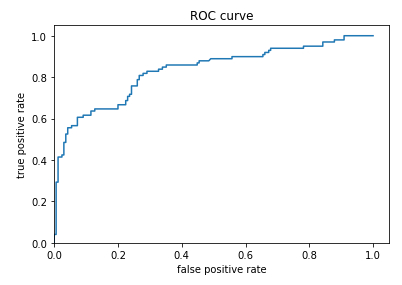
Para usar este pronostico se debe definir un valor limite de la propiedad para definir sobre que valor se va a pronosticar que se sobrevive y bajo la cual se pronosticara la no sobre-vivencia. Para ello se debe evaluar la probabilidad de que se pronostique la sobre-vivencia y se observe esta (true positive) y compararla con la probabilidad que de pronostique la sobre-vivencia cuando no se sobrevive (false positive).\\nEl factor true-positive TPR o sensitividad se define como\\n\\n

$TPR=\displaystyle\frac{TP}{TP+FN}$

\\n\\ndonde true-positive TP los casos pronosticados correctamente como positivos y los false-negative FN que corresponden a los casos pronosticados como negativos que resultan negativos.\\nEl factor false-positive FPR se define como\\n\\n

$FPR=\displaystyle\frac{FP}{FP+TN}$

donde false-positive FP los casos pronosticados como positivos cuando es en realidad falso y los false-negative FN que corresponden a los casos pronosticados como negativos que resultan negativos.

from sklearn.metrics import roc_curve
from matplotlib import pyplot as plt

fpr, tpr, _ = roc_curve(y_eval, probs)
plt.plot(fpr, tpr)
plt.title('ROC curve')
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.xlim(0,)
plt.ylim(0,)

ID:(13840, 0)