Lineares Modell mit Schätzer erstellen (Titanic-Dataset)
Storyboard 
Eine Anwendung ist die Untersuchung der Daten der Passagiere der Titanic und der Überlebenswahrscheinlichkeit nach ihren Eigenschaften. In diesem Fall wird für den Ranking-Schätzer ein lineares Modell verwendet.
Code und Daten
ID:(1790, 0)
Setup für lineares Modell
Beschreibung 
Setup für lineares Modell:
import os import sys import numpy as np import pandas as pd import matplotlib.pyplot as plt from IPython.display import clear_output from six.moves import urllib
ID:(13828, 0)
Datensatz laden
Beschreibung 
Passagierdaten für die Jungfernfahrt der Titanic laden:
import tensorflow.compat.v2.feature_column as fc
import tensorflow as tf
# Load dataset.
dftrain = pd.read_csv('titanic_lin_train.csv')
dfeval = pd.read_csv('titanic_lin_eval.csv')
dftest = pd.read_csv('titanic_lin_test.csv')
y_train = dftrain.pop('survived')
y_eval = dfeval.pop('survived')
ID:(13829, 0)
Strukturen und Daten
Beschreibung 
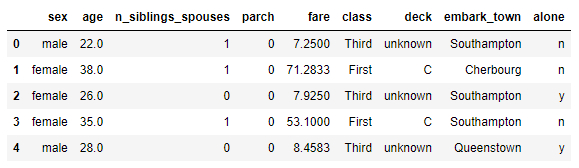
Strukturen und Daten aus dem Titanic-Passagierdatensatz anzeigen:
# show structure and data dftrain.head()
ID:(13830, 0)
Datenstatistik anzeigen
Beschreibung 
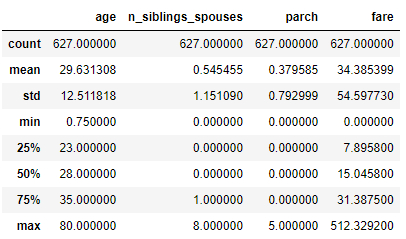
Titanic-Passagierdatenstatistik anzeigen
# show statistics of data dftrain.describe()
ID:(13831, 0)
Anzahl zu trainierender und auszuwertender Datensätze
Beschreibung 
Anzahl zu trainierender und auszuwertender Datensätze:
# number of train and evaluation records dftrain.shape[0], dfeval.shape[0]
(627, 264)
ID:(13832, 0)
Histogramm (vertikal) des Alters anzuzeigen
Beschreibung 
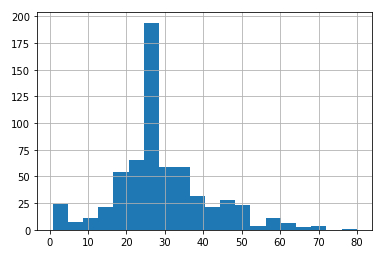
Um das Histogramm (vertikal) anzuzeigen, wird hist des Alters dftrain.age mit einem Intervall von 20 Jahren (bins = 20) erhalten aus
# age histogram dftrain.age.hist(bins=20)
ID:(13833, 0)
Histogramm (horizontal) des Geschlechts anzuzeigen
Beschreibung 
Anzeige des Histogramms (horizontal) Plot (kind = 'barh') des Genres dftrain.sex Zählung der Passagiere nach Genre value_counts () < / b > du bekommst# gender histogram
dftrain.sex.value_counts().plot(kind='barh')
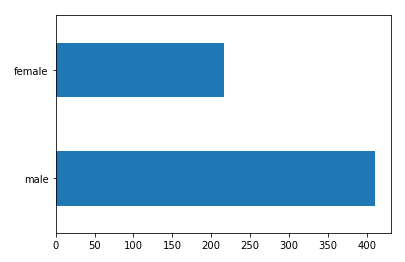
ID:(13834, 0)
Histogramm (horizontal) der Klassen anzuzeigen
Beschreibung 
Anzeige des Histogramms (horizontal) plot (kind='barh') der Klassen dftrain['class'] Zählung der Passagiere nach Klassen value_counts() du bekommst
# class histogram dftrain['class'].value_counts().plot(kind='barh')
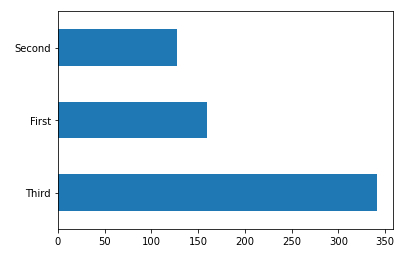
ID:(13835, 0)
Histogramm (horizontal) der Klassen anzuzeigen
Beschreibung 
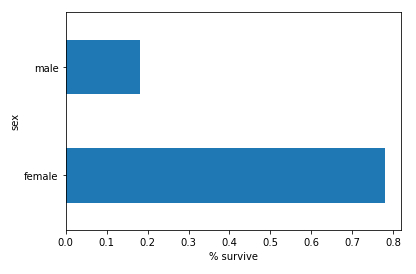
Zur Anzeige des Histogramms (horizontal) plot(kind='barh')der Überlebendensurvived gemittelt mean() gruppiert nach Geschlecht groupby('sex') mit dem set_xlabel('% survive')x-Achsen-Label des Strings, der durch Verkettung vonpd.concat([dftrain,y_train],axis=1) aller Daten dftrain und der Abszisse y_train;
# survived histogram
pd.concat([dftrain, y_train], axis=1).groupby('sex').survived.mean().plot(kind='barh').set_xlabel('% survive')
ID:(13836, 0)
Datenspalten bilden
Beschreibung 
Um den Tensor zu bilden, müssen die feature_columns Daten hinzugefügt werden, je nachdem, ob es sich um Kategorien oder Zahlen handelt.
Erstere werden über das Array vokabular gerettet und mit dem Befehl append hinzugefügt, wodurch die Spalte mit dem Befehl tf.feature_column.categorical_column_with_vocabulary_list gebildet wird.
Letztere werden mit dem Befehl append direkt mit der Spalte über ihre Bezeichnung tf.feature_column.numeric_column belegt.
# define tensor feature_columns = [] # define categorical columns names CATEGORICAL_COLUMNS = ['sex', 'class', 'deck', 'embark_town', 'alone'] # build columns of categorical variables for feature_name in CATEGORICAL_COLUMNS: vocabulary = dftrain[feature_name].unique() feature_columns.append(tf.feature_column.categorical_column_with_vocabulary_list(feature_name, vocabulary)) # define numeric columns names FLOAT_COLUMNS = ['age', 'fare'] # build columns of numeric variables for feature_name in FLOAT_COLUMNS: feature_columns.append(tf.feature_column.numeric_column(feature_name, dtype=tf.float32)) # define numeric columns names NUMERIC_COLUMNS = ['n_siblings_spouses', 'parch'] # build columns of numeric variables for feature_name in NUMERIC_COLUMNS: feature_columns.append(tf.feature_column.numeric_column(feature_name, dtype=tf.int32))
ID:(13837, 0)
Formular zum Trainieren und Auswerten eingestellt
Beschreibung 
Es wird eine Funktion definiert, um Regelungen für die Trainings- und Bewertungsprozesse zu generieren:
# define function for making set
def make_input_fn(data_df, label_df, num_epochs=10, shuffle=True, batch_size=32):
def input_function():
ds = tf.data.Dataset.from_tensor_slices((dict(data_df), label_df))
if shuffle:
ds = ds.shuffle(1000)
ds = ds.batch(batch_size).repeat(num_epochs)
return ds
return input_functionGenerierung von Sets für Training und Auswertung:
# generate training input train_input_fn = make_input_fn(dftrain, y_train) # generate evaluating input eval_input_fn = make_input_fn(dfeval, y_eval, num_epochs=1, shuffle=False)
ID:(13838, 0)
Training und Auswertung
Beschreibung 
Um die Klassifizierung durchzuführen, wird das Modell mithilfe der Funktion estimator.LinearClassifier definiert, die auf die Spalten der feature_columns-Daten angewendet wird.
# define model linear_model = tf.estimator.LinearClassifier(feature_columns=feature_columns)
Dann trainieren wir das Modell, indem wir trainieren auf das Modell anwenden linear_model mit den Daten, um train_input_fn zu trainieren
# define train model linear_model.train(train_input_fn)
Schließlich wird es mit evaluieren auf das Modell angewendet linear_model und den zu evaluierenden Daten eval_input_fn . ausgewertet
# evaluate model result = linear_model.evaluate(eval_input_fn)
El resultado final se imprime en mediante el comando print:
# print result clear_output() print(result)
Wird erhalten:
{'accuracy': 0.75757575, 'accuracy_baseline': 0.625, 'auc': 0.83067036, 'auc_precision_recall': 0.78773487, 'average_loss': 0.49594572, 'label/mean': 0.375, 'loss': 0.49112648, 'precision': 0.65217394, 'prediction/mean': 0.44832677, 'recall': 0.75757575, 'global_step': 200}
ID:(13841, 0)
Histogramm der Überlebenswahrscheinlichkeiten
Beschreibung 
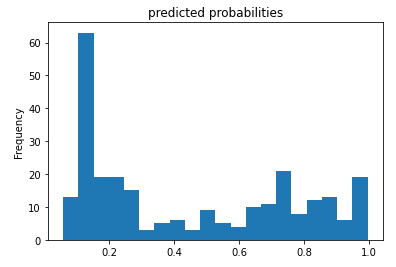
Wenn die vorhergesagte Überlebenswahrscheinlichkeit anhand ihrer Häufigkeit bewertet wird:
# histogram of the probability pred_dicts = list(linear_est.predict(eval_input_fn)) probs = pd.Series([pred['probabilities'][1] for pred in pred_dicts]) probs.plot(kind='hist', bins=20, title='predicted probabilities')
Sie erhalten eine Verteilung des Formulars:
ID:(13839, 0)
ROC Kurve
Beschreibung 
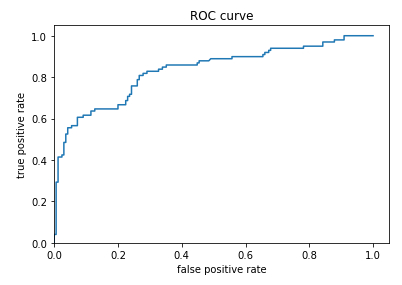
Um diese Prognose zu verwenden, muss ein Grenzwert der Immobilie definiert werden, um zu definieren, bei welchem ??Wert das Überleben vorhergesagt wird und unter welchem ??das Nicht-Überleben vorhergesagt wird. Dazu muss die Wahrscheinlichkeit, dass das Überleben vorhergesagt und beobachtet wird (richtig positiv) bewertet und mit der Wahrscheinlichkeit verglichen wird, dass das Überleben vorhergesagt wird, wenn es nicht überlebt wird (falsch positiv).\\nDer wahr-positive
$TPR=\displaystyle\frac{TP}{TP+FN}$
\\n\\nwobei wahr-positiv
$FPR=\displaystyle\frac{FP}{FP+TN}$
wobei falsch-positiv
from sklearn.metrics import roc_curve
from matplotlib import pyplot as plt
fpr, tpr, _ = roc_curve(y_eval, probs)
plt.plot(fpr, tpr)
plt.title('ROC curve')
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.xlim(0,)
plt.ylim(0,)Die Darstellung beider Wahrscheinlichkeiten wird als ROC-Diagramm (Receiver Operating Characteristic) bezeichnet:
ID:(13840, 0)
