Solar radiation
Storyboard
The origin of the weather is the sun. Its energy reaches the earth by heating in a different way atmosphere and surface creating gradients that are balanced by conduction, convection and winds.
Therefore, the power of the sun must be studied, how it reaches the earth and how it is distributed over the earth's surface.
ID:(534, 0)
The sun
Description
The source of energy that defines the Earth's climate is the sun.

The key parameters of the sun are:
Parameter | Variable | Value
|:-------------|:------------|:--------:
Radius | $R$ | $696,342 km$
Surface Area | $S$ | $6.09 \times 10^{12} km^2$
Mass | $M$ | $1.98855 \times 10^{30} kg$
Density | $\rho$ | $1.408 g/cm^2$
Surface Temperature | $T_s$ | $5778 K$
Power | $P$ | $3.846 \times 10^{26} W$
Intensity | $I$ | $6.24 \times 10^7 W/m^2$
ID:(3078, 0)
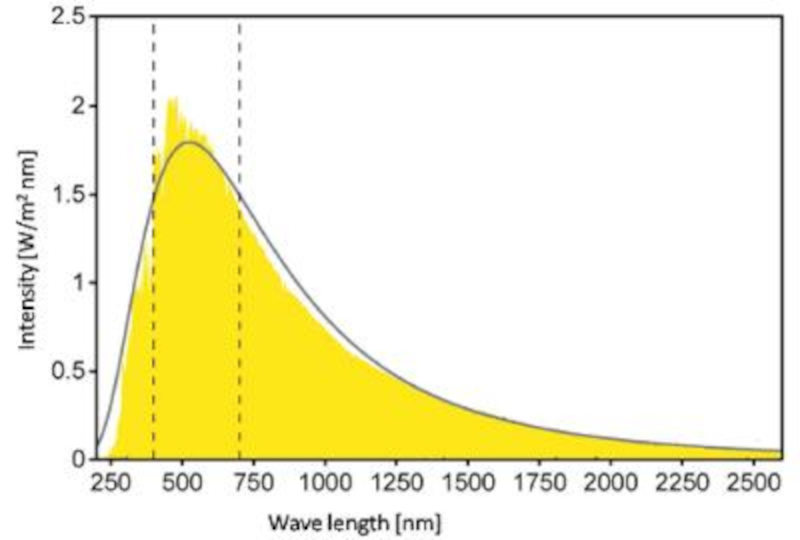
Spectrum of the sun
Description
The Sun emits radiation with a spectrum similar to what is known as the blackbody spectrum. Its maximum irradiation occurs at a wavelength close to the color yellow:
None
ID:(3083, 0)
Intensity and power
Equation
The intensity $I$ is defined as the power $P$ per unit surface area $S$ that is radiated. Therefore, we have the following relationship:
ID:(9988, 0)
Sun power
Equation
The intensity is defined as power per unit area, where power is represented by
| $ I =\displaystyle\frac{ P }{ S }$ |
If we model the Sun as a sphere, its surface area is
| $ S = 4 \pi R ^2$ |
and thus the intensity is calculated as
.
ID:(4661, 0)
Power depending on the temperature
Equation
When the particles of a medium oscillate, they act like small antennas emitting radiation. The power of this emitted radiation is related to the temperature of the medium and depends on the oscillation itself. This relationship between the emitted power and the absolute temperature is described by the Stefan-Boltzmann law, which states the following for a surface of area $S$:
where $\sigma$ is the Stefan-Boltzmann constant (with a value of $5.67 \times 10^{-8} W/m^2K^4$), $\epsilon$ is the emissivity, and $T$ is the absolute temperature of the medium.
Emissivity is a constant that indicates how perfectly a surface emits radiation and is closely related to its roughness. A smooth surface has an emissivity close to unity, which means it efficiently emits radiation. On the other hand, a surface with lower emissivity, which can have values between 0.2 and 0.4, has difficulty emitting radiation or may even reabsorb it, reducing the total flux of emitted radiation.
ID:(4664, 0)
Surface of a sphere
Equation
The surface area of a sphere with radius $r$ can be calculated using the following formula:
ID:(4665, 0)
Intensity depending on solar power
Equation
The intensity is defined as the power per unit area
| $ I =\displaystyle\frac{ P }{ S }$ |
If we consider an imaginary sphere with a radius equal to the distance between the sun and the earth, we can calculate its cross-sectional area
| $ S = 4 \pi R ^2$ |
This allows us to obtain the resulting intensity:
ID:(4662, 0)
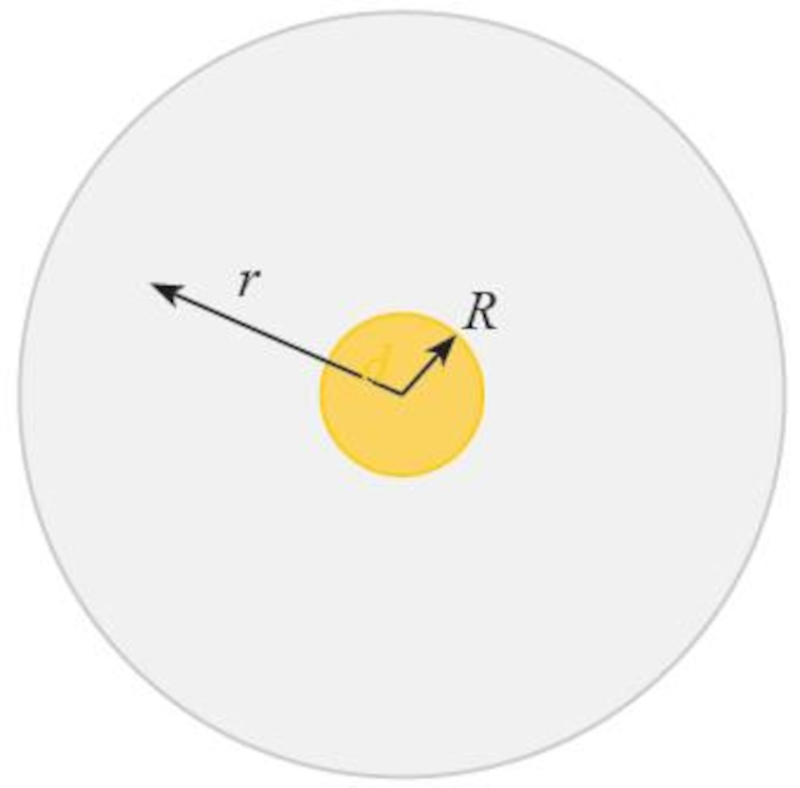
Radius of the orbit of the earth and the sun
Description
The radiation from the Sun flows through its surface, which has an area of $4\pi R^2$ with a radius of $R$, and is distributed at the height of the Earth's orbit, which has a surface area of $4\pi r^2$:
None
ID:(3082, 0)
Intensity depending on solar intensity
Equation
If we replace the solar power, calculated as the intensity at its surface
| $ P =4 \pi R ^2 I_R $ |
in the equation for the intensity of sunlight at the sun-earth distance
| $ I_p =\displaystyle\frac{ P }{4 \pi r ^2}$ |
we can obtain the relationship between intensities:
ID:(4663, 0)
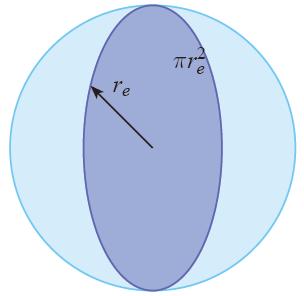
Area on earth that captures radiation
Description
The Earth presents a disk with an area of $\pi r_e^2$ exposed to solar radiation:
ID:(3084, 0)
Intensidad media recibida por la Tierra
Equation
Si
$4\pi R^2 I_s=\pi R^2 I_e$
Por la intensidad media sobre la tierra con es
| $ I_s =\displaystyle\frac{1}{4} I_p $ |
ID:(4667, 0)
Power captured by the ground
Equation
Since the Earth can only capture a fraction of the intensity from the Sun-Earth distance,
| $ I =\displaystyle\frac{ P }{ S }$ |
represented by the surface disk with a fraction of
| $ S = \pi r ^2$ |
,
the power captured by the Earth is calculated as
.
ID:(4666, 0)
