Utilisateur:
Rayonnement infrarouge
Storyboard 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Si la Terre est une temp rature $T_s$, elle met un rayonnement, principalement des longueurs d'onde $\lambda > 750$ nm, avec une puissance donn e par la loi de Stefan-Boltzmann :
o $\sigma$ est la constante de Stefan-Boltzmann, $\epsilon$ est l' missivit et $S$ est la surface d\' mission.
L\'intensit du rayonnement est d finie comme la puissance par unit de surface, donc on peut l\'exprimer comme suit :
o $S$ est la surface d\' mission.
Ainsi, l\'intensit mise depuis la surface de la Terre $I_e$ est donn e par:
o $T_e$ est la temp rature et $\epsilon$ est l\' missivit de la surface.
Exemples
Tout comme pour le rayonnement visible, l'atmosph re interagit avec le rayonnement infrarouge. De la m me mani re que l'interaction avec l'atmosph re est mod lis e pour le rayonnement visible en utilisant a couverture visible (VIS) ($\gamma_v$), on peut introduire ERROR:7452 qui affecte le rayonnement infrarouge.
Par cons quent, a intensité NIR émise par la Terre vers l'espace ($I_{es}$) est gal a intensité NIR émise par la terre ($I_e$) pond r par un facteur qui d pend de ERROR:7452, de sorte que :
De la radiation terrestre $I_e$, qui pour la plupart
La fraction de radiation qui interagit avec l'atmosph re est calcul e en utilisant la couverture $\gamma$ selon
Si la Terre est une temp rature $T_e$, elle met un rayonnement conform ment la loi de Stefan-Boltzmann, avec une intensit donn e par la formule suivante:
O $\sigma$ est la constante de Stefan-Boltzmann et $\epsilon$ est le coefficient d' missivit . La constante de Stefan-Boltzmann $\sigma$ a une valeur d'environ $5.67 \times 10^{-8} W/m^2K^4$, et le coefficient d\' missivit $\epsilon$ repr sente l\'efficacit avec laquelle la surface de la Terre met du rayonnement, variant de 0 1.
L'intensit $I$ mise par un corps une temp rature $T$ est r gie par la loi de Stefan-Boltzmann, exprim e comme suit :
o $\epsilon$ est l\' missivit et $\sigma$ est la constante de Stefan-Boltzmann. Ainsi, dans le cas du bord inf rieur du nuage, qui a une temp rature $T_b$, l\'intensit sera :
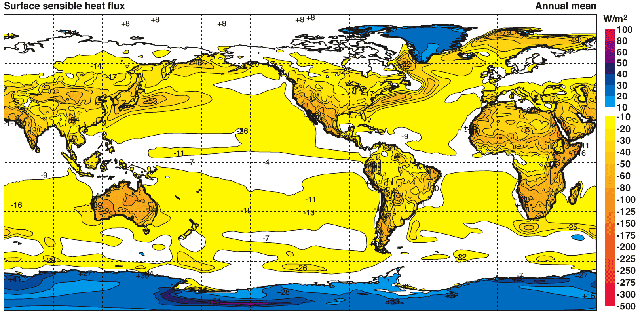
Si nous observons la distribution de la chaleur transport e par convection la surface de la plan te, nous pouvons remarquer qu'il existe des niveaux plus ou moins constants. D'une part, nous avons les zones oc aniques et continentales avec un flux d'environ $17 W/m^2$ (ascendant) et environ $-30 W/m^2$ (descendant) dans les zones couvertes de neige et de glace :
Ces donn es proviennent d'une r analyse de 40 ans r alis e par Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005 : ERA-40 Atlas. Reading, Royaume-Uni, Projet de r analyse de l'ECMWF (Kallberg et al., 2005).
En mod lisant a énergie transmise par conduction et évaporation ($I_d$), on peut tablir une relation pour le transport de chaleur qui inclut la diff rence entre ERROR:6516 et a température du fond de l'atmosphère ($T_b$), ainsi que ERROR:8094, qui est cl dans le processus. L' quation implique deux constantes, ERROR:8093 et ERROR:6521, de sorte que :
ERROR:8093 est de l'ordre de 10,0 W/m et ERROR:6521 est de l'ordre de 0,16 W/m K, avec ERROR:8094 typiquement autour de 8 m/s.
ERROR:8093 provient principalement de l' nergie transport e par le mouvement des masses d'air humide, qui lib rent de l' nergie lors de la condensation. ERROR:6521 est issu du transport d'air par convection et de l'expansion adiabatique correspondante, de sorte qu'il d pend principalement du gradient de temp rature.
A intensité rayonnée ($I_i$) est la fraction d finie par ERROR:8393 de ERROR:8390, calcul e de la mani re suivante :
A intensité rayonnée ($I_t$) est gal ERROR:8390 diminu de ERROR:8393, de sorte que :
La loi de Stefan-Boltzmann stipule que a intensité rayonnée ($I$) est une fonction de a température ($T$), utilisant les constantes a émissivité ($\epsilon$) et a stefan Boltzmann constant ($\sigma$), comme suit :
La loi de Stefan-Boltzmann stipule que a intensité rayonnée ($I$) est une fonction de a température ($T$), utilisant les constantes a émissivité ($\epsilon$) et a stefan Boltzmann constant ($\sigma$), comme suit :
La loi de Stefan-Boltzmann stipule que a intensité rayonnée ($I$) est une fonction de a température ($T$), utilisant les constantes a émissivité ($\epsilon$) et a stefan Boltzmann constant ($\sigma$), comme suit :
A énergie transmise par conduction et évaporation ($I_d$) d pend de la diff rence entre a température du fond de l'atmosphère ($T_b$) et ERROR:6516, ainsi que de ERROR:8094 et des constantes ERROR:8093 et ERROR:6521, de la mani re suivante :
ID:(536, 0)
