Tension superficielle
Concept 
Les molécules à l'intérieur d'un liquide subissent des attractions égales envers toutes leurs voisines. Cela a pour conséquence que les forces globalement exercées s'annulent mutuellement, faisant en sorte que la molécule se comporte comme une particule libre.
Cependant, la situation est différente pour les molécules à la surface. Étant donné qu'il y a plus de molécules à l'intérieur du liquide générant une force effective vers l'intérieur, cela empêche les molécules à la surface de quitter le liquide.
La force décrite dans la section précédente donne naissance à ce que l'on appelle la ERROR:tension superficielle. Cette tension superficielle crée une sorte de membrane à la surface, ce qui permet à certains insectes de se déplacer sur celle-ci sans couler. Par exemple, la patte de l'araignée sur l'image ne pénètre pas la surface, évitant ainsi de couler.La tension superficielle est également responsable de la forme des gouttes d'eau. L'attraction entre les molécules tend à faire en sorte que la goutte ait la plus petite surface possible, ce qui signifie qu'elle cherchera à adopter une forme sphérique. Cela fait qu'un jet d'eau a tendance à se briser en gouttes, et ces gouttes ont tendance à être sphériques ou à fluctuer autour de cette forme.
ID:(1551, 0)
Représentation graphique du travail obtenu
Image 
Étant donné que le travail est
| $ \delta W = p dV $ |
il peut être représenté sur un graphique pression-volume comme la zone sous la courbe de pression en fonction du volume :
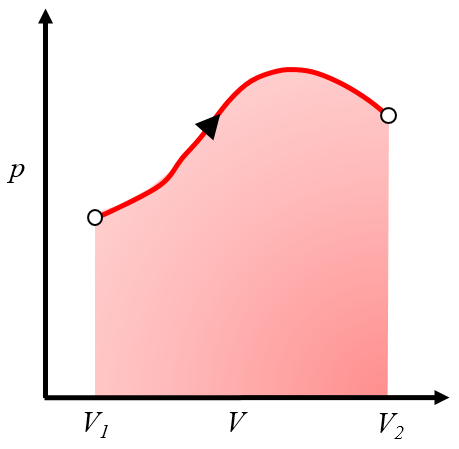
Cette zone représente le travail obtenu lorsque un gaz effectue un travail en s'expansant du volume $V_1$ au volume $V_2$.Généralement, ce processus est réalisé en chauffant le système, ce qui le fait s'étendre et effectuer le travail. Un exemple serait un piston avec du gaz chauffé dans une chaudière.
ID:(10266, 0)
Représentation graphique des travaux à investir
Image 
Pour répéter le processus, il est nécessaire de revenir du volume $V_2$ au volume $V_1$, ce qui signifie suivre une courbe dans le diagramme pression-volume dans le sens inverse :
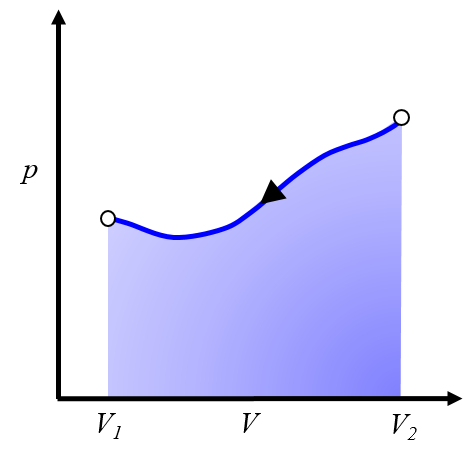
Cela représente un travail à investir, que nous devons fournir pour répéter le cycle.Généralement, ce processus est réalisé en refroidissant le système, ce qui le fait se contracter. L'énergie à investir correspond à la chaleur retirée du système.
ID:(10254, 0)
Représentation graphique du travail effectif obtenu
Image 
Le travail net obtenu est la différence entre le travail obtenu et le travail nécessaire pour compléter le cycle :
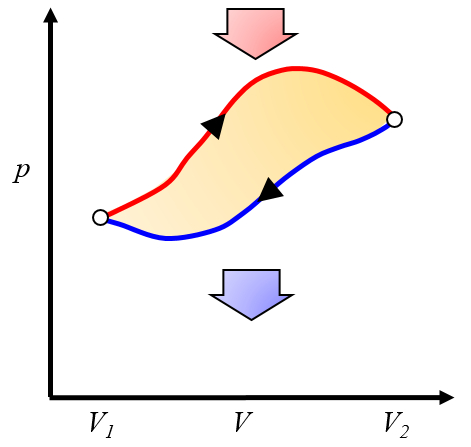
ID:(10268, 0)
Modèle simplifié
Image 
Une manière simple de modéliser une machine thermodynamique consiste à supposer qu'elle fonctionne de manière isotherme et adiabatique.
| $ W =\displaystyle\oint_C T dS $ |
Cela peut être représenté dans l'espace température versus entropie, où l'on observe deux segments isothermes et deux segments adiabatiques :

ID:(10257, 0)
Performances en fonction des températures
Concept 
A efficacité ($\eta$) est une fonction de le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donnée par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous pouvons exprimer le chaleur fournie ($Q_H$) en termes de a basse température ($T_C$), a faible entropie ($S_C$), et a haute entropie ($S_H$) comme suit :
| $ Q_C = T_C ( S_H - S_C ) $ |
Et en utilisant a température haute ($T_H$) comme suit :
| $ Q_H = T_H ( S_H - S_C ) $ |
Si nous substituons ces expressions, nous obtenons :
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
ID:(10260, 0)
Performance en fonction de la chaleur
Concept 
Étant donné que a efficacité ($\eta$) avec le travail efficace ($W$) et le chaleur fournie ($Q_H$) est
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
il peut être remplacé par le travail efficace ($W$) qui, avec le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donne
| $ W = Q_H - Q_C $ |
fournissant la relation suivante :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
ID:(10262, 0)
Travail effectué
Concept 
Puisque le différentiel de travail inexact ($\delta W$) est défini en fonction de a pression ($p$) et a variation de volume ($\Delta V$) comme suit :
| $ \delta W = p dV $ |
Nous pouvons calculer le travail efficace ($W$) en intégrant le long des courbes du diagramme du cycle :
$W = \displaystyle\oint pdV$
En utilisant le premier principe de la thermodynamique avec le différentiel d'énergie interne ($dU$) et le différence de chaleur inexacte ($\delta Q$) :
| $ dU = \delta Q - \delta W $ |
Et en tenant compte du parcours dans le diagramme de a température absolue ($T$) et a entropie ($S$), nous obtenons avec a variation d'entropie ($dS$) :
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
Étant donné que l'intégrale le long d'un chemin fermé d'une différentielle exacte est égale à zéro, nous avons :
| $ W = \displaystyle\oint T dS$ |
ID:(10264, 0)
Modèle plus complexe
Image 
Un modèle plus réaliste peut être développé en utilisant un gaz idéal, où :
Il s'étend d'un volume $V_1$ à $V_2$ de manière isotherme à une température $T_H$.
Ensuite, il continue à s'étendre d'un volume $V_2$ à un volume $V_3$ de manière adiabatique, en refroidissant de la température $T_H$ à $T_C$.
Ensuite, il se contracte de manière isotherme d'un volume $V_3$ à un volume $V_4$ tout en maintenant une température de $T_C$.
Enfin, il continue à se contracter d'un volume $V_4$ à un volume $V_1$ de manière adiabatique, en se réchauffant de la température $T_C$ à $T_H$.
Cela est résumé dans le graphique suivant :

Le processus effectue un travail au point 1 via la route 2 à 3, tandis que le travail doit être effectué à partir du point 3 via la route 4 à 1. Cela est réalisé en fournissant de la chaleur dans la première étape et en extrayant de la chaleur dans la deuxième.
ID:(10267, 0)
Formation de gouttelettes
Modèle 
Variables
Calculs
Calculs
Équations
Exemples
(ID 15292)
(ID 15350)
Les mol cules l'int rieur d'un liquide subissent des attractions gales envers toutes leurs voisines. Cela a pour cons quence que les forces globalement exerc es s'annulent mutuellement, faisant en sorte que la mol cule se comporte comme une particule libre.
Cependant, la situation est diff rente pour les mol cules la surface. tant donn qu'il y a plus de mol cules l'int rieur du liquide g n rant une force effective vers l'int rieur, cela emp che les mol cules la surface de quitter le liquide.
La force d crite dans la section pr c dente donne naissance ce que l'on appelle la ERROR:tension superficielle. Cette tension superficielle cr e une sorte de membrane la surface, ce qui permet certains insectes de se d placer sur celle-ci sans couler. Par exemple, la patte de l'araign e sur l'image ne p n tre pas la surface, vitant ainsi de couler.La tension superficielle est galement responsable de la forme des gouttes d'eau. L'attraction entre les mol cules tend faire en sorte que la goutte ait la plus petite surface possible, ce qui signifie qu'elle cherchera adopter une forme sph rique. Cela fait qu'un jet d'eau a tendance se briser en gouttes, et ces gouttes ont tendance tre sph riques ou fluctuer autour de cette forme.
(ID 1551)
tant donn que le travail est
| $ \delta W = p dV $ |
il peut tre repr sent sur un graphique pression-volume comme la zone sous la courbe de pression en fonction du volume :

Cette zone repr sente le travail obtenu lorsque un gaz effectue un travail en s'expansant du volume $V_1$ au volume $V_2$.G n ralement, ce processus est r alis en chauffant le syst me, ce qui le fait s' tendre et effectuer le travail. Un exemple serait un piston avec du gaz chauff dans une chaudi re.
(ID 10266)
Pour r p ter le processus, il est n cessaire de revenir du volume $V_2$ au volume $V_1$, ce qui signifie suivre une courbe dans le diagramme pression-volume dans le sens inverse :

Cela repr sente un travail investir, que nous devons fournir pour r p ter le cycle.G n ralement, ce processus est r alis en refroidissant le syst me, ce qui le fait se contracter. L' nergie investir correspond la chaleur retir e du syst me.
(ID 10254)
Le travail net obtenu est la diff rence entre le travail obtenu et le travail n cessaire pour compl ter le cycle :

(ID 10268)
Une mani re simple de mod liser une machine thermodynamique consiste supposer qu'elle fonctionne de mani re isotherme et adiabatique.
| $ W =\displaystyle\oint_C T dS $ |
Cela peut tre repr sent dans l'espace temp rature versus entropie, o l'on observe deux segments isothermes et deux segments adiabatiques :

(ID 10257)
A efficacité ($\eta$) est une fonction de le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donn e par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous pouvons exprimer le chaleur fournie ($Q_H$) en termes de a basse température ($T_C$), a faible entropie ($S_C$), et a haute entropie ($S_H$) comme suit :
| $ Q_C = T_C ( S_H - S_C ) $ |
Et en utilisant a température haute ($T_H$) comme suit :
| $ Q_H = T_H ( S_H - S_C ) $ |
Si nous substituons ces expressions, nous obtenons :
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
(ID 10260)
tant donn que a efficacité ($\eta$) avec le travail efficace ($W$) et le chaleur fournie ($Q_H$) est
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
il peut tre remplac par le travail efficace ($W$) qui, avec le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donne
| $ W = Q_H - Q_C $ |
fournissant la relation suivante :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
(ID 10262)
Puisque le différentiel de travail inexact ($\delta W$) est d fini en fonction de a pression ($p$) et a variation de volume ($\Delta V$) comme suit :
| $ \delta W = p dV $ |
Nous pouvons calculer le travail efficace ($W$) en int grant le long des courbes du diagramme du cycle :
$W = \displaystyle\oint pdV$
En utilisant le premier principe de la thermodynamique avec le différentiel d'énergie interne ($dU$) et le différence de chaleur inexacte ($\delta Q$) :
| $ dU = \delta Q - \delta W $ |
Et en tenant compte du parcours dans le diagramme de a température absolue ($T$) et a entropie ($S$), nous obtenons avec a variation d'entropie ($dS$) :
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
tant donn que l'int grale le long d'un chemin ferm d'une diff rentielle exacte est gale z ro, nous avons :
| $ W = \displaystyle\oint T dS$ |
(ID 10264)
Un mod le plus r aliste peut tre d velopp en utilisant un gaz id al, o :
Il s' tend d'un volume $V_1$ $V_2$ de mani re isotherme une temp rature $T_H$.
Ensuite, il continue s' tendre d'un volume $V_2$ un volume $V_3$ de mani re adiabatique, en refroidissant de la temp rature $T_H$ $T_C$.
Ensuite, il se contracte de mani re isotherme d'un volume $V_3$ un volume $V_4$ tout en maintenant une temp rature de $T_C$.
Enfin, il continue se contracter d'un volume $V_4$ un volume $V_1$ de mani re adiabatique, en se r chauffant de la temp rature $T_C$ $T_H$.
Cela est r sum dans le graphique suivant :

Le processus effectue un travail au point 1 via la route 2 3, tandis que le travail doit tre effectu partir du point 3 via la route 4 1. Cela est r alis en fournissant de la chaleur dans la premi re tape et en extrayant de la chaleur dans la deuxi me.
(ID 10267)
ID:(1333, 0)
