Druyd:Knowledge

Ejemplo del Camino Aleatorio (Random Walk)

Storyboard

El camino aleatorio es un típico ejemplo como partiendo de probabilidades microscópicas (el paso a la derecha o izquierda) se logra desarrollar una distribución de probabilidades que da cuenta de los lugares mas probables en que se puede encontrar al caminante.

>Modelo

ID:(308, 0)

Problema del random walk (camino aleatorio)

Definición

ID:(11396, 0)

Distribución binomial

Imagen

ID:(11397, 0)

Ejemplo del Camino Aleatorio (Random Walk)

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$C_{n_1n_2}$

C_n1n2

Combinaciones posibles de (n_1,n_2) caminos

$a$

Largo del paso

$n_1$

n_1

Número de pasos hacia la derecha

$n_2$

n_2

Número de pasos hacia la izquierda

$N$

Número total de pasos

$n$

Número totales de pasos a la derecha

$s$

Posición camino aleatorio

$p_{n_1n_2}$

p_n1n2

Probabilidad de avanzar una combinación (n_1,n_2)

$P_N(m)$

P_Nm

Probabilidad de hacer un numero de pasos hacia la derecha

$p$

Probabilidad de pasos hacia la derecha

$q$

Probabilidad de pasos hacia la izquierda

$W_N(n_1,n_2)$

W_n1n2

Probabilidad de realizar (n_1,n_2) pasos cualquier secuencia

$p_{n_1,n_2}$

p_n1n2

Probabilidad de realizar (n_1,n_2) pasos en secuencia

$\Delta t$

Tiempo del paso

$t$

Tiempo final

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ t = N \Delta t $

t = N * Dt

(ID 501)

$x=(n_1-n_2)a$

x=(n_2-n_1)a

(ID 503)

$p_{n_1n_2}=p^{n_1}q^{n_2}$

p_{n_1n_2}=p^{n_1}q^{n_2}

(ID 504)

$C_{n_1n_2}=\displaystyle\frac{N!}{n_1!n_2!}$

C_n1n2=N!/(n_1!n_2!)

(ID 505)

$N=n_1+n_2$

N = n_1 + n_2

(ID 3358)

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))

(ID 8961)

$p+q=1$

p+q=1

(ID 8965)

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$

W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}

(ID 8970)

$W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}$

W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}

(ID 8980)

Ejemplos

Problema del random walk (camino aleatorio)

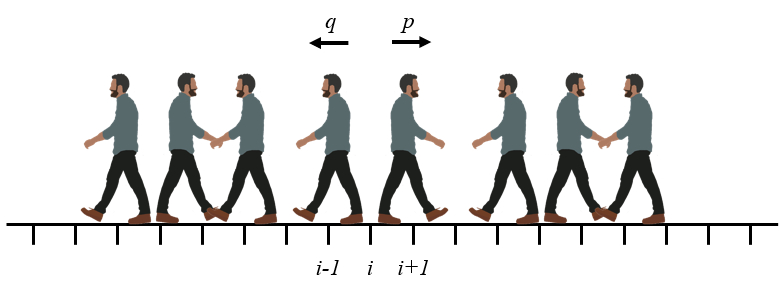
El problema del camino aleatorio es un ejemplo de como uno puede desde la descripci n microsc pica pronosticar la probable evoluci n temporal. En este caso se asume que un actor (part cula, persona, etc.) escoge al azar si va a dar un paso a la derecha o a la izquierda. Se asume que los pasos tienen un largo a y que la probabilidad de ir a la derecha es p y a la izquierda q:

(ID 11396)

Distribuci n binomial

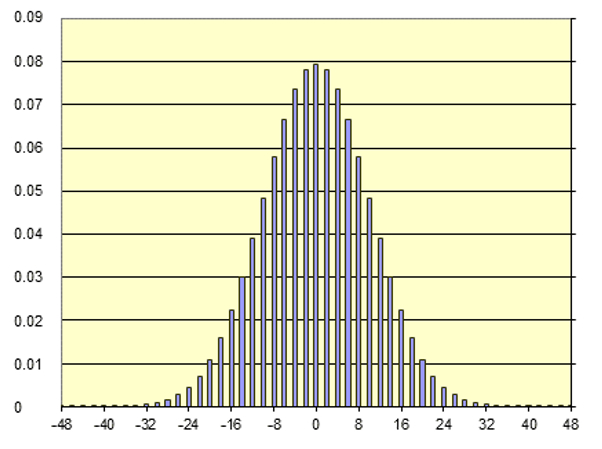
El resultado del calculo corresponde a lo que se denomina una distribuci n binomial. Cada linea indica la fracci n de veces que tras un numero N de pasos el actor termine en dicha posici n. Esto corresponde a la probabilidad de encontrarlo tras N pasos en esa ubicaci n:

(ID 11397)

ID:(308, 0)