Druyd:Knowledge

Modelo Clásico del Solido

Storyboard

Los modelos mas simples son aquellos que asumen que el solido se puede modelar como una colección de resortes que ligan los vecinos más próximos.

>Modelo

ID:(838, 0)

Modelo de Drude de un solido

Imagen

En 1904 Paul Drude propuso modelar un solido (cristal) como una grilla con átomos que interactuan de modo de formar pequeños osciladores.

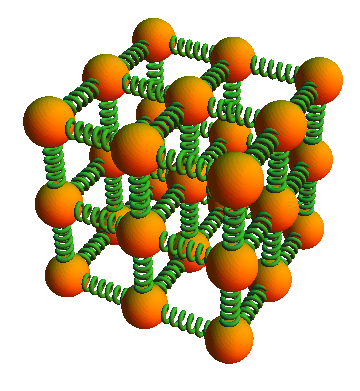
Átomos ligados con conectores tipo resortes

ID:(9507, 0)

Modelo Clásico del Solido

Modelo

Los modelos mas simples son aquellos que asumen que el solido se puede modelar como una colección de resortes que ligan los vecinos más próximos.

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$\beta$

beta

Beta

kg m/s

$k_B$

k_B

Constante de Boltzmann

J/K

$h$

Constante de Planck

kg m/s

$k_s$

k_s

Constante del resorte

N/m

$V_0$

V_0

Energía potencial de deformación macroscopica

$V$

Energía potencial entre partículas

$Z$

Función partición del solido clásico

$\ln Z$

ln Z

Logaritmo de la función partición del solido clásico

$m$

Masa de la partícula

$p_i$

p_i

Momento de la partícula i

kg m/s

$N$

Numero de partículas

$q$

Posición de la partícula

$q_i$

q_i

Posición de la partícula i

$q_j$

q_j

Posición de la partícula j

$q_0$

q_0

Posición del origen de la partícula

$T$

Temperatura

$\Theta_s$

Theta_s

Temperatura de referencia clásica

$V$

Volumen del cuerpo

m^3

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ Z_s =\displaystyle\frac{1}{ h ^{3 N } N !}\int\prod_i d^3 p_i \prod_i d^3 q_i e^{- \beta \sum_i( p_i ^2/2 m +V(q_i)) }$

Z_s =(1/( h ^(3* N )* N !))*@INT( @PROD(d^3 p_i , i )*@PROD( d^3 q_i , i )*exp(- beta *@SUM( p_i ^2/2m+ V(q_i) )

(ID 7984)

$ Z =\displaystyle\frac{1}{ h ^{3 N } N !}\left(\displaystyle\frac{2 \pi m }{ \beta }\right)^{3 N /2} V ^ N e^{- N \beta V_0 }$

Z =(1/ h ^(3* N )* N !)*(2* pi * m / beta )^3*( N /2)* V ^ N exp( - beta * V_0 * N )

(ID 8023)

$ Z =\displaystyle\frac{1}{ h ^{3 N }}\left(\displaystyle\frac{2 \pi }{\beta}\right)^{3 N }\left(\displaystyle\frac{ m a ^2}{ V_a }\right)^{3 N /2}e^{-3 N \beta V_0 }$

Z =(2* pi / beta )^(3* N )*( m * a ^2/ V_a )^(3* N /2)*e^(-3 * N * beta * V_0 )/( h ^(3* N ))

(ID 8024)

$ V = V_0 $

V = V_0

(ID 9502)

$ V(q_i,q_j) = V(q_i) \delta_{ij} $

V(q_i,q_j) = V(q_i) * delta_ij

(ID 9503)

$ V(q) = V_0 + \displaystyle\frac{1}{2} V_a \left(\displaystyle\frac{ q }{ a }\right)^2$

V = V_0 + V_a * ( q / a )^2/2

(ID 9504)

$ \Theta_s \equiv \displaystyle\frac{ \hbar }{ k_B }\sqrt{\displaystyle\frac{ V_a }{ m a ^2}}$

Theta_s =( hbar / k_B )*sqrt( V_a /( m * a ^2))

(ID 9556)

$ Z_s = \left(\displaystyle\frac{ T }{ \Theta_s }\right)^{3 N } e^{-3 N V_0 / k_B T }$

Z_s = ( T / Theta_s )^(3 * N )*exp(-3* N * V_0 /( k_B * T ))

(ID 9557)

$ \ln Z_s =- 3 N \ln\left(\displaystyle\frac{ \Theta_s }{ T }\right)-\displaystyle\frac{3 N V_0 }{ k_B T } $

ln( Z_s )=- 3* N *ln( Theta_s / T )- 3* N * V_0 /( k_B * T )

(ID 9561)

$ Z_s = \displaystyle\frac{1}{( \beta k_B \Theta_s )^{3 N }} e^{-3 N \beta V_0 }$

Z_s =exp(-3 * N * V_0 /( k_B * T ))/( beta * k_B * Theta_s )^(3* N )

(ID 13652)

$ \ln Z_s =- 3 N \ln( \beta k_B \Theta_s )- 3 N \beta V_0 $

ln( Z_s )=- 3* N *ln( beta * k_B * Theta_s )- 3* N * beta * V_0

(ID 13653)

$ \omega_s \equiv \sqrt{\displaystyle\frac{ V_a }{ m a ^2}}$

omega_s =sqrt( V_a /( m * a ^2))

(ID 13654)

Ejemplos

Modelo de Drude de un solido

En 1904 Paul Drude propuso modelar un solido (cristal) como una grilla con tomos que interactuan de modo de formar peque os osciladores.

tomos ligados con conectores tipo resortes

(ID 9507)

ID:(838, 0)