Benützer:
Gleichgewichtszustand und Temperatur
Storyboard 
Um Systeme mit Hilfe der statistischen Mechanik zu modellieren, müssen wir untersuchen, wie die Parameter, die das makroskopische System beschreiben, die statistischen Ensembles beeinflussen können. Im Falle von Teilchen wird die Temperatur als Parameter festgelegt, der zeigt, ob die Systeme im Gleichgewicht sind und ihre Energien auf einem konstanten Niveau halten
ID:(436, 0)
Ein System in Kontakt mit einem Reservoir
Bild
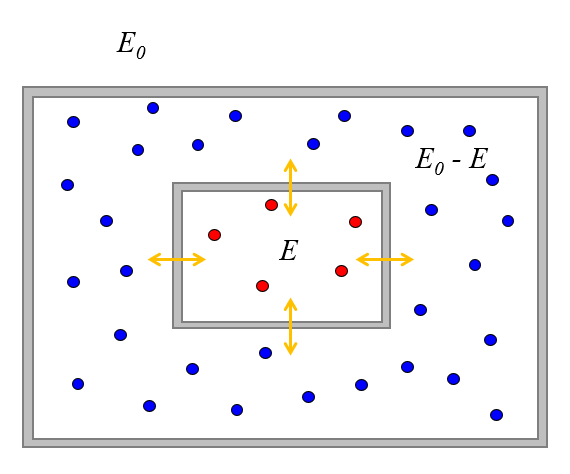
Wir können untersuchen, was passiert, wenn wir zwei Systeme von Teilchen in Kontakt bringen, so dass sie Energie, aber keine Teilchen austauschen können.
Angenommen, das System ist von seiner Umgebung isoliert, was bedeutet, dass es eine Gesamtenergie von $E_0$ hat.
Angenommen, zunächst hat das erste System eine Energie von $E$, die mit $\Omega(E)$ Zuständen verbunden ist.
Da die Gesamtenergie $E_0$ beträgt, kann das zweite System nur die Energie $E_0-E$ und eine Anzahl von verbundenen Zuständen $\Omega(E_0-E)$ haben.
Sobald wir sie in Kontakt bringen, können sie Energie austauschen, bis sie ein Gleichgewicht erreichen. In dieser Hinsicht wird der Wert von $E$ variieren, und die Wahrscheinlichkeit, die Systeme so zu finden, dass das erste einen Wert von $E$ hat, wird ebenfalls variieren.
ID:(11541, 0)
Vergleich der Anzahl der Zustandskurven
Bild
Wenn wir betrachten, wie sich die Anzahl der Zustände mit der Energie $E$ ändert, bemerken wir, dass sich das Verhalten des Systems und des Reservoirs entgegengesetzt verhält:
Dies geschieht, weil mit steigender Energie die Energie des Reservoirs abnimmt, was wiederum die Anzahl der erreichbaren Zustände reduziert.
ID:(11542, 0)
Bilden eines Maximums
Bild
Wenn wir die Anzahl der Fälle multiplizieren, erhalten wir eine Funktion mit einem sehr ausgeprägten Maximum.
Das System wird mit größerer Wahrscheinlichkeit bei der Energie gefunden, an der das Maximum der Wahrscheinlichkeitskurve auftritt.
ID:(11543, 0)
Gleichgewichtszustand und Temperatur
Modell
Um Systeme mit Hilfe der statistischen Mechanik zu modellieren, müssen wir untersuchen, wie die Parameter, die das makroskopische System beschreiben, die statistischen Ensembles beeinflussen können. Im Falle von Teilchen wird die Temperatur als Parameter festgelegt, der zeigt, ob die Systeme im Gleichgewicht sind und ihre Energien auf einem konstanten Niveau halten
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
(ID 3438)
Beispiele
Wir k nnen untersuchen, was passiert, wenn wir zwei Systeme von Teilchen in Kontakt bringen, so dass sie Energie, aber keine Teilchen austauschen k nnen.
Angenommen, das System ist von seiner Umgebung isoliert, was bedeutet, dass es eine Gesamtenergie von $E_0$ hat.
Angenommen, zun chst hat das erste System eine Energie von $E$, die mit $\Omega(E)$ Zust nden verbunden ist.
Da die Gesamtenergie $E_0$ betr gt, kann das zweite System nur die Energie $E_0-E$ und eine Anzahl von verbundenen Zust nden $\Omega(E_0-E)$ haben.
Sobald wir sie in Kontakt bringen, k nnen sie Energie austauschen, bis sie ein Gleichgewicht erreichen. In dieser Hinsicht wird der Wert von $E$ variieren, und die Wahrscheinlichkeit, die Systeme so zu finden, dass das erste einen Wert von $E$ hat, wird ebenfalls variieren.
(ID 11541)
Wenn wir betrachten, wie sich die Anzahl der Zust nde mit der Energie $E$ ndert, bemerken wir, dass sich das Verhalten des Systems und des Reservoirs entgegengesetzt verh lt:
Dies geschieht, weil mit steigender Energie die Energie des Reservoirs abnimmt, was wiederum die Anzahl der erreichbaren Zust nde reduziert.
(ID 11542)
Wenn wir die Anzahl der F lle multiplizieren, erhalten wir eine Funktion mit einem sehr ausgepr gten Maximum.
Das System wird mit gr erer Wahrscheinlichkeit bei der Energie gefunden, an der das Maximum der Wahrscheinlichkeitskurve auftritt.
(ID 11543)
ID:(436, 0)