Modelo de Drude de un solido
Bild 
En 1904 Paul Drude propuso modelar un solido (cristal) como una grilla con átomos que interactuan de modo de formar pequeños osciladores.
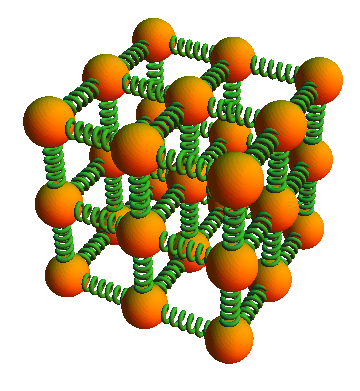
Átomos ligados con conectores tipo resortes
ID:(9507, 0)
Modelo Clásico del Solido
Modell 
Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$\beta$
beta
Beta
kg m/s
$k_B$
k_B
Constante de Boltzmann
J/K
$h$
h
Constante de Planck
kg m/s
$k_s$
k_s
Constante del resorte
N/m
$V_0$
V_0
Energía potencial de deformación macroscopica
J
$V$
V
Energía potencial entre partículas
J
$Z$
Z
Función partición del solido clásico
-
$\ln Z$
ln Z
Logaritmo de la función partición del solido clásico
-
$m$
m
Masa de la partícula
kg
$p_i$
p_i
Momento de la partícula i
kg m/s
$N$
N
Numero de partículas
-
$q$
q
Posición de la partícula
J
$q_i$
q_i
Posición de la partícula i
J
$q_j$
q_j
Posición de la partícula j
J
$q_0$
q_0
Posición del origen de la partícula
J
$T$
T
Temperatura
K
$\Theta_s$
Theta_s
Temperatura de referencia clásica
K
$V$
V
Volumen del cuerpo
m^3
Berechnungen
Zuerst die Gleichung auswählen:  zu
zu  ,
dann die Variable auswählen:
,
dann die Variable auswählen:  zu
zu 
Symbol
Gleichung
Gelöst
Übersetzt
Berechnungen
Symbol
Gleichung
Gelöst
Übersetzt
Gleichungen
(ID 9502)
Beispiele
En 1904 Paul Drude propuso modelar un solido (cristal) como una grilla con tomos que interactuan de modo de formar peque os osciladores.

tomos ligados con conectores tipo resortes
(ID 9507)
ID:(838, 0)
