Usuario:
La ley de reflexión
Imagen 
Aplicando el principio de Huygens se muestra que un haz que incide sobre una superficie se refleja bajo un angulo igual al de incidencia:
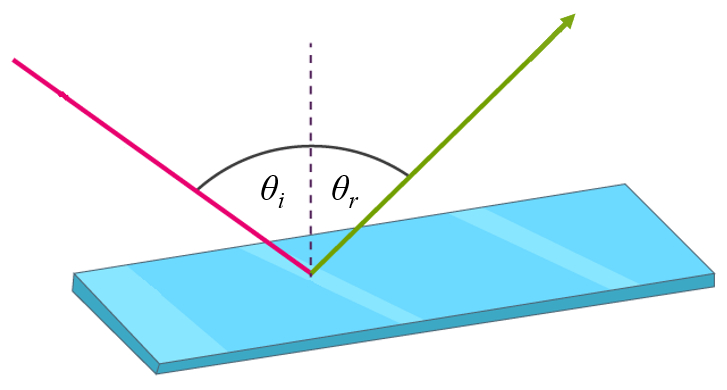
ID:(12758, 0)
Principio de Huygens: Reflexión, fuentes en superficie
Imagen
Si una onda plana arriba a una superficie, el principio de Huygens establece que se deben considerar fuentes que irradian estrictamente sobre la superficie:
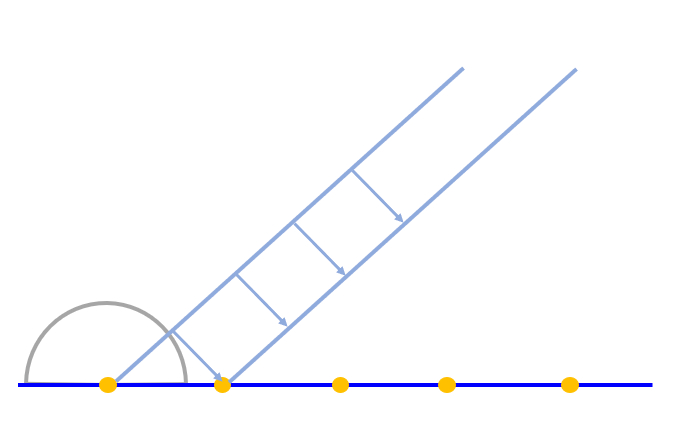
ID:(12660, 0)
Principio de Huygens: Reflexión, segunda fuente
Imagen
Tras la primera se cera una segunda fuente mientras la primera irradia estrictamente:
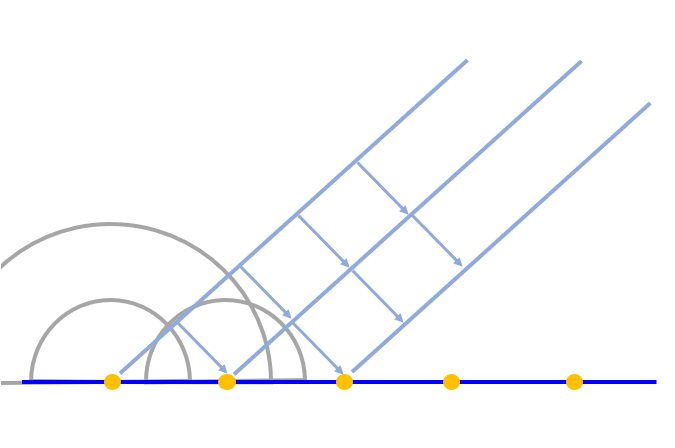
ID:(12661, 0)
Principio de Huygens: Reflexión, tercera fuente
Imagen
Tras la primera se cera una tercera fuente mientras las primeras dos irradia estrictamente:
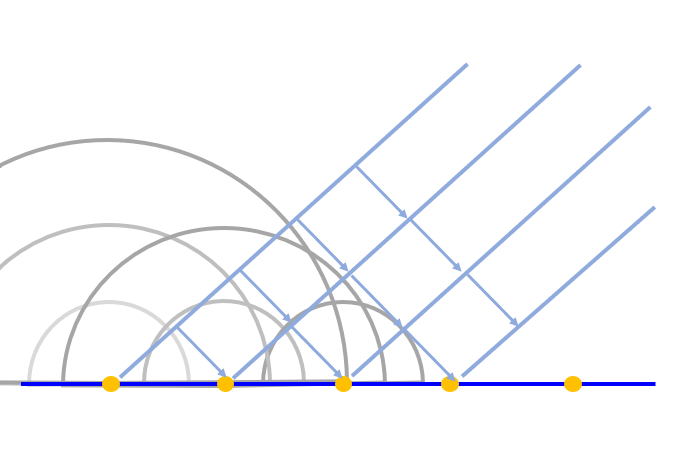
ID:(12662, 0)
Principio de Huygens: Ondas de incidencia y reflexión
Imagen
Si se construye el frente de onda que se genera con las fuentes a lo largo de la pared muestra que se puede establecer una relación del angulo de incidencia (entre el haz de incidencia y la normal) y el de reflexión (entre el haz de reflexión y la normal):
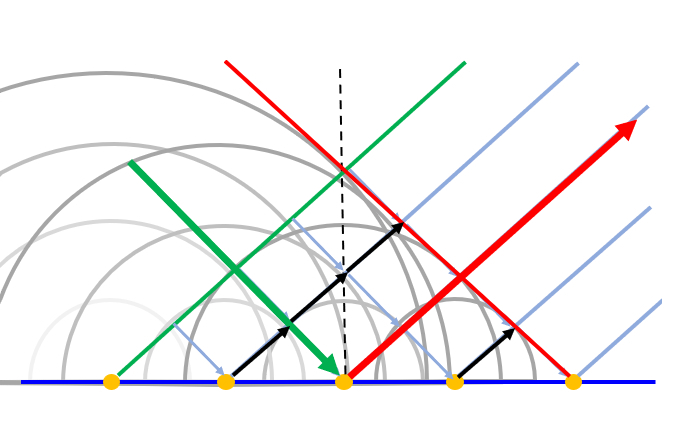
ID:(12663, 0)
Principio de Huygens: Angulo de incidencia y reflexión
Imagen
Si se observa el triangulo en el centro se ve que ambos catetos son iguales por efecto de ser la velocidad de la luz igual para ambos haces. Por ello el triangulo es simétrico y los ángulos
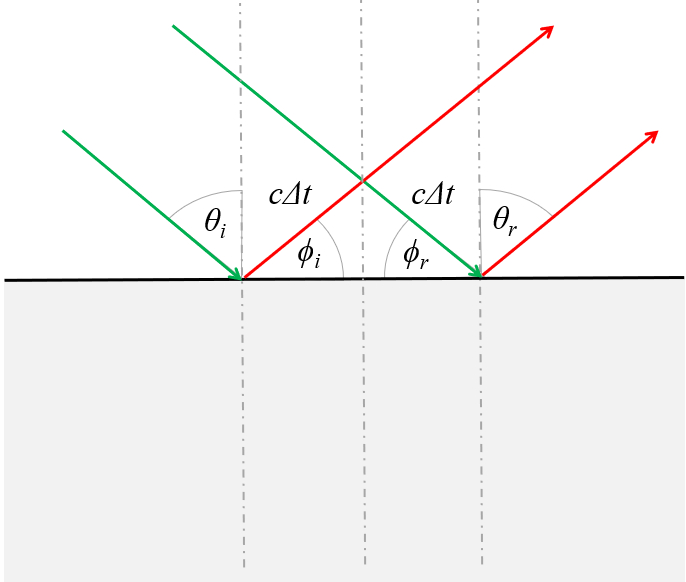
\\n\\nComo los ángulos respecto de la normal son\\n\\n
$\theta_i = \displaystyle\frac{1}{2}\pi - \phi_i$
\\n\\n
$\theta_r = \displaystyle\frac{1}{2}\pi - \phi_r$
por lo que el angulo de incidencia es igual al de reflexión.
ID:(12664, 0)
Relación entre ángulos de incidencia y reflexión
Imagen
Del análisis mediante el principio de Huygens se concluye que los ángulos de incidencia y reflexión son iguales:
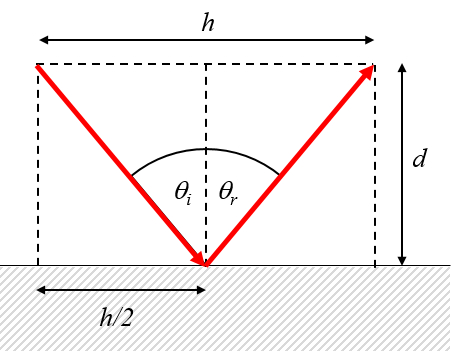
ID:(12665, 0)
Dirección de la Luz reflejada
Ecuación
Para la luz reflejada el angulo del haz respecto de la normal
 $ \theta_i = \theta_r $ |
ID:(3262, 0)
Angulo complementario del angulo de reflexión
Ecuación
Para el calculo de los ángulos en el caso de que los haces se reflejan en un espejo es útil poder calcular el angulo complementario al de reflexión. Por ello se tiene que
| $ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $ |
Como la suma de los ángulos internos en un triangulo es
| $ \pi = \alpha + \beta + \gamma $ |
se tiene que en un rectángulo, en el que uno de los ángulos es
| $ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $ |
ID:(10925, 0)
Ángulo complementario del ángulo de incidencia
Ecuación
Para el calculo de los ángulos en el caso de que los haces se reflejan en un espejo es útil poder calcular el angulo complementario al de incidencia. Por ello se tiene que
| $ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $ |
Como la suma de los ángulos internos en un triangulo es
| $ \pi = \alpha + \beta + \gamma $ |
se tiene que en un rectángulo, en el que uno de los ángulos es
| $ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $ |
ID:(10928, 0)
Suma de ángulo de un triángulo
Ecuación
| $ \pi = \alpha + \beta + \gamma $ |
ID:(10926, 0)
Relación entre ángulos de incidencia y reflexión
Imagen
En caso de dos espejos con una esquina
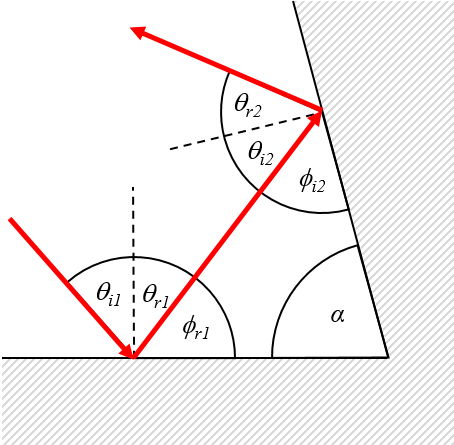
se pueden calcular los ángulos con la relación de reflexión
| $ \theta_i = \theta_r $ |
el calculo del complemento del angulo incidente
| $ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $ |
el calculo del complemento del angulo de reflección
| $ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $ |
y la relación entre los ángulos de un triangulo
| $ \pi = \alpha + \beta + \gamma $ |
ID:(12666, 0)
Angulo de incidencia
Ecuación
El angulo de incidencia
| $ \tan \theta_i =\displaystyle\frac{ h }{2 d }$ |
ID:(9779, 0)
0
Video
Video: Reflexión