User:
Radiant Flux
Storyboard 
The light is irradiated, that is to say it flows so that the fundamental magnitudes refer to the amount of photons that are emitted, cross a section or are absorbed.
Since the amount of photons in a color is proportional to the energy, the flow is proportional to the energy per time, that is, the power.
ID:(297, 0)
Decrease in intensity with distance
Definition
If we think of light as a flow of photons, they will move away from their source and spread over an increasingly larger surface:
In this way, the intensity decreases as we move away from the source, diminishing inversely with the square of the distance.
ID:(1664, 0)
Brightness of Light by Hole
Image
When light passes through the aperture, the intensity depends on the angle of the beam relative to the original direction of the beam, denoted as $\theta$.
The intensity $I$ is given by
 $I(r,\theta)=\displaystyle\frac{r_0^2}{r^2}I_0\cos\theta$
|
ID:(3352, 0)
Light travelling through an Slite
Note
When light passes through an aperture, it begins to disperse. Its intensity decreases both with the distance from the aperture and with the angle relative to the original direction of propagation:
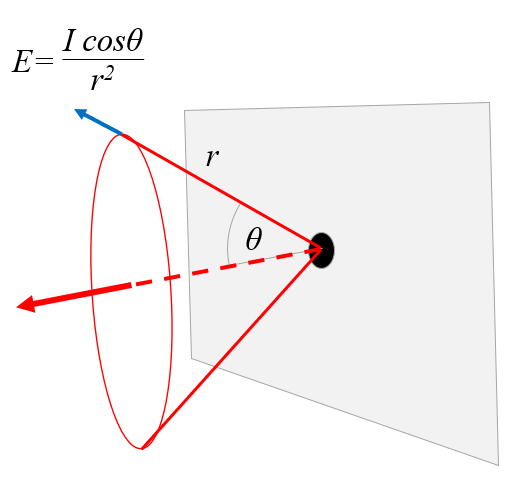
ID:(1861, 0)
Radiant Flux
Description
The light is irradiated, that is to say it flows so that the fundamental magnitudes refer to the amount of photons that are emitted, cross a section or are absorbed. Since the amount of photons in a color is proportional to the energy, the flow is proportional to the energy per time, that is, the power.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
If we think of light as a flow of photons, they will move away from their source and spread over an increasingly larger surface:
In this way, the intensity decreases as we move away from the source, diminishing inversely with the square of the distance.
(ID 1664)
When light passes through the aperture, the intensity depends on the angle of the beam relative to the original direction of the beam, denoted as $\theta$.
The intensity $I$ is given by
| $I(r,\theta)=\displaystyle\frac{r_0^2}{r^2}I_0\cos\theta$ |
(ID 3352)
When light passes through an aperture, it begins to disperse. Its intensity decreases both with the distance from the aperture and with the angle relative to the original direction of propagation:
(ID 1861)
Since photons are distributed over an area of size $4\pi r^2$, the number per unit area of these photons decreases. As the number of photons per unit area is the density, it reduces as follows:
| $ I_r =\displaystyle\frac{ r_0 ^2}{ r ^2} I_0 $ |
Intensity is measured in candelas (cd), which is the amount of light emitted by an object at a temperature of $2042.5 K$ over an area of size $1/600000 m^2$.
(ID 3191)
ID:(297, 0)