Arc-en-ciel
Définition 
Si vous observez un arc-en-ciel, vous verrez en réalité qu'il y a plusieurs arcs-en-ciel et que la séquence de couleurs se déplace : du bleu au rouge, puis du rouge au bleu, et ainsi de suite.

ID:(1844, 0)
Le spectre
Image 
Como l'angle de réfraction dépend de la fréquence ou de la longueur d'onde de la lumière dans le verre, on peut utiliser un prisme pour décomposer la lumière en ses différentes couleurs.

On obtient ce que l'on appelle le spectre de la lumière.
ID:(6972, 0)
La lumière et ses couleurs
Noter 
Un arc-en-ciel nous montre que la lumière qui l'illumine se décompose en plusieurs couleurs. En fait, si on l'observe attentivement, on peut voir qu'il existe plusieurs arcs-en-ciel.
Cela s'explique par le fait que chaque goutte d'eau agit comme un petit prisme circulaire, ce qui permet de multiples réfractions et la création de plusieurs arcs-en-ciel.
ID:(1625, 0)
Spectre newtonien
Citation 
Newton a utilisé un prisme pour décomposer la lumière en ses composants, croyant qu'il pouvait identifier un nombre fini de couleurs :

ID:(1682, 0)
Sir Isaac Newton
Exercer 
Le premier à comprendre la structure de la lumière en tant qu'entité physique fut Sir Isaac Newton.

Sir Isaac Newton
(1643-1727)
Grâce à une expérience très simple, il démontra que la lumière blanche était composée de couleurs. Cependant, il croyait que le nombre de couleurs était discret, comme le montre son graphique représentant ses observations.
ID:(6971, 0)
La réalité des choses
Équation 
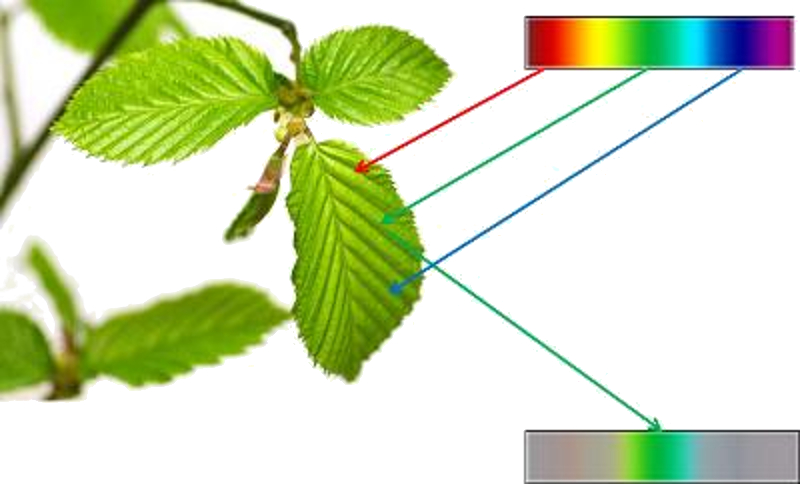
Les couleurs que nous voyons ne correspondent pas toujours nécessairement à la réalité. Nos yeux capturent la lumière et génèrent des impulsions électriques en fonction de la quantité de lumière bleue, rouge et verte que nous percevons. Cependant, l'intensité ne correspond pas toujours aux proportions réelles, ce qui entraîne une perception différente de la réalité :

ID:(12676, 0)
Lumière et couleurs
Description 
Variables
Calculs
Calculs
Équations
(ID 3341)
tant donn que le fréquence des photons ($\nu$) est l'inverse de le période ($T$) :
$\nu=\displaystyle\frac{1}{T}$
cela signifie que a surface de la fontaine ($c$) est gal la distance parcourue en une oscillation, c'est- -dire ERROR:8439, divis e par le temps coul , qui correspond la p riode :
$c=\displaystyle\frac{\lambda}{T}$
En d'autres termes, la relation suivante s'applique :
| $ c = \nu \lambda $ |
(ID 3953)
L' nergie d'une onde ou d'une particule (photon) de lumi re est donn e par
| $ \epsilon = h \nu $ |
Lorsque cette nergie se propage d'un milieu, par exemple, un vide avec une vitesse de la lumi re $c$, vers un autre milieu avec une vitesse de la lumi re $c_m$, on en d duit que la fr quence de la lumi re reste inchang e. Cependant, cela implique que, puisque la vitesse de la lumi re est gale au produit de la fr quence et de la longueur d'onde, comme indiqu dans l' quation
| $ c = \nu \lambda $ |
la longueur d'onde doit changer lorsqu'elle passe d'un milieu un autre.
Par cons quent, si nous avons une longueur d'onde de la lumi re dans un milieu $\lambda_m$ et dans le vide $\lambda$, l'indice de r fraction peut tre d fini comme
| $ n =\displaystyle\frac{ c }{ v }$ |
et peut tre exprim comme
$n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}$
En d'autres termes,
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
(ID 9776)
Exemples
Si vous observez un arc-en-ciel, vous verrez en r alit qu'il y a plusieurs arcs-en-ciel et que la s quence de couleurs se d place : du bleu au rouge, puis du rouge au bleu, et ainsi de suite.

(ID 1844)
La couleur de la lumi re est associ e sa le fréquence des photons ($\nu$), et il existe une relation directe entre cette fr quence et a fréquence lumineuse ($\epsilon$) :
| $ \epsilon = h \nu $ |
o a constante de Planck ($h$) a une valeur de $6,62\times 10^{-34} , \text{Js}$.
(ID 3341)
Como l'angle de r fraction d pend de la fr quence ou de la longueur d'onde de la lumi re dans le verre, on peut utiliser un prisme pour d composer la lumi re en ses diff rentes couleurs.

On obtient ce que l'on appelle le spectre de la lumi re.
(ID 6972)
L'indice de r fraction, not $n$, est d fini comme le rapport de la vitesse de la lumi re dans le vide, not e $c$, la vitesse de la lumi re dans le milieu, not e $c_m$:
| $ n =\displaystyle\frac{ c }{ v }$ |
(ID 3192)
Le photon est d crit comme une onde, et le fréquence des photons ($\nu$) est li e ERROR:8439 par a surface de la fontaine ($c$), selon la formule suivante :
| $ c = \nu \lambda $ |
Cette formule correspond la relation m canique qui tablit que la vitesse de l'onde est gale la longueur d'onde (distance parcourue) divis e par la p riode d'oscillation, ou inversement proportionnelle la fr quence (l'inverse de la p riode).
(ID 3953)
Si $n$ est l'indice de r fraction dans un milieu et $\lambda$ est la longueur d'onde dans le vide, alors lors de la propagation dans le milieu, la longueur d'onde $\lambda_m$ sera
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
(ID 9776)
Un arc-en-ciel nous montre que la lumi re qui l'illumine se d compose en plusieurs couleurs. En fait, si on l'observe attentivement, on peut voir qu'il existe plusieurs arcs-en-ciel.

Cela s'explique par le fait que chaque goutte d'eau agit comme un petit prisme circulaire, ce qui permet de multiples r fractions et la cr ation de plusieurs arcs-en-ciel.
(ID 1625)
Newton a utilis un prisme pour d composer la lumi re en ses composants, croyant qu'il pouvait identifier un nombre fini de couleurs :

(ID 1682)
Le premier comprendre la structure de la lumi re en tant qu'entit physique fut Sir Isaac Newton.

Sir Isaac Newton
(1643-1727)
Gr ce une exp rience tr s simple, il d montra que la lumi re blanche tait compos e de couleurs. Cependant, il croyait que le nombre de couleurs tait discret, comme le montre son graphique repr sentant ses observations.
(ID 6971)
Les couleurs que nous voyons ne correspondent pas toujours n cessairement la r alit . Nos yeux capturent la lumi re et g n rent des impulsions lectriques en fonction de la quantit de lumi re bleue, rouge et verte que nous percevons. Cependant, l'intensit ne correspond pas toujours aux proportions r elles, ce qui entra ne une perception diff rente de la r alit :

(ID 12676)
ID:(759, 0)
