Utilizador:
Aplicação do teorema de Steiner para um cilindro, eixo $\parallel$
Definição 
Para um cilindro com um eixo paralelo ao eixo do próprio cilindro:
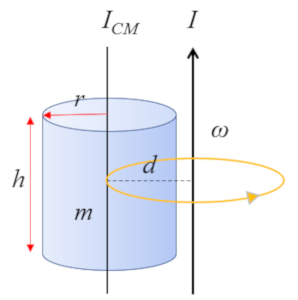
cujo momento de inércia em relação ao centro de massa (CM) é dado por
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
o momento de inércia pode ser calculado usando o teorema de Steiner com a seguinte fórmula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11551, 0)
Aplicação do teorema de Steiner para um cilindro, eixo $\perp$
Imagem
Para um cilindro com um eixo perpendicular ao eixo do próprio cilindro:
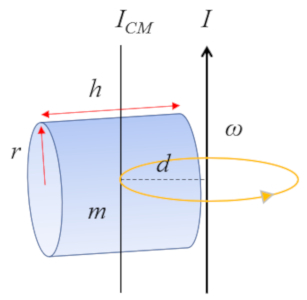
cujo momento de inércia em relação ao centro de massa (CM) é definido como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
o cálculo do momento de inércia pode ser realizado utilizando o teorema de Steiner com a seguinte fórmula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11552, 0)
Aplicação do teorema de Steiner para um paralelepípedo reto
Nota
Para um paralelepípedo reto com eixo paralelo a uma aresta:
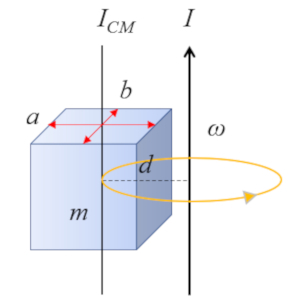
cujo momento de inércia em relação ao centro de massa (CM) é definido como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
o cálculo do momento de inércia pode ser realizado utilizando o teorema de Steiner com a seguinte fórmula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11554, 0)
Aplicação do teorema de Steiner para uma esfera
Citar
Para uma esfera com um eixo a uma distância do centro:
cujo momento de inércia em relação ao centro de massa (CM) é definido como
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
o cálculo do momento de inércia pode ser realizado utilizando o teorema de Steiner com a seguinte fórmula distância centro de massa e eixo $m$, massa corporal $kg$, momento de inércia do centro de massa $kg m^2$ e momento de inércia do eixo que não passa pelo CM $kg m^2$
| $ I = I_{CM} + m d ^2$ |
.
ID:(11553, 0)
Teorema de Steiner
Descrição
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Exemplos
La momento de inércia do eixo que não passa pelo CM ($I$) pode ser calculado usando la momento de inércia do centro de massa ($I_{CM}$) e somando o momento de in rcia de la massa corporal ($m$) como se fosse uma massa pontual em la distância centro de massa e eixo ($d$):
| $ I = I_{CM} + m d ^2$ |
(ID 3688)
Para um cilindro com um eixo paralelo ao eixo do pr prio cilindro:
cujo momento de in rcia em rela o ao centro de massa (CM) dado por
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
o momento de in rcia pode ser calculado usando o teorema de Steiner com a seguinte f rmula
| $ I = I_{CM} + m d ^2$ |
.
(ID 11551)
Para um cilindro com um eixo perpendicular ao eixo do pr prio cilindro:
cujo momento de in rcia em rela o ao centro de massa (CM) definido como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
o c lculo do momento de in rcia pode ser realizado utilizando o teorema de Steiner com a seguinte f rmula
| $ I = I_{CM} + m d ^2$ |
.
(ID 11552)
Para um paralelep pedo reto com eixo paralelo a uma aresta:
cujo momento de in rcia em rela o ao centro de massa (CM) definido como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
o c lculo do momento de in rcia pode ser realizado utilizando o teorema de Steiner com a seguinte f rmula
| $ I = I_{CM} + m d ^2$ |
.
(ID 11554)
Para uma esfera com um eixo a uma dist ncia do centro:
cujo momento de in rcia em rela o ao centro de massa (CM) definido como
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
o c lculo do momento de in rcia pode ser realizado utilizando o teorema de Steiner com a seguinte f rmula distância centro de massa e eixo $m$, massa corporal $kg$, momento de inércia do centro de massa $kg m^2$ e momento de inércia do eixo que não passa pelo CM $kg m^2$
| $ I = I_{CM} + m d ^2$ |
.
(ID 11553)
ID:(1456, 0)